Характеристики вращения тела
- Период вращения — время одного полного оборота. Период вращения T и его частота
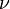связаны соотношением 
.
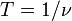· Угловая скорость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:
, а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону.
· Ускоре́ние (обычно обозначается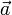 
, в теоретической механике 
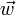) — производная скорости по времени, векторная величина, показывающая, на сколько изменяется вектор скорости точки (тела) при её (его) движении за единицу времени (то есть ускорение учитывает не только изменение величины скорости, но и её направления).
Угол поворота твердого тела. При вращательном движении, в отличие от поступательного, скорости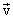 
разных точек тела неодинаковы. Поэтому скорость 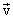какой-либо точки вращающегося тела не может служить характеристикойдвижения всего тела.
Пусть т. О - центр вращения тела, а 
- неподвижная (или мгновенная) ось вращения (рис.2.2).
Положение произвольной т. М тела будем задавать с помощью радиус-вектора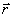 
, проведенного из центра О. Из рисунка видно, что:
,
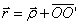где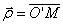 
- радиус-вектор, проведенный в точку дуги окружности, по которой движется т. М. За малое время вектор 
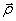поворачивается в плоскости перпендикулярной , на малыйугол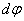 
. На такой же угол поворачивается за время 
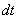радиус-вектор любой другой точки тела, т.к в противном случае расстояние между этими точками должны были измениться. Таким образом, угол поворота характеризует перемещение всего вращающегося тела за малый промежуток времени. Удобно ввести вектор 
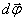элементарного (малого) поворота тела, численно равный 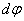и направленный вдоль мгновенной оси так, чтобы из его конца поворот тела был виден происходящим против часовой стрелки.
|
|
Равномерное вращение - вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отчёта может быть как подвижной, так и неподвижной.
Равноускоренное вращение — вращение с постоянным ускорением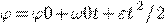 
.
Связь угловых и линейных величин.
Отдельные точки вращающегося тела имеют различные линейные скорости 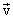. Скорость каждой точки, будучи направлена по касательной к соответствующей окружности, непрерывно изменяет свое направление. Величина скорости 
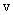определяется скоростью вращения тела 
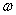и расстоянием R рассматриваемой точки от оси вращения. Пусть за малый промежуток времени 
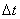тело повернулось на угол 
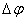(рис 2.4). Точка, находящаяся на расстоянии R от оси проходит при этом путь, равный
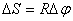
Линейная скорость точки по определению.
| (2.6) |
Найдем линейные ускорения точек вращающегося тела. Нормальное ускорение:
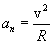
подставляя значение скорости из (2.6), находим: