Св-ва числ рядов.
1) Если  и
и  сходящ, тогда
сходящ, тогда 
2) Если  сход и
сход и  расход, тогда
расход, тогда  расход.
расход.
Док-во (для суммы, от противного):
Пусть  сход. Рассмотрим
сход. Рассмотрим  ряды слевая явл-ся сход, ряд справа расх
ряды слевая явл-ся сход, ряд справа расх  противоречие чтд.
противоречие чтд.
3) Если  сход,
сход,  сход-ся.
сход-ся.
4)  сходится
сходится 

 сход
сход  Справедливо в обе стороны. Данное св-во обозн что на сход-ть не влияет отбрасывание конечн числа первых членов ряда.
Справедливо в обе стороны. Данное св-во обозн что на сход-ть не влияет отбрасывание конечн числа первых членов ряда.
Критерий Коши.

Док-во: 
 исп-я опред Коши т-ма доказана.
исп-я опред Коши т-ма доказана.
Необх усл-е сход.
Если  сход то
сход то 
Док-во:  чтд
чтд
Критерий сходимости полож ряда
Положит ряд сходтися 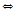 когда последовательность его частичных сумм ограничена сверху.
когда последовательность его частичных сумм ограничена сверху.
Док-во:  ,
,  ,
, 
 по теор-ме о пред монотон послед-ти
по теор-ме о пред монотон послед-ти  сущ-ет и конечен
сущ-ет и конечен  когда эта послед-ть ограничена сверху. Сущ-е этого предела озн-ет сходимость ряда по опред чтд.
когда эта послед-ть ограничена сверху. Сущ-е этого предела озн-ет сходимость ряда по опред чтд.
1ый признак.  и
и  положит ряды,
положит ряды, 
если  сход, то
сход, то  сход
сход
если  расх, то
расх, то  расх
расх
Док-во: по 4му св-ву (на сход не влияет отбрас-е конечно числа членов) 

1)  сход
сход 
 огр-на сверху, те
огр-на сверху, те 
 орг-на сверху
орг-на сверху 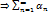 сход
сход
2) Пусть  расход, тогда
расход, тогда  также расходится, тк инчае по 1ой част теор-мы ряд
также расходится, тк инчае по 1ой част теор-мы ряд  должен сходится, что противоречит условию.
должен сходится, что противоречит условию.
Признак Даламбера.
Пусть  строго полож,
строго полож, 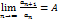
1) Если  ряд сход
ряд сход
2) Если  ряд расх
ряд расх
3) Если  признак непременим
признак непременим
Док-во:


1) 
 выберем
выберем 
 - геом ряд
- геом ряд  ряд сход
ряд сход  по 3ему призн сравн-я исх ряд сход.
по 3ему призн сравн-я исх ряд сход.
2)  выберем
выберем 
 - геом ряд
- геом ряд  ряд расх
ряд расх  по 3ему призн сравн-я исх ряд расх.
по 3ему призн сравн-я исх ряд расх.
3) 
 расх,
расх, 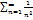 сход,
сход, 


 неопред, чтд.
неопред, чтд.
Признак Коши.
Пусть  положит ряд и
положит ряд и 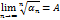
1) Если  ряд сход
ряд сход
2) Если  ряд расх
ряд расх
3) Если  неопред
неопред
Док-во:


1) 
 выберем
выберем 

 геом ряд,
геом ряд, 
 сходится
сходится  по 1му признаку сравнения исх ряд сход
по 1му признаку сравнения исх ряд сход
2) 
 выберем
выберем 

 тк
тк  для
для  то
то 
 не выполнено необх усл-е, ряд расх
не выполнено необх усл-е, ряд расх
3) 
 расх,
расх, 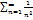 сход,
сход, 
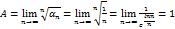

 неопред, чтд.
неопред, чтд.
Мажорантный признак:  равномерно сходится на
равномерно сходится на  если для него на этом отрезке
если для него на этом отрезке  сход-ся мажорирующ ряд
сход-ся мажорирующ ряд 
Док-во:  оценим
оценим 
 ряд сходится равномерно чтд.
ряд сходится равномерно чтд.
Первая теор-а Абеля
Если ряд  сход в некоторой тчке
сход в некоторой тчке  то он сход в
то он сход в  . Если ряд расх в тчке
. Если ряд расх в тчке  то он расх
то он расх 
Док-во:  сход по усл-ю
сход по усл-ю 

 {
{  } сход и огр-на
} сход и огр-на 
Исх ряд абс сходится для  по призн сравнения
по призн сравнения
Исх ряд рясходится для  по призн сравнения (противоречие усл-ю теор-ы в случае если бы он сходился). Т-ма доказана.
по призн сравнения (противоречие усл-ю теор-ы в случае если бы он сходился). Т-ма доказана.
Вычисл R т-ма 1
Если  , тогда если
, тогда если
1) 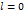 то
то 
2)  то
то 
3)  то
то 
Док-во: рассмотрим  исп-я призн Даламбера
исп-я призн Даламбера 
1) 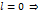 для
для 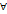 конечн
конечн  ,
,  Ряд сход абс на всей прямой
Ряд сход абс на всей прямой 

2)  для
для 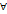
 ,
,  Ряд сход во всех тчках кроме
Ряд сход во всех тчках кроме 
3) 
 сход-ть для
сход-ть для 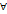

 для этих рядов будет сх-ся абс
для этих рядов будет сх-ся абс 

Вторая теор-а Абеля
Ряд  сход равномерно на
сход равномерно на 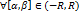
Док-во: 
 сход абс и
сход абс и 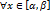 имеет место неравенство
имеет место неравенство  по призн Вейерштрасса
по призн Вейерштрасса  сход равномерн на
сход равномерн на  чтд.
чтд.
Непрерывность суммы
Сумму степ ряда  непр-я ф-я в
непр-я ф-я в 
Док-во:  Расм-м
Расм-м  . По 2ой теор-ме Абеля и теор-ме о непр-ти функц рядов непр-на на
. По 2ой теор-ме Абеля и теор-ме о непр-ти функц рядов непр-на на 
 непр-ть в тчке
непр-ть в тчке  чтд
чтд
Дифф-ть суммы
 явл-ся ф-ей дифф-ой на
явл-ся ф-ей дифф-ой на  , причем
, причем  и
и  имеет
имеет  такой же как и
такой же как и  исх ряда
исх ряда
Док-во:
Расм-м  . По теор-е о дифф-ти функц ряда
. По теор-е о дифф-ти функц ряда 
 дифф-ма и
дифф-ма и 

Интегр суммы
 явл-ся ф-ей интегр-ой на
явл-ся ф-ей интегр-ой на  , причем
, причем  и
и  имеет
имеет  такой же как и
такой же как и  исх ряда
исх ряда
Док-во: пусть  , расм-м
, расм-м  . По 2ой теор-ме Абеля и теор-ме о интегр-ти функц рядов степ ряд можно интегр-ть почленно.
. По 2ой теор-ме Абеля и теор-ме о интегр-ти функц рядов степ ряд можно интегр-ть почленно.
Равенство 
Т-ма единственности
Если  на
на  разлагается в степ ряд, то это разложение единств
разлагается в степ ряд, то это разложение единств
Док-во: 
 (и при
(и при 

 , исп-я т-му о дифф степ ряда, данное равенство можно дифф-ать и полученое рав-во
, исп-я т-му о дифф степ ряда, данное равенство можно дифф-ать и полученое рав-во  справедливо для
справедливо для 
 исп-я з-е к теор-ме дифф-ти получаем что степ ряд это
исп-я з-е к теор-ме дифф-ти получаем что степ ряд это  дифф-я ф-я
дифф-я ф-я  это равенство можно дифф-ать сколь угодно раз, и полученное равенство справедливо для
это равенство можно дифф-ать сколь угодно раз, и полученное равенство справедливо для  . В общ виде
. В общ виде 
 все члены степ ряда опред-ся однозначно
все члены степ ряда опред-ся однозначно  разложение единств чтд
разложение единств чтд
З-е: из док-ва теор-мы следует что если ф-я разлагается в степ ряд это будет ряд Тейлора 
Необх и дост-е усл-е разлож ф-ии в степ ряд
 на
на  разлаг в степ ряд
разлаг в степ ряд 
 беск дифф-ма на
беск дифф-ма на  и ост член в ф-ле Тейлора
и ост член в ф-ле Тейлора  при
при  для
для 
Док-во: Необх; тк  разлаг в степ ряд, то в силу з-я к теор-е о дифф-ти степ ряда
разлаг в степ ряд, то в силу з-я к теор-е о дифф-ти степ ряда  явл-ся
явл-ся  дифф-ой на
дифф-ой на  как сумма ряда.
как сумма ряда.

 чтд.
чтд.
Дост-ть; тк  явл-ся
явл-ся  дифф-ой ф-ей то можно записать ф-лу Тейлора
дифф-ой ф-ей то можно записать ф-лу Тейлора  причем
причем 


Частичн сумма степ ряда 
Рассм-м 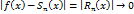 при
при  ,
, 
 т.е ряд сход и его сумма
т.е ряд сход и его сумма  чтд
чтд