Лабораторная работа №
Однофакторный корреляционный и регрессионный анализ (4 часа)
Цель работы
1. Изучить методику проведения однофакторного корреляционного и регрессионного анализа.
2. Сформировать практические навыки проведения однофакторного корреляционного и регрессионного анализа.
3. Построить уравнение регрессии, определить коэффициенты регрессии, коэффициент корреляции, коэффициент детерминации.
4. Оценить значимость коэффициентов регрессии и уравнения регрессии.
Краткая теория
Связь между явлениями классифицируется по ряду признаков, которые делятся на два класса: факторные, вызывающие измененияявлений, и результативные, изменяющиеся под влиянием факторных. Связи между явлениями и признаками классифицируются по степени тесноты, направлению, аналитическому выражению и количеству факторов, действующих на результативный признак.
Рассматривается выборка двух взаимосвязанных дискретных случайных величин X и Y. Пара  , где
, где 
 соответствует i -й точке (i -му опыту). Здесь n – объем парной выборки.
соответствует i -й точке (i -му опыту). Здесь n – объем парной выборки.
Для удобства последующего использования табличные (опытные) данные моделируют некоторой функцией, которую называют уравнением регрессии:
 .
.
Процедура построения регрессионной (статистической) модели предусматривает, во-первых, выбор функции  .
.
В качестве функции чаще всего используют полином:
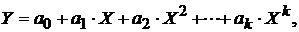 (5.1)
(5.1)
где  − коэффициенты регрессии
− коэффициенты регрессии  ; k − порядок полинома.
; k − порядок полинома.
На втором этапе построения модели определяют коэффициенты регрессии  . Это осуществляется путем аппроксимации опытных точек.
. Это осуществляется путем аппроксимации опытных точек.
Уравнение регрессии позволяет вычислить ожидаемое значение функции Y для опытных значений 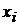 :
:
 (5.2)
(5.2)
Разность между опытным значением  и ожидаемым значением
и ожидаемым значением 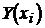 составляет ошибку или погрешность функции:
составляет ошибку или погрешность функции:
 (5.3)
(5.3)
Аппроксимация может быть произведена при разных требованиях к величине  . Наиболее распространенным является требование мини-мизации суммы квадратов отклонений опытных точек от линии регрессии. Это требование называют принципом Лежандра, согласно которому коэффициенты регрессии
. Наиболее распространенным является требование мини-мизации суммы квадратов отклонений опытных точек от линии регрессии. Это требование называют принципом Лежандра, согласно которому коэффициенты регрессии  должны быть подобраны так, чтобы сумма:
должны быть подобраны так, чтобы сумма:
 (5.4)
(5.4)
принимала минимальное значение.
Метод определения коэффициентов регрессии по принципу Лежандра называют методом наименьших квадратов.
Искомые коэффициенты регрессии находятся из решения системы уравнений:

или

Отсюда получается система нормальных уравнений:
 (5.5)
(5.5)
В простейшем случае k = 1, то есть полинома первой степени, уравнение регрессии принимает вид:
 (5.6)
(5.6)
Система (5.5) также упрощается:
 (5.7)
(5.7)
Уравнение (5.6) с коэффициентами регрессии учитывает погрешность функции и не учитывает погрешность фактора. Его называют уравнением прямой регрессии.
 Y
Y





 |  |





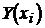














 | |||
 |
0  X
X
Рис. 5.1. Аппроксимация опытных данных линейным уравнением прямой регрессии
Решим систему (5.7) двух уравнений с двумя неизвестными а 0 и а 1:
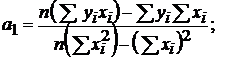 (5.8)
(5.8)
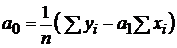 . (5.9)
. (5.9)
Направление связи между переменными определяется на основании знаков (отрицательный или положительный) коэффициента регрессии (коэффициента а 1).
Если знак при коэффициенте регрессии − положительный, связь зависимой переменной с независимой будет положительной. Если знак при коэффициенте регрессии − отрицательный, связь зависимой переменной с независимой является отрицательной (обратной).
Для анализа общего качества уравнения регрессии используют обычно множественный коэффициент детерминации R 2, называемый также квадратом коэффициента множественной корреляции R. R 2 (мера определенности) всегда находится в пределах интервала [0; 1].
Если значение R 2 близко к единице, это означает, что построенная модель объясняет почти всю изменчивость соответствующих переменных. И наоборот, значение R-квадрата, близкое к нулю, означает плохое качество построенной модели.
Коэффициент детерминации R 2 показывает, на сколько процентов  найденная функция регрессии описывает связь между исходными значениями факторов X и Y:
найденная функция регрессии описывает связь между исходными значениями факторов X и Y:

где  – объясненная вариация;
– объясненная вариация;  – общая вариация.
– общая вариация.
Соответственно, величина 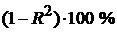 показывает, сколько процен-тов вариации параметра Y обусловлены факторами, не включенными в регрес-сионную модель. При высоком
показывает, сколько процен-тов вариации параметра Y обусловлены факторами, не включенными в регрес-сионную модель. При высоком  значении коэффициента детерми-нации можно делать прогноз
значении коэффициента детерми-нации можно делать прогноз  для конкретного значения
для конкретного значения  .
.
Множественный R − коэффициент множественной корреляции R − выражает степень зависимости независимых переменных (X) и зависимой переменной (Y) и равен квадратному корню из коэффициента детерминации, эта величина принимает значения в интервале от нуля до единицы. В простом линейном регрессионном анализе множественный R равен коэффициенту корреляции Пирсона, который вычисляется по формуле:
 (5.10)
(5.10)
Коэффициент корреляции может принимать значения в пределах  . Функциональной связи отвечает значение
. Функциональной связи отвечает значение  . При r = 0 величины X и Y не зависят друг от друга. При
. При r = 0 величины X и Y не зависят друг от друга. При  связь является вероятностной.
связь является вероятностной.
Интерпретация значений r представлена в табл. 5.1, 5.2.
Таблица 5.1
Оценка линейного коэффициента корреляции r по характеру связи
| Значение линейного коэффициента связи | Характер связи | Интерпретация связи |
| r = 0 | Отсутствует | – |
| 0 < r < 1 | Вероятностная, прямая | С увеличением X увеличивается Y |
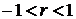
| Вероятностная, обратная | С увеличением X уменьшается Y и наоборот |
| r = +1 | Функциональная, прямая | Каждому значению факторного признака строго соответствует одно значение функции, с увеличением X увеличивается Y |
| r = -1 | Функциональная, обратная | Каждому значению факторного признака строго соответствует одно значение функции, с увеличением X уменьшается Y и наоборот |
Таблица 5. 2
Оценка коэффициента корреляции r по степени тесноты связи
| Значение линейного коэффициента связи | Характер связи |
| До ê ± 0,3 ê | Практически отсутствует |
| ê ± 0,3 ê – ê ± ê0,5 ê | Слабая |
| ê ± 0,5 ê– ê ± 0,7 ê | Умеренная |
| ê ± 0,7 ê– ê ± 1,0 ê | Сильная |
Для практического использования моделей регрессии очень важна их адекватность, т.е. соответствие фактическим статистическим данным. Значимость коэффициентов простой линейной регрессии осуществляется с помощью t -критерия Стьюдента. При этом вычисляют расчетные значения t -критерия:
– для параметра a 0  ; (5.11)
; (5.11)
– для параметра a 1 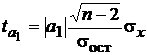 , (5.12)
, (5.12)
где n – объем выборки;
 − среднее квадратическое отклонение результативного признака y от выравненных значений
− среднее квадратическое отклонение результативного признака y от выравненных значений  ;
;
 − среднее квадратическое отклонение факторного признака x от общей средней
− среднее квадратическое отклонение факторного признака x от общей средней  .
.
Вычисленные по формулам (5.11) и (5.12) значения, сравнивают с критическими  , которые определяются по таблице Стьюдента (табл. 5.3) с учетом принятого уровня значимости
, которые определяются по таблице Стьюдента (табл. 5.3) с учетом принятого уровня значимости  и числом степеней свободы вариации
и числом степеней свободы вариации  (m − число факторных признаков в уравнении). Обычно в социально-экономических расчетах уровень значимости
(m − число факторных признаков в уравнении). Обычно в социально-экономических расчетах уровень значимости  принимается равным 0,05. При
принимается равным 0,05. При  параметр является значимым (существенным). Если в уравнении все коэффициенты регрессии значимы, то данное уравнение признают окончательным и применяют в качестве модели изучаемого показателя для последующего анализа.
параметр является значимым (существенным). Если в уравнении все коэффициенты регрессии значимы, то данное уравнение признают окончательным и применяют в качестве модели изучаемого показателя для последующего анализа.
Таблица 5.3
Квантили распределения Стьюдента 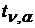
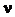
| Уровни значимости a | |||
| 0,20 | 0,10 | 0,05 | 0,01 | |
| 3,08 | 6,31 | 12,71 | 63,66 | |
| 1,89 | 2,92 | 4,30 | 9,93 | |
| 1,64 | 2,35 | 3,18 | 5,84 | |
| 1,53 | 2,13 | 2,78 | 4,60 | |
| 1,48 | 2,02 | 2,57 | 4,03 | |
| 1,44 | 1,94 | 2,45 | 3,71 | |
| 1,42 | 1,90 | 2,37 | 3,50 | |
| 1,40 | 1,86 | 2,31 | 3,36 | |
| 1,38 | 1,83 | 2,26 | 3,25 | |
| 1,37 | 1,81 | 2,23 | 3,17 | |
| 1,34 | 1,75 | 2,13 | 2,95 | |
| 1,33 | 1,73 | 2,09 | 2,85 | |
| 1,31 | 1,70 | 2,04 | 2,75 | |
| 1,30 | 1,68 | 2,02 | 2,70 |
Проверка значимости уравнения регрессии производится на основе вычисления F- критерия Фишера:
 ,
,
где 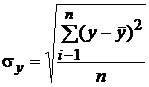 – среднее квадратическое отклонение результа-тивного признака y от общей средней
– среднее квадратическое отклонение результа-тивного признака y от общей средней  .
.
Полученное значение – критерий F расч сравнивают с критическим (табличным) для принятого уровня значимости a и чисел степеней свободы  и
и  . Величины F табл при различных значениях
. Величины F табл при различных значениях  ,
,  и уровнях значимости a приведены в табл. 5.4. Уравнение регрессии значимо, если F расч > F табл.
и уровнях значимости a приведены в табл. 5.4. Уравнение регрессии значимо, если F расч > F табл.
Это означает, что доля вариации, обусловленная регрессией, намного превышает случайную ошибку. Принято считать, что уравнение регрессии пригодно для практического использования в том случае, если F расч превышает табличное не менее чем в 4 раза.
Таблица 5.4
Значения  по распределению Фишера
по распределению Фишера
при уровне значимости  = 0,05
= 0,05
  
| ||||||
| 161,4 | 199,5 | 215,7 | 224,6 | 230,2 | 234,0 | |
| 18,51 | 19,00 | 19,16 | 19,25 | 19,30 | 19,33 | |
| 10,13 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | |
| 7,71 | 6,94 | 6,59 | 6,39 | 6,26 | 6,16 | |
| 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4,95 | |
| 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | |
| 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | |
| 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | |
| 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,37 | |
| 4,96 | 4,10 | 3,71 | 3,48 | 3,33 | 3,22 | |
| 4,84 | 3,98 | 3,59 | 3,36 | 3,20 | 3,09 | |
| 4,75 | 3,88 | 3,49 | 3,26 | 3,11 | 3,00 | |
| 4,67 | 3,80 | 3,41 | 3,18 | 3,02 | 2,92 | |
| 4,60 | 3,74 | 3,34 | 3,11 | 2,96 | 2,85 |
Методические рекомендации