· Находим отрезки, отсекаемые плоскостью на координатных осях, измеряя их в осевых единицах.
· Берем обратные значения этих величин.
· Приводим отношение полученных чисел к отношению трех наименьших целых чисел.
· Полученные три числа заключаем в круглые скобки.
Если плоскость пересекает кристаллографическую ось в отрицательном направлении, над соответствующим индексом сверху ставится знак "минус". Если плоскость параллельна какой-либо координатной оси, то в символе плоскости индекс, соответствующий этой оси, равен нулю.
Иногда индексы плоскости записывают в фигурных скобках {hkl}. Эта запись означает символ совокупности идентичных плоскостей. Такие плоскости проходят через одинаковые узлы в пространственной решетке, симметрично расположены в пространстве и характеризуются одинаковым межплоскостным расстоянием.
Кристаллографические индексы узла, кристаллографические индексы направления.
Кристаллографические индексы узла — это его координаты, взятые в долях осевых единиц и записанные в сдвоенных квадратных скобках. Символ узла имеет вид [[ uvw ]].
Кристаллографические индексы направления ( индексы Вейса)
В кристалле, где все параллельные направления идентичны друг другу, направление, проходящее через начало координат, характеризует все данное семейство параллельных направлений.
Положение в пространстве направления, проходящего через начало координат, определяется координатами любого узла, лежащего на этом направлении.
Координаты любого узла, принадлежащего направлению, выраженные в долях осевых единиц и приведенные к отношению трех целых наименьших чисел, и есть кристаллографические индексы направления. Они обозначаются целыми числам u, v, w и записываются слитно в квадратных скобках [ uvw ].
Порядок нахождения индексов направления
1. Из семейства параллельных направлений выбрать такое, которое проходит через начало координат, или перенести данное направление параллельно самому себе в начало координат, или перенести начало координат в узел, лежащий на данном направлении.
2. Найти координаты любого узла, принадлежащего данному направлению, выразив их в осевых единицах.
3. Взять отношение координат узла и привести его к отношению трех целых наименьших чисел.
4. Полученные три числа заключить в квадратные скобки.
Понятие о кристаллическом и полярном комплексе.
Метод кристаллографических проекций основан на одной из характерных особенностей кристаллов — законе постоянства углов: углы между определенными гранями и ребрами кристалла всегда постоянны.
Так, когда кристалл растет, меняются размеры граней, их форма, но углы остаются неизменными. Поэтому в кристалле можно перенести все ребра и грани параллельно самим себе в одну точку пространства; угловые соотношения при этом сохраняется.
Такая совокупность плоскостей и направлений, параллельных плоскостям и направлениям в кристалле и проходящая через одну точку, получила название кристаллического комплекса, а сама точка называется центром комплекса. При построении кристаллографических проекций кристалл всегда заменяют кристаллическим комплексом.
Чаще рассматривают не кристаллический комплекс, а полярный.
Полярный комплекс, получают из кристаллического путем замены плоскостей нормалями к ним, а направлений - перпендикулярными к ним плоскостями.
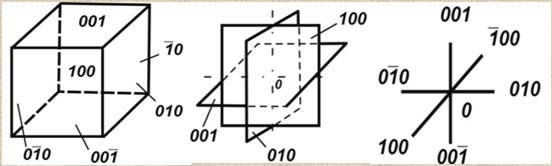
Куб (а), его кристаллический (б) и
Полярный комплекс (в)
Понятие о симметрии. Элементы симметрии. Понятие о классе симметрии.
Под симметрией понимают свойство тел или геометрических фигур совмещать отдельные части друг с другом при некоторых симметрических преобразованиях. Геометрические образы, с помощью которых задаются и осуществляются симметрические преобразования, называют элементами симметрии.
Континуум — означает непрерывный, сплошной. Все точки в такой среде совершенно одинаковы.
Элементы симметрии
В кристаллических многогранниках встречаются простые элементы симметрии (центр симметрии, плоскость симметрии, поворотная ось) и сложный элемент симметрии (инверсионная ось).
Центр симметрии (С или I) — особая точка внутри фигуры, при отражении в которой любая точка фигуры имеет эквивалентную себе, то есть обе точки (например, пара вершин) расположены на одной прямой, проходящей через центр симметрии, и равноудалены от него.
Плоскость симметрии (P или m)— это такая плоскость, которая делит фигуру на две части, расположенные друг относительно друга как предмет и его зеркальное отражение, то есть на две зеркально равные части. Графически плоскость симметрии обозначается сплошной линией. У фигуры может быть одна или несколько плоскостей симметрии, и все они пересекаются друг с другом. В кубе имеется девять плоскостей симметрии.
Поворотная ось (L) — это такая прямая, при повороте вокруг которой на некоторый определенный угол a фигура совмещается сама с собой. Величина угла поворота a определяет порядок поворотной оси n, который показывает, сколько раз фигура совместится сама с собой при полном обороте вокруг этой оси на 360 °: n = 360/a
В изолированных геометрических фигурах возможны оси симметрии любых порядков, но в кристаллических многогранниках порядок оси ограничен, он может иметь только следующие значения: n = 1, 2, 3, 4, 6. В кристаллических многогранниках невозможны оси симметрии пятого и выше шестого порядков. Это вытекает из принципа непрерывности кристаллической среды.
Инверсионная ось — позволяет совмещать равные части фигуры путём двойной операции — поворота на определённый угол, задаваемый порядком оси, и отражения в точке этой оси.
Класс симметрии — полный набор элементов симметрии, присущих данному кристаллу.
Число сочетаний элементов симметрии друг с другом в кристаллах строго ограничено.
Сщуствует 32 класса симметрии.