Контрольная работа № 3
Дифференциальные уравнения и системы
Операционное исчисление. Ряды
Требования к оформлению контрольных работ
В контрольную работу включены шесть заданий по темам:
– дифференциальные уравнения и системы;
– операционное исчисление;
– ряды.
Контрольная работа должна выполняться студентом в соответствии с номером варианта, который определяется двумя последними цифрами номера зачетной книжки студента.
При оформлении контрольной работы необходимо учитывать следующие требования:
1) на титульном листе указать номер варианта;
2) контрольные работы оформлять, оставляя поля для замечаний преподавателя;
3) условия задач необходимо записывать полностью. Если задание имеет общую формулировку, его условие необходимо переписать, подставляя числовые значения, соответствующие номеру варианта;
4) решения заданий оформлять аккуратно, приводить достаточное количество пояснений, делать необходимые рисунки.
Контрольную работу необходимо сдать за 10 дней до начала экзаменационной сессии, в противном случае студент не будет допущен до зачета или экзамена.
Решение типового варианта
Задача 1. а) Найти общее решение дифференциального уравнения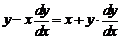 
,
б) найти общее решение дифференциального уравнения 
.
Решение. а) Из данного уравнения находим 
:
.
Исходное уравнение является однородным уравнением 1-го порядка. Решаем его с помощью подстановки 
. Находим:
, 
, 
, 
, 
, 
.
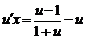Получили уравнение с разделяющимися переменными. Решаем его:
, 
, 
, 
, 
, т. е. нашли общий интеграл исходного уравнения.
б) преобразуем уравнение для того, чтобы определить его тип. Получим
.
Данное уравнение является уравнением Бернулли. Решаем его с помощью подстановки 
. Тогда
, 
, 
. (1)
Находим 
из условия 
, которое является дифференциальным уравнением с разделяющимися переменными: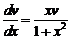 
, 
, 
,
, 
.
Полученное выражение для подставляем в уравнение (1):
, 
, 
, 
,
= 
= 
= 
=
= 
= 
Следовательно, 
,
.
Окончательно находим, что общее решение исходного уравнения определяется формулой
.
Задача 2. Найти общее решение дифференциального уравнения
.
Решение. Характеристическое уравнение 
имеет мнимые корни: 
. Общее решение соответствующего однородного уравнения определяется формулой 
. Рассмотрим правую часть уравнения 
. Она имеет вид 
, где 
. Частное решение ищем в виде 
, где 
– полином той же степени, что и 
, но в общем виде, 
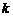означает, сколько раз число 
встретилось среди корней характеристиче5ского уравнения. В нашем случае 
. Находим
, 
.
Подставим выражение 
, 
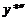в исходное уравнение и из полученного тождества, сравнивая коэффициенты при одинаковых степенях 
,
,
найдём 
. Тогда 
. Общее решение исходного уравнения имеет вид
.
Задача 3. Решить систему дифференциальных уравнений 
Решение. Дифференцируем первое уравнение данной системы. Получаем: 
. Затем заменяем в последнем уравнении 
его выражением из второго уравнения данной системы: 
. В последующем уравнении 
заменяем выражением 
, найденным из первого уравнения системы. В итоге приходим к дифференциальному уравнению второго порядка относительно неизвестной функции 
: 
, 
. Решаем последнее уравнение:
, 
, 
.
Отсюда находим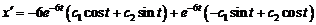 
.
Подставляя полученные выражения для и 
в , имеем:
.
Следовательно, искомым решением являются функции:
, 
.
Задача 3. Решить операторным методом дифференциальное уравнение
.
Решение. Т.к. 
и по условию 
, то операторное уравнение имеет вид 
, и, значит, операторное решение 
. Разложим правую часть на элементарные дроби 
. Переходя к оригиналам, получим решение в виде 
.
Ряды
Числовым рядом называется выражение
, (1)
где 
– числовая последовательность.
Необходимый признак сходимости ряда: если ряд (1) сходится, то его общий член стремится к нулю, т.е. 
.
Следствие. Если общий член ряда (1) не стремится к нулю, то ряд (1) расходится.
Простейшие ряды:
1) Сумма геометрической прогрессии со знаменателем 
, т.е. 
Этот ряд сходится, если 
. Если 
, то данный ряд расходится.
2) Обобщенный гармонический ряд 
. Этот ряд сходится, если 
и расходится, если 
. При 
получаем ряд 
, который называется гармоническим.