Числовой ряд  с положительными членами называется числовым знакоположительным рядом.
с положительными членами называется числовым знакоположительным рядом.
Рассмотрим числовые ряды
 (2)
(2)
и
 . (3)
. (3)
Первый признак сравнения. Если при 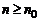 для рядов (2) и (3) выполнено условие
для рядов (2) и (3) выполнено условие 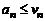 и ряд (3) сходится, то сходится и ряд (2). Если же ряд (3) расходится, то расходится и ряд (3).
и ряд (3) сходится, то сходится и ряд (2). Если же ряд (3) расходится, то расходится и ряд (3).
Второй признак сравнения. Если существует конечный и отличный от нуля предел
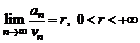 ,
,
то ряды (2) и (3) сходятся и расходятся одновременно.
Признак Даламбера. Если для ряда (2) существует предел 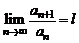 , то при
, то при  ряд (2) сходится, а при
ряд (2) сходится, а при 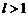 расходится.
расходится.
Признак Коши. Если для ряда (2) существует предел 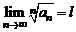 , то при
, то при  ряд (2) сходится, а при
ряд (2) сходится, а при 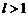 расходится.
расходится.
Если пределы в признаках Коши и Даламбера равны единице, то необходимо дополнительное исследование сходимости.
Интегральный признак Коши-Маклорена. Если члены ряда (2) не возрастают (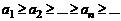 ) и существует неотрицательная невозрастающая функция
) и существует неотрицательная невозрастающая функция  при
при  , то ряд (2) сходится или расходится вместе с интегралом
, то ряд (2) сходится или расходится вместе с интегралом 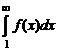 .
.
Для того, чтобы исследовать на сходимость ряд  , где
, где 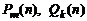 – многочлены степени
– многочлены степени 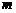 и
и 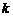 соответственно, нужно составить обобщенный гармонический ряд
соответственно, нужно составить обобщенный гармонический ряд 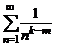 . При этом целесообразно применять второй признак сравнения.
. При этом целесообразно применять второй признак сравнения.
Признаки сходимости числовых знакочередующихся рядов
Числовой ряд, у которого любые два соседних члена имеют разные знаки, т.е.
 , (4)
, (4)
в котором 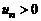 называется знакочередующимся рядом. В случае, если сходится ряд, составленный из модулей членов ряда (4), т.е. ряд
называется знакочередующимся рядом. В случае, если сходится ряд, составленный из модулей членов ряда (4), т.е. ряд  , то ряд (4) называется абсолютно сходящимся. Если же ряд (4) сходится, а
, то ряд (4) называется абсолютно сходящимся. Если же ряд (4) сходится, а  расходится, то ряд (4) называется сходящимся условно.
расходится, то ряд (4) называется сходящимся условно.
Признак Лейбница. Знакочередующийся ряд (4) сходится, если выполняются условия:
1)  ,
,
2)  .
.
Степенные ряды
Степенным рядом называется выражение вида
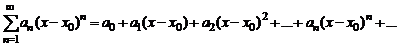 , (5)
, (5)
где  – постоянные, называемые коэффициентами ряда.
– постоянные, называемые коэффициентами ряда.
Если 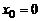 , то степенной ряд принимает вид
, то степенной ряд принимает вид
 (6)
(6)
Радиусом сходимости ряда (6) называется величина  (число) такая, что при всех
(число) такая, что при всех 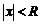 ряд сходится, а при всех
ряд сходится, а при всех 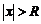 расходится. Интервал
расходится. Интервал 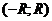 в этом случае называется интервалом сходимости ряда (6). На концах интервала сходимости ряд может как сходится, так и расходится (это нужно исследовать).
в этом случае называется интервалом сходимости ряда (6). На концах интервала сходимости ряд может как сходится, так и расходится (это нужно исследовать).
Если ряд (6) сходится на всей числовой оси, то  , если он сходится только для
, если он сходится только для  , то
, то  .
.
Если при  ряд (5) сходится, а при всех
ряд (5) сходится, а при всех 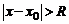 расходится, то
расходится, то  – радиус сходимости, а интервал
– радиус сходимости, а интервал  – интервал сходимости.
– интервал сходимости.
Радиус сходимости можно вычислять по одной из формул:
 или
или  .
.
Задача 5. Найти интервалы сходимости следующих степенных рядов:
а)  ; б)
; б) 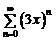 ; в)
; в) 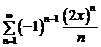
и исследовать сходимость на концах интервала сходимости.
Решение. а) Воспользуемся признаком Даламбера. Так как признак Даламбера применим для рядов с положительными членами, то будем исследовать ряд из абсолютных величин членов данного ряда:
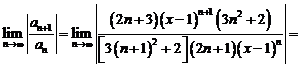
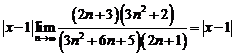 .
.
Ряд сходится, если 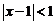 , т. е. если
, т. е. если  ,
, 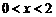 . Значит, радиус сходимости
. Значит, радиус сходимости  ; интервал сходимости:
; интервал сходимости: 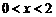 .
.
Исследуем сходимость ряда на концах полученного интервала, т.е. в точках 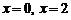 .
.
В точке  исходный ряд имеет вид
исходный ряд имеет вид 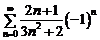 . Это числовой, знакочередующийся ряд. Проверим выполнение условий признака Лейбница:
. Это числовой, знакочередующийся ряд. Проверим выполнение условий признака Лейбница:
1) 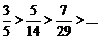 ; 2)
; 2) 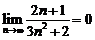 . Они выполняются. Исследуем сходимость соответствующего знакоположительного ряда
. Они выполняются. Исследуем сходимость соответствующего знакоположительного ряда 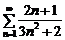 . Подберем обобщенный гармонический ряд
. Подберем обобщенный гармонический ряд  . Этот ряд расходящийся. По предельному признаку сравнения
. Этот ряд расходящийся. По предельному признаку сравнения 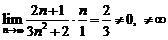 . Значит ряд
. Значит ряд 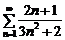 также расходится. Таким образом, ряд
также расходится. Таким образом, ряд 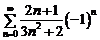 сходится условно.
сходится условно.
При 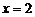 исходный ряд имеет вид
исходный ряд имеет вид 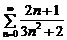 . Это числовой, знакоположительный ряд. Как показано выше он расходится.
. Это числовой, знакоположительный ряд. Как показано выше он расходится.
Таким образом, радиус сходимости ряда  ; интервал сходимости:
; интервал сходимости:  .
.
б). Применим признак Коши: 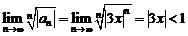 ,
, 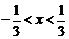 . Исследуем сходимость ряда на концах интервала сходимости, т.е. в точках
. Исследуем сходимость ряда на концах интервала сходимости, т.е. в точках 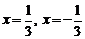 . При
. При  исходный ряд имеет вид
исходный ряд имеет вид  . Это расходящийся ряд, поскольку не выполняется необходимое условие сходимости числового ряда, т.е.
. Это расходящийся ряд, поскольку не выполняется необходимое условие сходимости числового ряда, т.е. 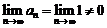 .
.
При 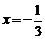 исходный ряд имеет вид
исходный ряд имеет вид  . Это расходящийся ряд, поскольку не выполняется второе условие признака Лейбница, т.е.
. Это расходящийся ряд, поскольку не выполняется второе условие признака Лейбница, т.е.  .
.
Ответ: радиус сходимости: 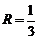 ; интервал сходимости:
; интервал сходимости: 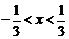 .
.
в) Применим признак Даламбера: 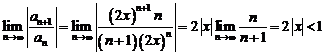 , тогда
, тогда 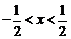 . Исследуем сходимость ряда на концах интервала сходимости, т.е. в точках
. Исследуем сходимость ряда на концах интервала сходимости, т.е. в точках 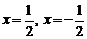 . При
. При 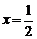 исходный ряд имеет вид
исходный ряд имеет вид 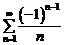 . Это ряд, сходящийся условно, поскольку выполняются условия признака Лейбница, но расходится ряд
. Это ряд, сходящийся условно, поскольку выполняются условия признака Лейбница, но расходится ряд  составленный из абсолютных величин ряда
составленный из абсолютных величин ряда 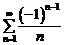 .
.
При  исходный ряд имеет вид
исходный ряд имеет вид 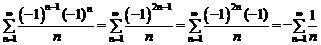 . Это расходящийся гармонический ряд.
. Это расходящийся гармонический ряд.
Ответ: радиус сходимости: 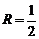 ; интервал сходимости
; интервал сходимости  .
.
Замечание. Степенной ряд может как сходиться, так и расходиться на концах интервала сходимости. В этих граничных точках требуется дополнительное исследование. При исследовании степенных рядов на концах интервала сходимости можно придти к рядам вида:
а) 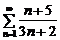 ; б)
; б) 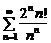 ; в)
; в) 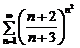 ; г)
; г) 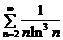 ; д)
; д)  , е)
, е)  .
.
Решение. а) Это числовой знакоположительный ряд. Общий член ряда  . Вычислим предел
. Вычислим предел  . Так как необходимый признак сходимости ряда не выполняется, то ряд расходится.
. Так как необходимый признак сходимости ряда не выполняется, то ряд расходится.
б) Это числовой знакоположительный ряд. Применим признак Даламбера. Так как 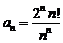 ,
, 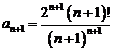 , то
, то 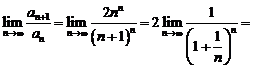
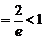 . По признаку Даламбера ряд сходится.
. По признаку Даламбера ряд сходится.
в) Это числовой знакоположительный ряд. Применим признак Коши. Имеем: 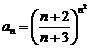 ,
, 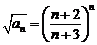 . Следовательно,
. Следовательно, 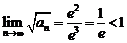 , поэтому ряд сходится.
, поэтому ряд сходится.
г) Это числовой знакоположительный ряд. Применим интегральный признак Коши. Члены данного ряда положительны и убывают, поэтому в качестве функции  , о которой идет речь в интегральном признаке, возьмем функцию
, о которой идет речь в интегральном признаке, возьмем функцию 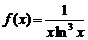 ,
, 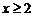 , т.к.
, т.к. 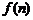
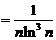 . Т.к.
. Т.к. 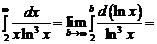 =
= 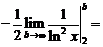
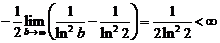 , т.е. интеграл сходится, а поэтому и данный ряд сходится.
, т.е. интеграл сходится, а поэтому и данный ряд сходится.
д) Это числовой знакоположительный ряд. Применим предельный признак сравнения. Т.к. степень числителя равна 2, а степень знаменателя равна 4, то составим обобщенный гармонический ряд 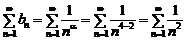 .
.
Поскольку  , то подобранный ряд сходится. Сравним его с исходным рядом
, то подобранный ряд сходится. Сравним его с исходным рядом
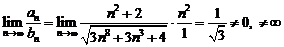 .
.
Значит, исходный ряд также сходится.
е) Это числовой знакочередующийся ряд. Проверим выполнение условий признака Лейбница 1) 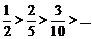 ; 2)
; 2) 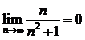 . Они выполняются. Исследуем сходимость соответствующего знакоположительного ряда
. Они выполняются. Исследуем сходимость соответствующего знакоположительного ряда 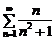 . Подберем обобщенный гармонический ряд
. Подберем обобщенный гармонический ряд  . Этот ряд расходящийся. По предельному признаку сравнения
. Этот ряд расходящийся. По предельному признаку сравнения  . Значит ряд
. Значит ряд 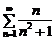 также расходится. Таким образом, ряд
также расходится. Таким образом, ряд  сходится условно.
сходится условно.
Задача 6. Разложить в ряды Фурье следующие функции:
а)  на интервале
на интервале 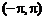 ;
;
б) 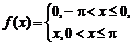 на интервале
на интервале 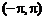 .
.
Решение. а) Определим коэффициенты Фурье:
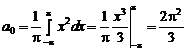 ;
;

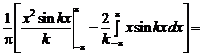
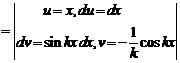
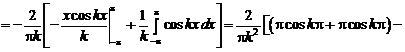
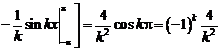 ;
;
 , так как функция четная.
, так как функция четная.
Итак, 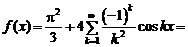
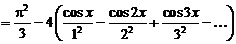 .
.
Если продолжить эту функцию на всю числовую ось, исходя из свойства периодичности, то получим непрерывную функцию, для которой это равенство выполняется для всех  .
.
Ответ: 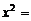
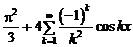 ,
, 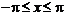 .
.
б) Определим коэффициенты Фурье:
 ;
;
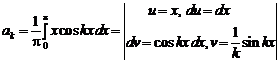
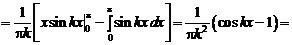
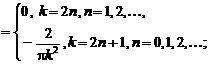

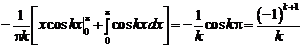 .
.
Таким образом, 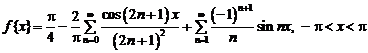 .
.
Заметим, что если продолжить эту функцию на всю числовую ось, исходя из свойства периодичности, то получим разрывную функцию. В точках разрыва  ,
, 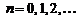 сумма ряда равна среднему арифметическому пределов полученной функции слева и справа, т.е. числу
сумма ряда равна среднему арифметическому пределов полученной функции слева и справа, т.е. числу  .
.
Ответ:  .
.