ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение
Высшего профессионального образования
«Тверской государственный технический университет»
Кафедра (предметная комиссия) ИНФОРМАЦИОННЫЕ СИСТЕМЫ
СОГЛАСОВАНО УТВЕРЖДАЮ
Гл. специалист предприятия, Заведующий кафедрой ИС
для которого выполнен
реальный проект (работа)
подпись, инициалы, фамилия подпись, инициалы, фамилия
““ 2011г. ““ 2011г.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
К курсовому проекту (работе)
На тему: « Сеть GRNN и аппроксимация функций (demogrn1)»
Автор курсового проекта (работы) Фролова А.Ю.
подпись, инициалы, фамилия
Обозначение курсового проекта (работы) группа ПИЭ-0908
Специальность прикладная информатика в экономике ПИЭ 0908 _______________________
номер, наименование
Руководитель проекта (работы)
подпись, дата инициалы, фамилия
Проект (работа) защищен(а) _______________________ оценка______________________________
дата
Консультанты по разделам:
Аналитическая часть ________
краткое наименование раздела подпись, дата, инициалы, фамилия
Проектная часть _____________
краткое наименование раздела подпись, дата, инициалы, фамилия
Нормоконтролер ___________________________________
подпись, дата, инициалы, фамилия
Тверь 2011
город год защиты
Тверской государственный технический университет
Кафедра Информационные системы
УТВЕРЖДАЮ
Заведующий кафедрой ИС
(подпись)
" "2011 г.
ЗАДАНИЕ
на выполнение курсового проекта (работы)
Студенту Фроловой А.Ю.,
1. Тема проекта (работы): « Сеть GRNN и аппроксимация функций (demogrn1) »
(утверждена приказом по ВУЗу от№ _______).
2. Срок сдачи студентом законченного проекта (работы)
3. Исходные данные к проекту (работе)
4. Содержание расчётно-пояснительной записки курсового проекта (работы):
а) Аналитическая часть
б) Проектная часть
5. Перечень графического (иллюстративного) материала:
6. Консультанты по проекту (работе) с указанием относящихся к ним разделов проекта
7. Дата выдачи задания
Руководитель
подпись
Задание принял к исполнению “”2011г.
(подпись студента)
| ||||||||||
| Изм. | Лист | № документа | Подпись | Дата | ||||||
| Разработала | Фролова А.Ю. |
| Литера | Лист | Листов | |||||
| Проверила | . | У | ||||||||
| Консультант | . | ТГТУ,0908 | ||||||||
| Утвердил | ||||||||||
Содержание
Введение………………………………………………………………………………….…...4
1. Теоретическая часть ……………………………...………………………………......5
1.1 Краткий исторический обзор............................…..……...................................................5
1.2 Биологические нейронные сети……….………..……………..........................................6
1.3 Модель технического нейрона……………………………...…………….………………8
1.4 Архитектура нейронной сети…………………………………………………………......9
1.5 Обучение нейронной сети………………………………………………………………...10
2. Многослойные сети прямого распространения…..………..……....................14
2.1 Многослойный персептрон………..……………………………………….…………....17
2.2 Сеть обобщённой нейронной регрессии (GRNN)..……...…………………………….. 20
2.3 Краткое описание возможностей ПС MATLAB 6.1 и тулбокса NNT……………....22
3. Проектная часть………………………………………………………….......................24
Применение сети обобщённой регрессии (GRNN) для решения задачи
аппроксимации функции.……………………………….………………………………..….21
3.2 Руководство пользователя….................................................…………………….……...29
4. Заключение……………………………………………………………..…………………31
5. Список литературы………………………………………………………......................33
| ||||||||||
| Изм. | Лист | № документа | Подпись | Дата | ||||||
| Разработала | Фролова А.Ю. |
| Литера | Лист | Листов | |||||
| Проверила | У | |||||||||
| Консультант | ТГТУ,0908 | |||||||||
| Утвердил | ||||||||||
| Введение В последние десятилетия в мире бурно развивается новая прикладная область математики, специализирующаяся на искусственных нейронных сетях (ИНС). Актуальность исследований в этом направлении подтверждается массой различных применений ИНС. Это автоматизация процессов распознавания образов, адаптивное управление, аппроксимация функционалов, прогнозирование, создание экспертных систем, организация ассоциативной памяти и многие другие приложения. С помощью искусственных нейронных сетей можно, например, предсказывать показатели биржевого рынка, выполнять распознавание оптических или звуковых сигналов, создавать самообучающиеся системы, способные синтезировать речь по тексту. Искусственная нейронная сеть (ИНС) - это набор нейронов, соединенных между собой. Как правило, передаточные функции всех нейронов в нейронной сети фиксированы, а веса являются параметрами нейронной сети и могут изменяться. Некоторые входы нейронов помечены как внешние входы нейронной сети, а некоторые выходы - как внешние выходы нейронной сети. Подавая любые числа на входы нейронной сети, мы получаем какой-то набор чисел на выходах нейронной сети. Таким образом, работа нейронной сети состоит в преобразовании входного вектора в выходной вектор, причем это преобразование задается весами нейронной сети. Практически любую задачу можно свести к задаче, решаемой нейронной сетью. |
Данный курсовой проект состоит из двух частей: аналитической части и проектной части. В аналитической части приводятся основные понятия нейронных сетей, методы применения нейронных сетей при решении задач. В проектной части разрабатывается приложение в среде ПС MATLAB 6 Notebook для решения задачи из состава демонстрационных примеров тулбокса NNT, реализованной в виде М-файла MATLAB: сеть GRNN и аппроксимация функций (demogrn1).
| ||||||||||
| Изм. | Лист | № документа | Подпись | Дата | ||||||
| Разработала | Фролова А.Ю. |
| Литера | Лист | Листов | |||||
| Проверила | У | |||||||||
| Консультант | ТГТУ,0908 | |||||||||
| Утвердил | ||||||||||
1.Теоретическая часть
1.1 Краткий исторический обзор
Искусственные нейронные сети (ИНС) — математические модели, а также их программные или аппаратные реализации, построенные по принципу организации и функционирования биологических нейронных сетей — сетей нервных клеток живого организма. Это понятие возникло при изучении процессов, протекающих в мозге, и при попытке смоделировать эти процессы. Исследования в области искусственных нейронных сетей (ИНС) пережили три периода активизации. Первый пик в 40-х годах обусловлен работой МакКаллока и Питтса. Второй возник в 60-х благодаря теореме сходимости перцептрона Розенблатта и работе Минского и Пейперта, указавшей ограниченные возможности простейшего перцептрона. Результаты Минского и Пейперта погасили энтузиазм большинства исследователей, особенно тех, кто работал в области вычислительных наук. Возникшее в исследованиях по нейронным сетям затишье продлилось почти 20 лет. С начала 80-х годов ИНС вновь привлекли интерес исследователей, что связано с энергетическим подходом Хопфилда и алгоритмом обратного распространения для обучения многослойного перцептрона (многослойные сети прямого распространения), впервые предложенного Вербосом и независимо разработанного рядом других авторов. Алгоритм получил известность благодаря Румельхарту, в 1986году Андерсон и Розенфельд подготовили подробную историческую справку о развитии ИНС.
1.2 Биологические нейронные сети
Нейрон (нервная клетка) является особой биологической клеткой, которая обрабатывает информацию (рис. 1). Она состоит из тела клетки (cell body), или сомы (soma), и двух типов внешних древоподобных ветвей: аксона (axon) и дендритов (dendrites). Тело клетки включает ядро (nucleus), которое содержит информацию о наследственных свойствах, и плазму, обладающую молекулярными средствами для производства необходимых нейрону материалов. Нейрон получает сигналы (импульсы) от других нейронов через дендриты (приемники) и передает сигналы, сгенерированные телом клетки, вдоль аксона (передатчик), который в конце разветвляется на волокна (strands). На окончаниях этих волокон находятся синапсы (synapses).
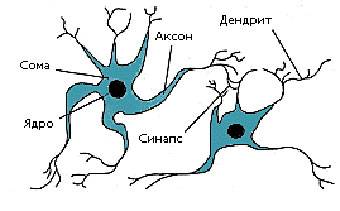
Рисунок 1. Схема биологического нейрона
Синапс является элементарной структурой и функциональным узлом между двумя нейронами (волокно аксона одного нейрона и дендрит другого). Когда импульс достигает синаптического окончания, высвобождаются определенные химические вещества, называемые нейротрансмиттерами. Нейротрансмиттеры диффундируют через синаптическую щель, возбуждая или затормаживая, в зависимости от типа синапса, способность нейрона-приемника генерировать электрические импульсы. Результативность синапса может настраиваться проходящими через него сигналами, так что синапсы могут обучаться в зависимости от активности процессов, в которых они участвуют. Эта зависимость от предыстории действует как память, которая, возможно, ответственна за память человека.
Кора головного мозга человека является протяженной, образованной нейронами поверхностью толщиной от 2 до 3 мм с площадью около 2200 см2 и содержит около 1011 нейронов. Каждый нейрон связан с 103 - 104 другими нейронами. В целом мозг человека содержит приблизительно от 1014 до 1015 взаимосвязей.
Нейроны взаимодействуют посредством короткой серии импульсов, как правило, продолжительностью несколько мсек. Сообщение передается посредством частотно-импульсной модуляции. Частота может изменяться от нескольких единиц до сотен герц, что в миллион раз медленнее, чем самые быстродействующие переключательные электронные схемы. Тем не менее, сложные решения по восприятию информации, как, например, распознавание лица, человек принимает за несколько сотен мсек. Эти решения контролируются сетью нейронов, которые имеют скорость выполнения операций всего несколько мсек. Это означает, что вычисления требуют не более 100 последовательных стадий. Другими словами, для таких сложных задач мозг "запускает" параллельные программы, содержащие около 100 шагов. Рассуждая аналогичным образом, можно обнаружить, что количество информации, посылаемое от одного нейрона другому, должно быть очень маленьким (несколько бит). Отсюда следует, что основная информация не передается непосредственно, а захватывается и распределяется в связях между нейронами. Этим объясняется такое название, как коннекционистская модель, применяемое к ИНС.
1.3 Модель технического нейрона
МакКаллок и Питтс предложили использовать бинарный пороговый элемент в качестве модели искусственного нейрона. Этот математический нейрон вычисляет взвешенную сумму n входных сигналов xj, j = 1, 2... n, и формирует на выходе сигнал величины 1, если эта сумма превышает определенный порог u, и 0 - в противном случае.
Часто удобно рассматривать u как весовой коэффициент, связанный с постоянным входом x0 = 1. Положительные веса соответствуют возбуждающим связям, а отрицательные - тормозным. МакКаллок и Питтс доказали, что при соответствующим образом подобранных весах совокупность параллельно функционирующих нейронов подобного типа способна выполнять универсальные вычисления. Здесь наблюдается определенная аналогия с биологическим нейроном: передачу сигнала и взаимосвязи имитируют аксоны и дендриты, веса связей соответствуют синапсам, а пороговая функция отражает активность сомы.
1.4 Архитектура нейронной сети
ИНС может рассматриваться как направленный граф со взвешенными связями, в котором искусственные нейроны являются узлами. По архитектуре связей ИНС могут быть сгруппированы в два класса (рис. 2): сети прямого распространения, в которых графы не имеют петель, и рекуррентные сети, или сети с обратными связями.

Рисунок 2. Систематизация архитектур сетей прямого распространения
В наиболее распространенном семействе сетей первого класса, называемых многослойным персептроном, нейроны расположены слоями и имеют однонаправленные связи между слоями. На рис. 2 представлены типовые сети каждого класса. Сети прямого распространения являются статическими в том смысле, что на заданный вход они вырабатывают одну совокупность выходных значений, не зависящих от предыдущего состояния сети. Рекуррентные сети являются динамическими, так как в силу обратных связей в них модифицируются входы нейронов, что приводит к изменению состояния сети.
1.5 Обучение
Способность к обучению является фундаментальным свойством мозга. В контексте ИНС процесс обучения может рассматриваться как настройка архитектуры сети и весов связей для эффективного выполнения специальной задачи. Обычно нейронная сеть должна настроить веса связей по имеющейся обучающей выборке. Функционирование сети улучшается по мере итеративной настройки весовых коэффициентов. Свойство сети обучаться на примерах делает их более привлекательными по сравнению с системами, которые следуют определенной системе правил функционирования, сформулированной экспертами.
Для конструирования процесса обучения, прежде всего, необходимо иметь модель внешней среды, в которой функционирует нейронная сеть - знать доступную для сети информацию. Во-вторых, необходимо понять, как модифицировать весовые параметры сети, какие правила обучения управляют процессом настройки. Алгоритм обучения означает процедуру, в которой используются правила обучения для настройки весов.
Существуют три парадигмы обучения: "с учителем", "без учителя" (самообучение) и смешанная. В первом случае нейронная сеть располагает правильными ответами (выходами сети) на каждый входной пример. Веса настраиваются так, чтобы сеть производила ответы как можно более близкие к известным правильным ответам. Усиленный вариант обучения с учителем предполагает, что известна только критическая оценка правильности выхода нейронной сети, но не сами правильные значения выхода. Обучение без учителя не требует знания правильных ответов на каждый пример обучающей выборки. В этом случае раскрывается внутренняя структура данных или корреляции между образцами в системе данных, что позволяет распределить образцы по категориям. При смешанном обучении часть весов определяется посредством обучения с учителем, в то время как остальная получается с помощью самообучения.
Теория обучения рассматривает три фундаментальных свойства, связанных с обучением по примерам: емкость, сложность образцов и вычислительная сложность. Под емкостью понимается, сколько образцов может запомнить сеть, и какие функции и границы принятия решений могут быть на ней сформированы. Сложность образцов определяет число обучающих примеров, необходимых для достижения способности сети к обобщению. Слишком малое число примеров может вызвать "переобученность" сети, когда она хорошо функционирует на примерах обучающей выборки, но плохо - на тестовых примерах, подчиненных тому же статистическому распределению.
Известны 4 основных типа правил обучения:
· коррекция по ошибке;
· машина Больцмана;
· правило Хебба;
· обучение методом соревнования.
Правило коррекции по ошибке. При обучении с учителем для каждого входного примера задан желаемый выход d. Реальный выход сети y может не совпадать с желаемым. Принцип коррекции по ошибке при обучении состоит в использовании сигнала (d-y) для модификации весов, обеспечивающей постепенное уменьшение ошибки. Обучение имеет место только в случае, когда перцептрон ошибается. Известны различные модификации этого алгоритма обучения.
Обучение Больцмана. Представляет собой стохастическое правило обучения, которое следует из информационных теоретических и термодинамических принципов. Целью обучения Больцмана является такая настройка весовых коэффициентов, при которой состояния видимых нейронов удовлетворяют желаемому распределению вероятностей. Обучение Больцмана может рассматриваться как специальный случай коррекции по ошибке, в котором под ошибкой понимается расхождение корреляций состояний в двух режимах.
Правило Хебба. Самым старым обучающим правилом является постулат обучения Хебба. Хебб опирался на следующие нейрофизиологические наблюдения: если нейроны с обеих сторон синапса активизируются одновременно и регулярно, то сила синаптической связи возрастает. Важной особенностью этого правила является то, что изменение синаптического веса зависит только от активности нейронов, которые связаны данным синапсом. Это существенно упрощает цепи обучения в реализации VLSI.
Обучение методом соревнования. В отличие от обучения Хебба, в котором множество выходных нейронов могут возбуждаться одновременно, при соревновательном обучении выходные нейроны соревнуются между собой за активизацию. Подобное обучение имеет место в биологических нейронных сетях. Обучение посредством соревнования позволяет кластеризовать входные данные: подобные примеры группируются сетью в соответствии с корреляциями и представляются одним элементом.
При обучении модифицируются только веса "победившего" нейрона. Эффект этого правила достигается за счет такого изменения сохраненного в сети образца (вектора весов связей победившего нейрона), при котором он становится чуть ближе к входному примеру. На рис.3 дана геометрическая иллюстрация обучения методом соревнования. Входные векторы нормализованы и представлены точками на поверхности сферы. Векторы весов для трех нейронов инициализированы случайными значениями. Их начальные и конечные значения после обучения отмечены Х на рис. 3а и 3б соответственно. Каждая из трех групп примеров обнаружена одним из выходных нейронов, чей весовой вектор настроился на центр тяжести обнаруженной группы.
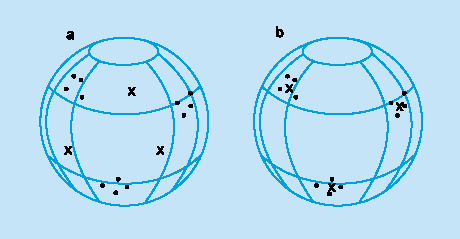
Рисунок 3.Пример обучения методом соревнования: (а) перед обучением; (б) после
Можно заметить, что сеть никогда не перестанет обучаться, если параметр скорости обучения не равен 0. Некоторый входной образец может активизировать другой выходной нейрон на последующих итерациях в процессе обучения. Это ставит вопрос об устойчивости обучающей системы. Система считается устойчивой, если ни один из примеров обучающей выборки не изменяет своей принадлежности к категории после конечного числа итераций обучающего процесса. Один из способов достижения стабильности состоит в постепенном уменьшении до 0 параметра скорости обучения. Однако это искусственное торможение обучения вызывает другую проблему, называемую пластичностью и связанную со способностью к адаптации к новым данным. Эти особенности обучения методом соревнования известны под названием дилеммы стабильности-пластичности Гроссберга.
В Таблице 2 представлены различные алгоритмы обучения и связанные с ними архитектуры сетей. В последней колонке перечислены задачи, для которых может быть применен каждый алгоритм. Каждый алгоритм обучения ориентирован на сеть определенной архитектуры и предназначен для ограниченного класса задач.
Таблица2
Известные алгоритмы обучения.
