Параметрическое уравнение прямой в пространстве
Параметрические уравнения прямой могут быть записаны следующим образом
| x = l t + x0 |
| y = m t + y0 | |
| z = n t + z0 |
где (x0, y0, z0) - координаты точки лежащей на прямой, {l; m; n}- координаты направляющего вектора прямой.
Каноническое уравнение прямой в пространстве
Если известны координаты точки A(x0, y0, z0) лежащей на прямой и направляющего вектора n = {l;m; n}, то уравнение прямой можно записать в каноническом виде, используя следующую формулу
| x- x0 | = | y- y0 | = | z- z0 |
| l | m | n |
Прямая как линия пересечения двух плоскостей
Если прямая является пересечением двух плоскостей, то ее уравнение можно задать следующей системой уравнений
|
| A1x+ B1y+ C1z + D1 = 0 |
| A2x+ B2y+ C2z + D2 = 0 |
при условии, что не имеет место равенство
| A1 | = | B1 | = | C1 | . |
| A2 | B2 | C2 | |||
Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю.
= 
— транспонированная матрица алгебраических дополнений;
Св-ва обратной матрицы:
· (A-1)-1 = A
· 
для любых двух обратимых матриц А и В.
· 
где Т обозначает транспонированную матрицу.
· 
для любого коэффициента k≠0.
Рангом системы строк (столбцов) матрицы A с m строк и n столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы. Обычно ранг матрицы A обозначается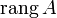 
(
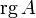) или 
.
Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.
Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.
Элементарные преобразования используются в методе Гаусса для приведения матрицы к треугольному или ступенчатому виду
Элементарными преобразованиями строк называют:
· перестановка местами любых двух строк матрицы;
· умножение любой строки матрицы на константу k, k≠0
· прибавление к любой строке матрицы другой строки.
Аналогично определяются элементарные преобразования столбцов. Элементарные преобразования обратимы. Обозначение 
указывает на то, что матрица A может быть получена из B путём элементарных преобразований (или наоборот).
векторов линейного пространства L линейно выражается через остальные векторы системы, то система векторов называется линейно зависимой.
Система векторов, которая не является линейно зависимой, называется линейно независимой.
Размерностью векторного пространства называется число, равное максимальному количеству линейно независимых векторов в этом пространстве.
Базис векторного пространства – это упорядоченная совокупность линейно независимых векторов этого пространства, число которых равно размерности пространства.
Примеры
· Нулевое пространство, единственным элементом которого является ноль.
· Любое поле является одномерным пространством над собой.
· 
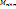- матрица n×m с элементами из R
· 
– множество свободных векторов(пространств, плоскостей)
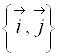описывается уравнением 
. Ее первые три слагаемые образуют квадратичную форму 
с матрицей:
.
Задача о приведении кривой 
этой кривой.
Пусть 
и 
– собственные значения матрицы A, а 
и 
– ортонормированные собственные векторы матрицы A, соответствующие собственным значениям 
и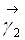 
называются главными направлениями этой кривой.
Пусть 
является матрицей перехода от ортонормированного базиса 
.
Тогда ортогональное преобразование:
Приводит квадратичную форму 
, а уравнение кривой – к виду 
в прямоугольной декартовой системе координат 
, оси которой направлены вдоль векторов 
, а начало совпадает с точкой O системы координат XY.
Выделив в этом уравнении полные квадраты, получим 
, где 
– некоторые числа. Осуществив параллельный перенос системы координат 
, получим канонический вид уравнения 
в системе координат 
. В зависимости от чисел 
эта кривая будет эллипсом, гиперболой, параболой, парой прямых, точкой или мнимой кривой.