Собственные числа и собственные векторы линейного оператора.
Определение 1. Пусть X – линейное пространство над K,  . Будем говорить, что
. Будем говорить, что  является собственным числом линейного оператора A, если существует такой ненулевой вектор
является собственным числом линейного оператора A, если существует такой ненулевой вектор  , что
, что  .
.
При этом вектор  называют собственным вектором оператора A, соответствующим собственному числу l.
называют собственным вектором оператора A, соответствующим собственному числу l.
Пример 1. Собственным числом тождественного оператора является 1, так как  для любого вектора
для любого вектора  .
.
Любой ненулевой вектор  – собственный вектор оператора E, соответствующий собственному числу
– собственный вектор оператора E, соответствующий собственному числу  .
.
Лемма. Ненулевая линейная комбинация собственных векторов, соответствующих одному и тому же собственному числу l линейного оператора A, также является собственным вектором, отвечающим l.
Доказательство. Пусть  - собственные векторы оператора A, соответствующие собственному числу
- собственные векторы оператора A, соответствующие собственному числу  , т.е.
, т.е.  для всех
для всех  . Пусть, далее,
. Пусть, далее,  - ненулевая линейная комбинация этих векторов. Покажем, что вектор
- ненулевая линейная комбинация этих векторов. Покажем, что вектор  также является собственным вектором, отвечающим l.
также является собственным вектором, отвечающим l.
Действительно,  .
.
Теорема 1. Критерий собственных чисел.
Пусть X – линейное пространство над K,  . Для того чтобы
. Для того чтобы  было собственным числом оператора A, необходимо и достаточно, чтобы это число было корнем характеристического многочлена
было собственным числом оператора A, необходимо и достаточно, чтобы это число было корнем характеристического многочлена  оператора A, т.е.
оператора A, т.е.  ,
,
или кратко: l – собственное число оператора  Û
Û  .
.
Доказательство. Введём обозначения:  - базис пространства X,
- базис пространства X,  X. По определению 1 утверждение “l – собственное число оператора A ” означает, что существует ненулевой вектор
X. По определению 1 утверждение “l – собственное число оператора A ” означает, что существует ненулевой вектор  такой, что
такой, что  , или
, или 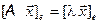 , где
, где  – базис
– базис 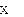 . По теореме 2 §3 последнее равенство эквивалентно следующему:
. По теореме 2 §3 последнее равенство эквивалентно следующему:  , или
, или  , где
, где  ,
,  , так как
, так как  . Это означает, что l – собственное число матрицы
. Это означает, что l – собственное число матрицы  , а по теореме 1 §5главы Y это возможно тогда и только тогда, когда
, а по теореме 1 §5главы Y это возможно тогда и только тогда, когда  , или
, или  .
.
Определение 2. Совокупность всех собственных чисел линейного оператора A (с учетом их кратностей как корней характеристического многочлена  ) будем называть спектром оператора A и обозначать так:
) будем называть спектром оператора A и обозначать так:  .
.
Пример 2. Пусть  . Найдем спектр тождественного оператора E.
. Найдем спектр тождественного оператора E.
Пусть  - базис X. Очевидно,
- базис X. Очевидно, 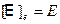 , и
, и
 .
.
Следовательно,  .
.
Пример 3. Пусть  – базис линейного пространства X над K,
– базис линейного пространства X над K,  , и
, и  . Найдем собственные числа и собственные векторы оператора
. Найдем собственные числа и собственные векторы оператора  .
.
По теореме 1, собственные числа оператора A есть корни характеристического многочлена  , где
, где  . В примере 1 §5главы Y были найдены корни этого многочлена
. В примере 1 §5главы Y были найдены корни этого многочлена  . Следовательно,
. Следовательно,  ,
,  – собственные числа линейного оператора
– собственные числа линейного оператора  , и
, и  . В этом же примере были найдены собственные векторы
. В этом же примере были найдены собственные векторы  и
и  матрицы
матрицы  , отвечающие собственным числам
, отвечающие собственным числам  и
и  соответственно:
соответственно:  ,
, 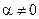 ;
;  , b и g не равны нулю одновременно. Следовательно, любой собственный вектор оператора A, соответствующий собственному числу
, b и g не равны нулю одновременно. Следовательно, любой собственный вектор оператора A, соответствующий собственному числу  имеет вид
имеет вид  , где
, где 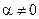 ; собственный вектор, соответствующий
; собственный вектор, соответствующий  , имеет вид
, имеет вид  , где b и g не равны нулю одновременно.
, где b и g не равны нулю одновременно.
Пример 4. Пусть X – линейное пространство над R,  ,
,  – базис X, и
– базис X, и  . Тогда оператор A не имеет ни собственных чисел, ни собственных векторов, так как его характеристический многочлен
. Тогда оператор A не имеет ни собственных чисел, ни собственных векторов, так как его характеристический многочлен  , не имеет вещественных корней.
, не имеет вещественных корней.
Теорема 2. Собственные векторы  линейного оператора
линейного оператора  , отвечающие попарно различным собственным числам
, отвечающие попарно различным собственным числам  , ¼,
, ¼,  соответственно (
соответственно ( , если
, если  ), линейно независимы.
), линейно независимы.
Доказательство проведем методом математической индукции по числу векторов  .
.
I. База. При  утверждение очевидно, так как собственный вектор ненулевой, а совокупность из одного ненулевого вектора линейно независима.
утверждение очевидно, так как собственный вектор ненулевой, а совокупность из одного ненулевого вектора линейно независима.
II. Индукционный переход. Докажем, что утверждение теоремы верно для  векторов, если оно верно для совокупностей из
векторов, если оно верно для совокупностей из  вектора.
вектора.
Пусть
 (1)
(1)
Подействуем на обе части этого равенства оператором A:
 , или
, или  .
.
Учитывая, что по условию  для
для  , получаем:
, получаем:
 . (2)
. (2)
Вычтем из равенства (2) равенство (1), умноженное на 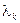 :
:
 .
.
Следовательно,  , так как совокупность
, так как совокупность  линейно независима по индукционному предположению. Отсюда получаем:
линейно независима по индукционному предположению. Отсюда получаем:  , так как
, так как  для
для  . Тогда из равенства (1) следует:
. Тогда из равенства (1) следует:  , откуда
, откуда  , так как
, так как  .
.
Итак, из равенства (1) следует:  , что и означает линейную независимость векторов
, что и означает линейную независимость векторов  .
.
Задача. Пусть  – линейно независимая совокупность собственных векторов линейного оператора
– линейно независимая совокупность собственных векторов линейного оператора  , соответствующих собственному числу
, соответствующих собственному числу  ,
,  , и пусть
, и пусть  , если
, если  . Докажите, что совокупность векторов
. Докажите, что совокупность векторов  линейно независима.
линейно независима.
§8. Операторы простой структуры.
Определение 1. Пусть  , l – собственное число оператора
, l – собственное число оператора  , т.е.
, т.е.  . Собственным подпространством линейного оператора
. Собственным подпространством линейного оператора  , соответствующим собственному числу l, будем называть ядро оператора
, соответствующим собственному числу l, будем называть ядро оператора  и обозначать его так:
и обозначать его так:  , т.е.
, т.е.
 .
.
Размерность собственного подпространства  будем называть геометрической кратностью собственного числа l и обозначать так:
будем называть геометрической кратностью собственного числа l и обозначать так:  .
.
Замечание 1. По лемме 1 §4 главы YIII 3, собственное подпространство, действительно, является подпространством пространства X как ядро линейного оператора  .
.
Замечание 2. Очевидно,  отличается от множества всех собственных векторов оператора A, соответствующих собственному числу l, лишь нулевым вектором, поскольку включение
отличается от множества всех собственных векторов оператора A, соответствующих собственному числу l, лишь нулевым вектором, поскольку включение  эквивалентно равенству
эквивалентно равенству  , или
, или  .
.
Задача. Докажите, что геометрическая кратность любого собственного числа l оператора  не превосходит его алгебраической кратности.
не превосходит его алгебраической кратности.
Определение 2. Будем говорить, что оператор  имеет простую структуру, если в пространстве
имеет простую структуру, если в пространстве 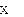 существует базис из собственных векторов оператора
существует базис из собственных векторов оператора  .
.