Пусть X – линейное пространство над K. Для того чтобы оператор 
имел простую структуру, необходимо и достаточно, чтобы было выполнено одно из следующих условий:
1. Матрица оператора A в произвольном базисе подобна диагональной.
2. Пространство X раскладывается в прямую сумму собственных подпространств оператора A, т.е. 
(здесь суммирование ведётся по всем различным точкам спектра).
3. Размерность пространства X равна сумме размерностей собственных подпространств оператора A, т.е. 
, или 
.
Доказательство. Необходимость первого критерия. Пусть A – оператор простой структуры, т.е.существует базис 
пространства X из собственных векторов этого оператора. Следовательно, 
для всех 
.Тогда [A ] 
([ A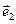 
] [A 
] 
[A 
] )=
([ 
] [ 
] [ 
] )= 
.
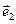Если 
- произвольный базис пространства X, то что [A ] 
= 
[A ] 
= 
[A ] , т.е.матрица что [A ] подобна матрице [A ] = 
.
Достаточность первого критерия. Пусть матрица [A ] подобна диагональной . По определению подобия это означает, что существует такая неособенная квадратная матрица 
, для которой справедливо равенство [A ] 
. Обозначим через такую совокупность векторов, что 
. Последнее равенство означает, что 
. По условию матрица неособенная. Следовательно, - базис пространства X и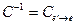 
Подсчитаем матрицу [A ] = [A ] 
= 
.
С другой стороны, [A ] ([ A 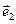] [A ] [A ] ).
Следовательно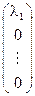, [A ] = 
= [ ] , , [A ] = 
= [ 
] , откуда получаем 
для всех . Таким образом, - базис пространства X из собственных векторов оператора 
. Следовательно, оператор имеет простую структуру.
Остальные критерии приводятся без доказательства.
Замечание. Первый критерий оператора простой структуры объясняет, почему вместо выражения “оператор имеет простую структуру” используют равносильное ему “оператор приводится к диагональному виду”.
|
|
Пример 1. Тождественный оператор 
имеет простую структуру, так как любой базис пространства 
состоит из его собственных векторов, поскольку 
для 
.
Пример 2. Покажем, что оператор из примера 3§7, матрица которого в базисе 
имеет вид 
, является оператором простой структуры.
В примере 3 были найдены спектр 
оператора и его собственные векторы. В частности, вектор 
– собственный вектор оператора , соответствующий собственному числу 
. Векторы 
и 
– собственные векторы оператора , соответствующие 
. Покажем, что совокупность векторов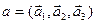 
линейно независимая. Подсчитаем ранг матрицы, составленной из координатных столбцов этих векторов в базисе 
: 
. Следовательно, совокупность векторов 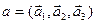линейно независимая, а т.к. 
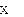=3, то это базис пространства, состоящий из собственных векторов оператора . Следовательно, – оператор простой структуры по определению 2.)
Пример 3. Пусть A – оператор дифференцирования из примера 5§1, т.е. 
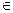L (X), где X= R 
и
A 
для любого 
X. В примере 1§ 6 был найден характеристический многочлен этого оператора 
. Следовательно, 
. В примере 1§4 было найдено ядро этого оператора 
A = 
. Следовательно, если A 
, то 
, и в пространстве X не существует базиса из собственных векторов оператора A. Таким образом, этот оператор не является оператором простой структуры.
Теорема 2. Если оператор , действующий в 
-мерном пространстве, имеет попарно различных собственных чисел, то этот оператор имеет простую структуру.
Доказательство. Пусть 
– собственные векторы оператора , отвечающие собственным числам 
, ¼, 
соответственно, причем 
, если 
.
|
|
По теореме 2 §7, совокупность 
линейно независимая и, следовательно,
является базисом пространства 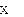из собственных векторов оператора , так как 
. Следовательно, по определению 2 оператор имеет простую структуру.
Пример 4. Покажем, что оператор , матрица которого в базисе имеет вид 
, имеет простую структуру.
Найдем характеристический многочлен оператора :
.
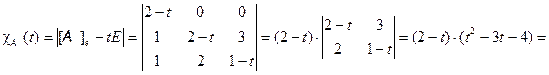
Следовательно, 
и по теореме 2 оператор имеет простую
структуру.