Частные производные функции нескольких переменных


26. Дифференцируемость функции
нескольких переменных. дифференциал
Дифференцируемые функции нескольких переменных.
Пусть функция двух переменных  определена в некоторой открытой области
определена в некоторой открытой области 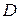 плоскости
плоскости  ,
,  – точка области
– точка области 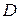 . Придавая переменным приращения
. Придавая переменным приращения 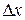 и
и  , перейдем из точки
, перейдем из точки  в какую-нибудь точку
в какую-нибудь точку 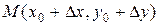 той же области. При этом функция
той же области. При этом функция  получит приращение
получит приращение
 .
.
В отличие от частных приращений  и
и  это приращение называется полным приращениемфункции
это приращение называется полным приращениемфункции  в точке
в точке  , соответствующим приращениям
, соответствующим приращениям 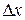 и
и  независимых переменных.
независимых переменных.
ОПРЕДЕЛЕНИЕ. Функция  называется дифференцируемой в точке
называется дифференцируемой в точке  если ее полное приращение в этой точке может быть записано в виде
если ее полное приращение в этой точке может быть записано в виде
 , (4.1)
, (4.1)
где 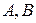 – некоторые числа,
– некоторые числа,  – бесконечно малые при
– бесконечно малые при  ,
,  (или, короче при
(или, короче при  ).
).
Замечание. Функции  и
и  зависят от
зависят от  .
.
Функция  , дифференцируемая в каждой точке некоторой области, называется дифференцируемой в этой области.
, дифференцируемая в каждой точке некоторой области, называется дифференцируемой в этой области.
Соотношение (4.1) можно записать и в более сжатой форме:
 (4.2)
(4.2)
где 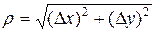 ,
,  – бесконечно малая при
– бесконечно малая при  .
.
Слагаемое  , линейное относительно
, линейное относительно 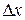 и
и  , является главной частью приращения, так как оставшееся слагаемое
, является главной частью приращения, так как оставшееся слагаемое  (или
(или 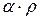 , если используется формула (4.2)) есть бесконечно малая более высокого порядка чем
, если используется формула (4.2)) есть бесконечно малая более высокого порядка чем 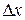 и
и  .
.
ПРИМЕР. Функция  будет дифференцируемой в любой точке
будет дифференцируемой в любой точке  , так как
, так как


Здесь  – главная часть полного приращения функции, а слагаемое
– главная часть полного приращения функции, а слагаемое 
 есть бесконечно малая более высокого порядка по сравнению с
есть бесконечно малая более высокого порядка по сравнению с 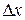 и
и  .
.
Данное выше определение дифференцируемости функции двух переменных является естественным обобщением определения дифференцируемости функции одной переменной. Следовательно, можно поставить вопрос о том, какие из свойств дифференцируемых функций одной переменной сохранятся для функции двух переменных. Так, было установлено, что если функция одной переменной дифференцируема в некоторой точке, то она непрерывна и имеет производную в этой точке. Последнее условие оказалось и достаточным, т.е. из существования производной функции одной переменной в данной точке следует дифференцируемость функции в этой точке. На функции двух переменных эти свойства переносится в следующем виде.
ТЕОРЕМА 4.1. (необходимые условия дифференцируемости). Если функция  дифференцируема в точке
дифференцируема в точке  , то она непрерывна в этой точке и имеет в ней частные производные по обеим независимым переменным. Причем
, то она непрерывна в этой точке и имеет в ней частные производные по обеим независимым переменным. Причем  , а
, а  .
.
ДОКАЗАТЕЛЬСТВО…
1) Пусть  дифференцируема в точке
дифференцируема в точке  . Значит ее приращение в этой точке может быть записано в виде
. Значит ее приращение в этой точке может быть записано в виде
 , (*)
, (*)
где 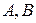 – некоторые числа,
– некоторые числа,  – бесконечно малые при
– бесконечно малые при  ,
,  . Тогда
. Тогда
 .
.
С другой стороны,
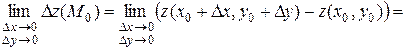
 .
.
Следовательно, 
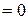 ,
,
⇒  ,
,
т.е.  непрерывна в точке
непрерывна в точке  .
.
2) Пусть  . Тогда формула (*) примет вид
. Тогда формула (*) примет вид
 ,
,
где  – некоторое число,
– некоторое число,  – бесконечно малая при
– бесконечно малая при  ,
,  . Отсюда получаем:
. Отсюда получаем: 
и  .
.
Аналогично доказывается, что существует 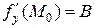 . ∎
. ∎
С учетом теоремы 4.1 равенства (4.1) и (4.2) можно теперь записать в виде  (4.3)
(4.3)
 (4.4)
(4.4)
где  – бесконечно малые при
– бесконечно малые при  ,
,  ,
,  ,
, 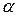 – бесконечно малая при
– бесконечно малая при  .
.
Утверждение обратное теореме 4.1 неверно. Из непрерывности функции двух переменных в точке и существования в этой точке ее частных производных еще не следует дифференцируемость функции.
ПРИМЕР. Функция  непрерывна в точке
непрерывна в точке  и имеет в этой точке частные производные:
и имеет в этой точке частные производные:
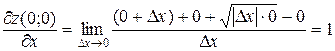 ,
,
 .
.
Однако эта функция не является дифференцируемой в точке  . Действительно, в этой точке ее полное приращение равно
. Действительно, в этой точке ее полное приращение равно
 .
.
Если бы функция была дифференцируемой в точке  , то слагаемое
, то слагаемое  можно было бы представить в виде
можно было бы представить в виде  , где
, где  , а
, а  – бесконечно малая при
– бесконечно малая при  . Но выделяя в
. Но выделяя в  множитель
множитель  , мы получаем второй множитель
, мы получаем второй множитель 
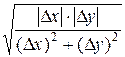 . А эта функция не является бесконечно малой при
. А эта функция не является бесконечно малой при  (при любых
(при любых  имеем
имеем 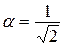 и, значит, в любой сколь угодно малой окрестности точки
и, значит, в любой сколь угодно малой окрестности точки  всегда найдутся точки
всегда найдутся точки  для которых неравенство
для которых неравенство  не выполняется для
не выполняется для  ).
).
Для того, чтобы функция двух переменных была дифференцируема в данной точке, на нее, в отличие от функции одной переменной надо наложить боле жесткие требования, чем существование частных производных в этой точке. А именно, справедлива следующая теорема.
ТЕОРЕМА 4.2. (достаточные условия дифференцируемости). Если функция  имеет в некоторой окрестности точки
имеет в некоторой окрестности точки 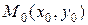 частные производные
частные производные  и
и  , причем в самой точке
, причем в самой точке 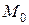 эти производные непрерывны, то функция
эти производные непрерывны, то функция  дифференцируема в этой точке.
дифференцируема в этой точке.
ПРИМЕР. 1) Функция  в любой точке
в любой точке  дифференцируема, так как ее частные производные
дифференцируема, так как ее частные производные  и
и  всюду непрерывны.
всюду непрерывны.
2) Функция  дифференцируема в каждой точке полуплоскости
дифференцируема в каждой точке полуплоскости  , так как там существуют и непрерывны ее частные производные
, так как там существуют и непрерывны ее частные производные  .
.
И в заключение этого пункта заметим, что все определения и теоремы, которые мы здесь формулировали, легко переносятся на случай функций большего числа переменных.
Дифференциал.
Пусть функция  дифференцируема в точке
дифференцируема в точке 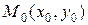 . Тогда, как было показано выше, ее полное приращение в этой точке может быть записано в виде
. Тогда, как было показано выше, ее полное приращение в этой точке может быть записано в виде
 ,
,
где 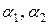 – бесконечно малые при
– бесконечно малые при  ,
,  .
.
ОПРЕДЕЛЕНИЕ. Пусть функция  дифференцируема в точке
дифференцируема в точке  . Главная, линейная относительно
. Главная, линейная относительно  и
и  часть ее полного приращения в этой точке, т.е.
часть ее полного приращения в этой точке, т.е.
 ,
,
называется полным дифференциалом функции  в этой точке и обозначается
в этой точке и обозначается  или
или  .
.
Из этого определения следует, что разность между полным приращением и полным дифференциалом функции в данной точке есть бесконечно малая более высокого порядка чем  и
и  :
:

где 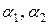 – бесконечно малые при
– бесконечно малые при  ,
,  . Это обстоятельство можно использовать в приближенных вычислениях.
. Это обстоятельство можно использовать в приближенных вычислениях.
Пусть, например, нам известны значения дифференцируемой функции  и ее частных производных
и ее частных производных  и
и  в точке
в точке  . Требуется вычислить значение этой функции в точке
. Требуется вычислить значение этой функции в точке  . Для этого рассмотрим разность значений функции в точке
. Для этого рассмотрим разность значений функции в точке  и
и 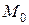 . По определению
. По определению
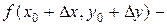

 .
.
Заменяя 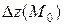 полным дифференциалом
полным дифференциалом  , получаем:
, получаем:


 ,
,
откуда


 . (4.5)
. (4.5)
Допущенная при этом погрешность будет тем меньше, чем меньше  и
и  .
.
ПРИМЕР. Вычислить приближенно 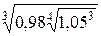 .
.
Рассмотрим функцию 
 . Искомое число представляет собой значение этой функции в точке
. Искомое число представляет собой значение этой функции в точке 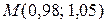 .
.
Пусть 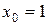 ,
,  . Так как частные производные рассматриваемой функции
. Так как частные производные рассматриваемой функции  ,
,  в точке
в точке  непрерывны, то функция дифференцируема в точке
непрерывны, то функция дифференцируема в точке 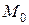 и для вычисления ее значения в точке
и для вычисления ее значения в точке  мы можем воспользоваться формулой (4.5).
мы можем воспользоваться формулой (4.5).
Имеем: 
 ,
,
 ,
,
 .
.
Из  ,
, 
находим, что  ,
,  .
.
Подставляя все в (4.5) окончательно получаем:


Данное выше определение полного дифференциала функции двух переменных легко обобщается на случай дифференцируемой функции любого числа переменных: полным дифференциалом функции 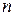 переменных в данной точке
переменных в данной точке  называется главная, линейная относительно приращений всех аргументов часть полного приращения функции в этой точке.
называется главная, линейная относительно приращений всех аргументов часть полного приращения функции в этой точке.
Полному дифференциалу функции двух переменных, как в свое время дифференциалу функции одной переменной, можно придать геометрический смысл. Но для этого нам придется ввести понятие касательной плоскости к поверхности. Сделать это можно несколькими, эквивалентными между собой, способами. Предлагаемое ниже определение является естественным обобщением определения касательной (прямой) к линии.
Пусть  – точка на поверхности
– точка на поверхности  . Возьмем на поверхности другую точку
. Возьмем на поверхности другую точку  и проведем секущую прямую
и проведем секущую прямую  .
.
 Плоскость, проходящая через точку Плоскость, проходящая через точку  , называется касательной плоскостью к поверхности в точке , называется касательной плоскостью к поверхности в точке  , если угол между секущей , если угол между секущей  и этой плоскостью стремится к нулю когда точка и этой плоскостью стремится к нулю когда точка  стремится к стремится к  , двигаясь по поверхности произвольным образом. , двигаясь по поверхности произвольным образом.
|


|
Из этого определения следует, что если у поверхности в данной точке есть касательная плоскость, то она единственная. Могут на поверхности быть и такие точки, в которых касательной плоскости к поверхности нет. Например, поверхность, заданная уравнением  (коническая поверхность) в точке
(коническая поверхность) в точке  касательной плоскости не имеет.
касательной плоскости не имеет.
Прямая, проходящая через точку  перпендикулярно касательной плоскости к поверхности в этой точке, называется нормалью к поверхности в точке
перпендикулярно касательной плоскости к поверхности в этой точке, называется нормалью к поверхности в точке  .
.
Позже мы покажем, что у поверхности, заданной уравнением  , где
, где  – функция, дифференцируемая в точке
– функция, дифференцируемая в точке 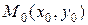 , касательная плоскость в точке
, касательная плоскость в точке  существует и имеет уравнение
существует и имеет уравнение 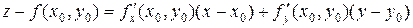 (4.6)
(4.6)
а нормаль в этой точке будет тогда иметь уравнение
 (4.7)
(4.7)
Если поверхность задана уравнением  , где
, где  – дифференцируемая в точке
– дифференцируемая в точке  функция, причем хотя бы одна из ее частных производных не обращается в этой точке в ноль, то касательная плоскость к поверхности в точке
функция, причем хотя бы одна из ее частных производных не обращается в этой точке в ноль, то касательная плоскость к поверхности в точке  существует и имеет уравнение
существует и имеет уравнение
 .
.
Уравнения нормали к поверхности в этой точки тогда будут иметь вид
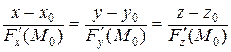 .
.
Замечание. Точка  поверхности
поверхности  , в которой все частные производные функции
, в которой все частные производные функции  обращаются в ноль, называется особой точкой поверхности. В особой точке поверхность может не иметь касательной плоскости.
обращаются в ноль, называется особой точкой поверхности. В особой точке поверхность может не иметь касательной плоскости.
 Выясним теперь геометрический смысл полного дифференциала функции двух переменных. Пусть функция
Выясним теперь геометрический смысл полного дифференциала функции двух переменных. Пусть функция  дифференцируема в точке
дифференцируема в точке 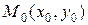 . Это значит, что поверхность, заданная уравнением
. Это значит, что поверхность, заданная уравнением  , имеет в точке
, имеет в точке 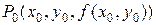 касательную плоскость, уравнение которой имеет вид (4.6). Полагая
касательную плоскость, уравнение которой имеет вид (4.6). Полагая  ,
,  , уравнение касательной плоскости можно переписать в виде
, уравнение касательной плоскости можно переписать в виде
 .
.
В этом равенстве слева стоит разность аппликат точек касательной плоскости, соответствующих точкам  и
и  , а справа – полный дифференциал функции
, а справа – полный дифференциал функции  в точке
в точке 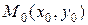 .
.
Таким образом, полный дифференциал функции  в точке
в точке 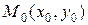 равен приращению, которое получает аппликата точки
равен приращению, которое получает аппликата точки  касательной плоскости, проведенной к графику функции
касательной плоскости, проведенной к графику функции  в точке
в точке 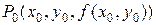 , когда ее координаты
, когда ее координаты  и
и 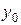 получают приращения
получают приращения  и
и  соответственно.
соответственно.
Полный дифференциал функции  в точке
в точке 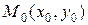 зависит от 1) координат точки, 2) от величины приращений
зависит от 1) координат точки, 2) от величины приращений  и
и  . Если рассматривать его во всех точках дифференцируемости функции и для всех возможный
. Если рассматривать его во всех точках дифференцируемости функции и для всех возможный  и
и 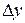 , то получим функцию четырех переменных (в общем случае
, то получим функцию четырех переменных (в общем случае  переменных), которую называют полным дифференциалом функции
переменных), которую называют полным дифференциалом функции 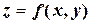 и обозначают
и обозначают  или
или  .
.
Легко доказать, что полный дифференциал функции нескольких переменных обладает теми же свойствами, что и дифференциал функции одной переменной. В том числе для него существует и вторая, инвариантная форма записи. Получим ее в заключение этого пункта.
Напомним, что если 
 – дифференцируемая функция двух независимых переменных, то по определению
– дифференцируемая функция двух независимых переменных, то по определению

 (4.8)
(4.8)
Полагая, в частности,  (т.е.
(т.е. 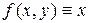 ), получаем
), получаем
 .
.
Аналогично, полагая  , получаем, что
, получаем, что  .
.
Поэтому мы можем записать дифференциал функции  в виде
в виде 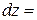
 . (4.9)
. (4.9)
Позже мы убедимся, что формула (4.9) остается верна и в том случае, когда  – сложная функция.
– сложная функция.
27. Дифференцирование сложной функции. Инвариантность формы первого дифференциала



ИНВАРИАНТНОСТЬ ФОРМЫПЕРВОГО ДИФФЕРЕНЦИАЛА
По определению дифференциал (первый дифференциал) функции 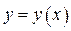 вычисляется по формуле
вычисляется по формуле  если
если 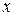 – независимая переменная.
– независимая переменная.
ПРИМЕР. 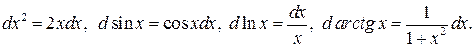
Покажем, что форма первого дифференциала остается неизменной (является инвариантной) и в том случае, когда аргумент функции 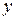 сам является функцией, то есть для сложной функции
сам является функцией, то есть для сложной функции  .
.
Пусть  дифференцируемы, тогда по определению
дифференцируемы, тогда по определению

Кроме того, 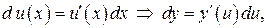 что и требовалось доказать.
что и требовалось доказать.
ПРИМЕРЫ.
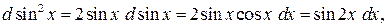

Доказанная инвариантность формы первого дифференциала позволяет считать, что 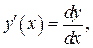 то есть производная равна отношению дифференциала функции к дифференциалу ее аргумента, независимо от того, является ли аргумент независимой переменной или функцией.
то есть производная равна отношению дифференциала функции к дифференциалу ее аргумента, независимо от того, является ли аргумент независимой переменной или функцией.