Практическая работа №11
Тема: « Решение тригонометрических уравнений »
Цели: отработать умения и навыки решения тригонометрических уравнений разными методами: разложение на множители; способ замены (сведение к алгебраическим уравнениям); сведение к уравнениям, однородным относительно 
и 
; преобразование суммы тригонометрических функций в произведение; преобразование произведения тригонометрических функций в сумму; использование формул понижения степени; равенство одноименных тригонометрических функций; введение вспомогательного аргумента.
Основные методы решения
Любое тригонометрическое уравнение в процессе решения с помощью надлежащих преобразований должно быть приведено к простейшим. Наиболее часто при решении тригонометрических уравнений применяются следующие методы:
- разложение на множители;
- способ замены (сведение к алгебраическим уравнениям);
- сведение к уравнениям, однородным относительно и ;
- преобразование суммы тригонометрических функций в произведение;
- преобразование произведения тригонометрических функций в сумму;
- использование формул понижения степени;
- введение вспомогательного аргумента.
При этом, как правило, в процессе решения тригонометрического уравнения приходится использовать не один, а несколько из указанных выше методов.
Способ замены
Данным методом решаются уравнения вида
.
Они сводятся к простейшим тригонометрическим уравнениям с помощью замены 
или 
. Уравнения 
не являются с виду алгебраическими, но их можно свести к алгебраическим:
.
Пример 1. Решить уравнение 
.
Решение. Это уравнение является квадратным относительно . Поэтому сделаем замену . В результате получим уравнение 
. Его корни: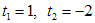 
, то есть получаем уравнение 
или 
. Первое уравнение дает 
. Второе уравнение не имеет корней.
Ответ: .
Пример 2. Решить уравнение 
.
Решение. Так как 
,
;
.
Сделаем замену 
.
, 
, 
.
; 
.
.
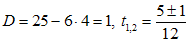Ответ: 
Однородные уравнения
,
,
называются однородными относительно и . Они обладают тем свойством, что сумма показаний степеней при и у всех членов уравнения одинакова. Делением на 
соответственно уравнения приводятся к алгебраическим уравнениям относительно 
. При этом, конечно, предполагается, что коэффициент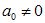 
. В результате получаем равносильное уравнение, так как разделили на 
(если бы 
, то из исходного уравнения следует, что и 
, а это невозможно, так как и при одном и том же значении х в нуль не обращаются, ибо всегда 
).
Пример 3. Решить уравнение:
.
Решение. Это уравнение является однородным относительно и . Поэтому, разделив его на 
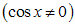, получим 
. Введем новую переменную 
и решим квадратное уравнение 
.
.
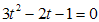или 
.
Ответ: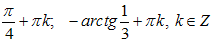 
.
Разложение на множители
При решении уравнений этим методом нужно пользоваться известными способами разложения на множители алгебраических выражений. Необходимо также знать уже приведенные формулы и дополнительно:
Пример 4. Решить уравнение 
.
Решение. Применяя формулу синуса двойного угла, получим 
, 
. Полученное уравнение равносильно совокупности уравнений: 
.
Решение 1-го уравнения: 
.
Уравнение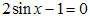 
преобразуем к виду , имеющему решение 
.
Ответ: 
.
Пример 5. Решить уравнение 
.
Решение. Перенесем все члены уравнения в левую часть и разложим ее на множители:
или 
,
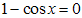или
или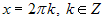 
.
Ответ: 
.
Преобразование суммы тригонометрических функций в произведение
Пример 6. Решить уравнение 
.
Решение. По формулам приведения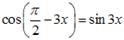 
. Получаем уравнение 
. Пользуясь, выше приведенной формулой, преобразуем разность синусов в произведение:
.
В результате имеем уравнение 
, откуда 
или 
. Решая эти уравнения, получим ;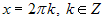 
.
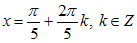Ответ: 
.