Лекция №1
Компьютерную графику можно классифицировать по нескольким основным признакам

Вторым классификационным признаком является способ формирования изображений, по которому компьютерная графика может быть разделена на растровую, векторную и фрактальную. Основным элементом растровой графики является точка, совокупность точек образует изображение. Векторная графика работает с линиями, которые описываются математически как единый объект. Фрактальная графика, как и векторная, основана на математических вычислениях, однако базовым элементом является сама математическая формула.
Растровая графика, основные понятия.
Все растровые изображения состоят из множества точек. Это наиболее простой способ представления изображения, потому, что именно таким образом видит его наш глаз.
Процесс формирования растрового изображения можно сравнить с мозаичным панно, где с помощью одинаковых по форме, но различных по цвету элементов создаются различные образы. Если отойти от мозаичного панно достаточно далеко, отдельные элементы становятся неразличимо малы, и изображение кажется однородным. Точно так же кодируются и растровые изображения в компьютерной графике. Все изображение подобно таблице разбивается по горизонтали и вертикали на мелкие ячейки – точки, каждая из которых принимает усредненный по площади ячейки цвет. При работе с изображением в памяти компьютера запоминается вся таблица (именно поэтому растровые изображения всегда прямоугольные) и цвет каждой ее точки. Таким образом, в растровых изображениях не существует объектов как таковых. Например, изображение древесного листа описывается конкретным расположением и цветом каждой точки сетки, поэтому при редактировании возникает необходимость работы с каждой конкретной точкой.
Пиксел - неделимая точка в графическом изображении. Пиксел характеризуется прямоугольной формой и размерами, определяющими пространственное разрешение изображения
Под растровым (bitmap, raster) понимают способ представления изображения в виде совокупности отдельных точек (пикселов) различных цветов или оттенков (Рис. 1.2). Это наиболее простой способ представления изображения, потому, что именно таким образом видит его глаз человека.
Растровый способ кодирования изображений обеспечивает легкость их ввода с помощью сканеров. Светочувствительный элемент сканера измеряет оптическую плотность сканируемого оригинала (рисунка, фотографии, слайда) по всей его площади: в отдельных точках с заданным интервалом вдоль и поперек оригинала. В результате получается прямоугольная таблица, каждая ячейка которой соответствует измеренному значению цвета. Она представляется точным снимком оригинала в цифровой форме. Каждая ячейка таблицы называется точкой, а вся таблица — растровым изображением.
Кроме того, есть мониторы, которые тоже является растровым устройством. Экран монитора покрыт прямоугольной сеткой из точек люминофора. При демонстрации изображения кодированная информация визуализируется с помощью операции, обратной сканированию. Каждой точке изображения ставится в соответствие точка люминофора, называемая пикселем. Пиксель принимает цвет соответствующей ему точке изображения. Поэтому точку цифрового изображения часто отождествляют с пикселем и говорят, что растровое изображение состоит из пикселей.
Монитор — не единственное устройство вывода. Изображение можно напечатать на принтере, типографской машине, вывести на фотопленку или фотобумагу. Большинство устройств вывода, как и мониторы, тоже являются растровыми устройствами, и точкам изображения ставятся в соответствие точки этих устройств.
Цифровое изображение, находящееся в памяти компьютера не имеет своего физического воплощения, это всего лишь набор цифр. Увидеть его можно только посредством какого-либо устройства вывода. По этой причине внешний вид изображения (размер, качество, цветопередача и т.п.) сильно зависят от характеристик монитора или принтера.
Достоинством растрового способа представления изображений является возможность получения фотореалистичного изображения высокого качества в различном цветовом диапазоне. Недостатком – высокая точность и широкий цветовой диапазон требуют увеличения объема файла для хранения изображения и оперативной памяти для его обработки.
Растровая графика описывает изображения с использованием цветных точек, называемых пикселами, расположенных на сетке. Например, изображение древесного листа описывается конкретным расположением и цветом каждой точки сетки, что создает изображение примерно так же, как в мозаике (фотографии, отсканированные рисунки и т.д.). При редактировании растровой графики редактируются пикселы, а не линии. Растровая графика зависит от разрешения, поскольку информация, описывающая изображение, прикреплена к сетке определенного размера. При редактировании растровой графики, качество ее представления может измениться. В частности, изменение размеров растровой графики может привести к «разлохмачиванию» краев изображения, поскольку пикселы будут перераспределяться на сетке. Вывод растровой графики на устройства с более низким разрешением, чем разрешение самого изображения, понизит его качество.
Применение растровой графики позволяет добиться качественного изображения, фотографического качества. Но за все нужно, платить в данном случае - объемами файлов и трудоемкостью редактирования изображения, приходиться каждую точку подправлять вручную. Даже если Вы при редактировании используете инструменты типа линии или примитивов (овалов, квадратов), то результат представляет собой изменение затронутых данными инструментами пикселей. При изменении размеров, качество изображения ухудшается: при уменьшении - исчезают мелкие детали, а при увеличении картинка может превратиться в набор неряшливых квадратов (увеличенных пикселей). При печати растрового изображения или при просмотре его на средствах имеющих недостаточный разрешающую способность значительно ухудшает восприятие образа.
Размер изображения
Растровые изображения характеризуются количеством составляющих их точек. В силу частого отождествления точек и пикселей размеры изображений измеряют в пикселях. Это представляется удобным, если изображение предназначено только для демонстрации на мониторе (Web-страницы и прочие документы для электронного распространения). Удобство обусловлено стандартизированным количеством пикселей, которое могут отображать мониторы. Для большинства мониторов эта величина составляет 800х600, 1024х768, 1152х864, 1280*960, 1280х1024, 1600х1200 и т.д.
Чтобы представить себе, сколько места на экране монитора займет изображение известного размера, надо знать, сколько пикселей монитора приходится на единицу длины. Такая величина имеет собственное название - разрешение экранного изображения, и измеряется в пикселях на дюйм (pixel per inch, ppi). В каждом конкретном случае она зависит от физического размера экрана и установленного размера растровой сетки, т. е. количества пикселей по вертикали и горизонтали. Число возможных сочетаний этих параметров весьма велико (например, разрешение мониторов могут быть установлены в диапазоне от 72 ppi до 96 ppi). При более высоком разрешении элементы интерфейса программ (текст в меню и диалоговых окнах, панели инструментов и т. п.) становятся слишком мелкими, глаза быстро утомляются. Низкое разрешение, наоборот, оставляет на экране слишком мало места для самого редактируемого изображения или текста.
Разрешение изображения – определяет насколько точно будут воспроизведены детали изображения. Чем выше разрешение, тем выше качество печати и тем больше объем данных изображения. Это, в свою очередь, означает необходимость большего объема памяти для записи изображения. Разрешение выражается в dpi (Dots Per Inch – Точках на дюйм). Например, разрешение 400 dpi означает, что в каждом дюйме присутствует 400 точек. Размер одной точки составляет примерно 63,5 микрон (0,0635 мм.).
Разрешение дисплея – это степень резкости изображения, показываемого на дисплее. Разрешение дисплея измеряется в dpi (точек/дюйм). Однако термин разрешение дисплея используется и для определения разрешающей способности самого дисплея. Разрешение дисплея заметно ниже разрешения принтера или сканера. Следовательно, если нужно создать изображение для основной страницы Web, то требования к разрешению будут намного ниже, чем возможности сканера или принтера (например, вполне достаточно будет разрешения 72 - 100 dpi).
Разрешение при печати – работа цветного струйного принтера основана на распылении чернильных частиц на бумажный или какой-либо другой носитель, используемый для печати. Разрешение при печати выражается числом чернильных частиц, которые можно распылить на один дюйм (примерно 2,54 мм.) бумаги. Например, разрешение 1440 dpi означает, что на длине одного дюйма бумаги будет распылено 1440 чернильных частиц. Чем больше число чернильных частиц, тем точнее воспроизводятся детали изображения. Однако при этом соответственно возрастает и время печати.
Выражать размер изображения в пикселях удобно при подготовке графики для электронного распространения. Если же цель состоит в получении печатной копии, то лучше оперировать метрическими единицами. Зная разрешение монитора, легко вычислить размер изображения на экране. Например, изображение размером 100х50 пикселей займет на экране примерно 1х0,5 дюйма == 25х13 мм (100 pix/96 ppi = 1,04 inch; 50 pix/96 ppi = 0,52 inch; 1 дюйм = 25,4 мм).
Приведенный расчет выполнен исходя из разрешения монитора 96 ppi. Для разрешения 72 ppi размер того же изображения окажется иным: 1,4х0,7 дюйма =35х18 мм (100 pix/72 ppi = 1,39 inch; 50 pix/72 ppi = 0,69 inch).
Производить подобные вычисления каждый раз, как только потребуется оценить размер изображения на конкретном устройстве вывода, не удобно. Поэтому размер растровых изображений чаще всего характеризуют так же, как и растровые устройства: разрешением. Вместо размера в пикселях при создании или сканировании изображения при этом указывают разрешение и геометрический размер в сантиметрах или дюймах. Цифровое изображение от этого не приобретает физических размеров. Такой способ эквивалентен предположению: «если бы изображение выводилось на устройстве с заданным разрешением, то оно имело бы заданный размер».
При создании или сканировании изображений всегда будут известны (хотя бы приблизительно) требуемый геометрический размер изображения и его разрешение. Геометрический размер определяется дизайном «бумажной» публикации или Web-страницы. Разрешение определяется предполагаемым устройством вывода. Задавая эти параметры еще при создании или сканировании изображений, пользователь не только избавляет себя от расчетов. Данные о геометрических размерах изображений используются при печати из специальных программ, работающих с компьютерной графикой и при размещении изображений в издательских системах и программах иллюстрирования. Соответствие при этом разрешения изображений разрешению устройства вывода будет на вашей совести.
В файлах изображений хранится информация о геометрическом размере и разрешении изображений. Эти величины используются при помещении изображения в программу верстки или подготовки иллюстраций.
При изменении размеров, качество растрового изображения ухудшается: при уменьшении - исчезают мелкие детали, а при увеличении картинка может превратиться в набор неряшливых квадратов (увеличенных пикселей). При печати растрового изображения или при просмотре его на средствах имеющих недостаточный разрешающую способность значительно ухудшает восприятие образа.
Векторная графика, основные понятия
Для векторной графики (object-oriented graphics) характерно разбиение изображения на ряд графических примитивов – точка, прямая, ломаная, дуга, полигон. Таким образом, появляется возможность хранить не все точки изображения, а координаты узлов примитивов и их свойства (цвет, связь с другими узлами и т.д.). При использовании векторного представления изображение представляет собой базу данных описаний примитивов. То есть, в составе изображения могут быть отрезки, окружности, овалы, точки, кривые Безье и так далее. А изображение будет представлять из себя массив описаний, например:
отрезок (20,20-100,80), окружность (50,40-30), кривая Безье (20,20-50,30-100,50)
Векторное изображение может быть легко масштабировано без потери деталей, т.к. это требует пересчета сравнительно небольшого числа координат узлов.
Векторная графика описывает изображения с использованием прямых и изогнутых линий, называемых векторами, а также параметров, описывающих цвета и расположение. Например, изображение древесного листа описывается точками, через которые проходит линия, создавая тем самым контур листа. Цвет листа задается цветом контура и области внутри этого контура.
Если в растровой графике базовым элементом изображения является точка, то в векторной графике — линия. Линия описывается математически как единый объект, и потому объем данных для отображения объекта средствами векторной графики существенно меньше, чем в растровой графике.
Линия — элементарный объект векторной графики. Как и любой объект, линия обладает свойствами: формой (прямая, кривая), толщиной, цветом, начертанием (сплошная, пунктирная). Окончание линии (то есть ее форма в конечном узле) также выступает одним из свойств с изменяемыми параметрами.
Замкнутые линии приобретают свойство заполнения. Охватываемое ими пространство может быть заполнено другими объектами (текстуры, карты) или выбранным цветом. Заполнение бывает растровым и векторным. В последнем случае иногда используют элементы фрактальной графики, являющейся частным случаем векторной. Основные языки программирования при выводе графических примитивов также используют понятия векторной графики.
Простейшая незамкнутая линия ограничена двумя точками, именуемыми узлами. Узлы имеют ряд свойств, параметры которых влияют на форму конца линии и характер сопряжения с другими объектами. Все прочие объекты векторной графики, в том числе самые сложные, составляют из линий (Рис. 1.4).

Рис. 1.4. Разомкнутый контур, замкнутый контур, комбинированный контур
Для построения объектов векторной графики используют инструменты рисования линий и управления заполнением контуров. Простые объекты могут взаимодействовать различными способами, в том числе с применением булевых операций объединения, вычитания и пересечения.
Эффекты, применимые к объектам векторной графики, воздействуют на свойства линии, заполнения и узлов. В программах векторной графики все эффекты являются модификаторами. Модификатор описывает математическими методами параметры изменения свойств исходного объекта, не затрагивая его основ. Именно на этом базируется возможность многоуровневого «отката», то есть возврата к исходному состоянию объекта.
Лекция №2
Математические основы векторной графики
Рассмотрим подробнее способы представления различных объектов в векторной графике.
Точка. Этот объект на плоскости представляется двумя числами (х, у), указывающими его положение относительно начала координат (Рис. 1.5).

Рис. 1.5. Точка на плоскости в системе координат
Прямая линия. Ей соответствует уравнение у = kx + b. Указав параметры к и b, всегда можно отобразить бесконечную прямую линию в известной системе координат, то есть для задания прямой достаточно двух параметров (Рис. 1.6).
Отрезок прямой. Он отличается тем, что требует для описания еще двух параметров — например, координат х1 и х2 начала и конца отрезка (Рис. 1.6). 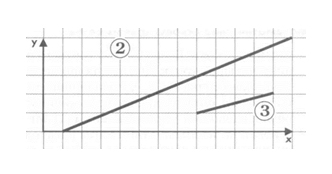
Рис. 1.6. Прямая линия и отрезок в системе координат
Кривая второго порядка. К этому классу кривых относятся параболы, гиперболы, эллипсы, окружности, то есть все линии, уравнения которых содержат степени не выше второй (Рис. 1.7). Кривая второго порядка не имеет точек перегиба. Прямые линии являются всего лишь частным случаем кривых второго порядка. Формула кривой второго порядка в общем виде может выглядеть, например, так:
х2 + а1у2 + а2ху + а3х + а4у + а5 = 0
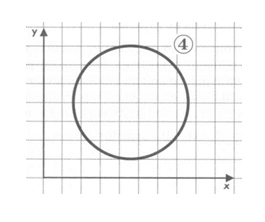
Рис. 1.7. Кривая второго порядка в системе координат
Для описания бесконечной кривой второго порядка достаточно пяти параметров. Если требуется построить отрезок кривой, понадобятся еще два параметра (Рис. 1.8).

Рис. 1.8. Бесконечная кривая второго порядка в системе координат
Кривая третьего порядка. Отличие этих кривых от кривых второго порядка состоит в возможном наличии точки перегиба. Например, график функции у = х3 имеет точку перегиба в начале координат. Именно эта особенность позволяет сделать кривые третьего порядка основой отображения природных объектов в векторной графике. Линии изгиба человеческого тела, контуры пересеченной местности, очертания растений весьма близки к кривым третьего порядка. Все кривые второго порядка, в том числе прямые линии, являются частными случаями кривых третьего порядка.
В общем случае уравнение кривой третьего порядка можно записать так:
х3 + а1у3 + а2х2у + а3ху2 + а4х2 + а5у2 + а6ху + а7х + а8у + а9 = 0
Таким образом, кривая третьего порядка описывается девятью параметрами (Рис. 1.9). Описание ее отрезка потребует на два параметра больше (Рис. 1.10). Несмотря на кажущуюся сложность описания кривой третьего порядка, ее код занимает в файле несравнимо меньше места, чем код аналогичной кривой, но созданной из точек (растровой). Для растровой линии дают описание положения и цвета каждой точки.

Рис. 1.9. Кривая третьего порядка в системе координат

Рис. 1.10. Описание отрезка кривой третьего порядка
Кривые Безье (Bezier). Кривые Безье были разработаны в 60-х годах XX века независимо друг от друга Пьером Безье (Bezier) из автомобилестроительной компании «Рено» и Полем де Кастелье (de Casteljau) из компании «Ситроен», где применялись для проектирования кузовов автомобилей.
Кривая Безье является гладкой кривой, то есть она не имеет разрывов и непрерывно заполняет отрезок между начальной и конечной точками.
Благодаря простоте задания и возможности удобно манипулировать формой, кривые Безье нашли широкое применение в компьютерной графике для моделирования гладких линий. Поскольку кривая полностью определяется своей выпуклой оболочкой из опорных точек, последние могут быть отображены и использоваться для наглядного управления формой линии. Кроме того, аффинные преобразования кривой (перенос, масштабирование, вращение) также легко могут быть осуществлены путём применения трансформаций к опорным точкам. Наличие выпуклой оболочки значительно облегчает задачу о точках пересечения кривых Безье: если не пересекаются выпуклые оболочки, то не пересекаются и сами кривые.
Наибольшее значение имеют кубические кривые Безье. Кривые высших степеней при обработке требуют большего объёма вычислений и для практических целей используются реже. Для построения сложных по форме линий отдельные кривые Безье могут быть последовательно соединены друг с другом в сплайн Безье. Для того, чтобы обеспечить гладкость линии в месте соединения двух кривых, смежные опорные точки обеих кривых должны лежать на одной линии.
Сегмент кривой Безье третьего порядка описывается положением четырех точек. Две из них являются опорными (узлами кривой): начальная точка Р0(х0,у0) и конечная точка Р3 (х3,у3). Точки Р1 (х1,у1) и Р2 (х2,у2), определяющие положение касательных относительно отрезка, называют управляющими (Рис. 1.11). Метод построения кривой Безье основан на использовании пары касательных (управляющих линий), проведенных к сегменту кривой в его окончаниях. На форму кривой влияют угол наклона касательной и длина ее отрезка.

Рис. 1.11. Сегмент кривой Безье третьего порядка
Параметрическое уравнение Безье описывает положение точек и, тем самым, форму кривой. Уравнение решают относительно параметра t, принимающего значения от 0 (в начальной точке) до 1 (в конечной точке). При построении сегмента кривой Безье на плоскости рассчитывают координаты х и у (для четырех точек, из них двух управляющих):

Следовательно:
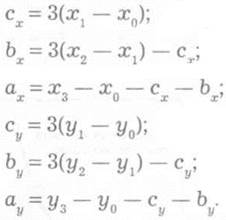
Значение t определяет степень влияния точек на форму кривой (Рис. 1.12 и Рис. 1.13). Например, при t = 0,333 наибольший «вес» приобретает точка Р1(х1, у1), а при t = 0,666 — точка Р2 (х2, у2). Из приведенных уравнений вытекает, что кривая может проходить лишь через начальную и конечную опорные точки сегмента (Р0, Р3). Тем самым достигаются простота описания и стабильность кривой Безье. 
Рис. 1.12. Степень влияния точек на форму кривой (1 вариант)

Рис. 1.13. Степень влияния точек на форму кривой (2 вариант)
Кривые Безье обладают рядом свойств, определяющих возможность их использования в векторной графике. С геометрической точки зрения, производной кривой Безье будет другая кривая Безье, векторы управляющих точек которой определяются вычислением разностей векторов управляющих точек исходной кривой.
Лекция №3
Основные свойства кривой Безье:
непрерывность заполнения сегмента между начальной и конечной точками
кривая всегда располагается внутри фигуры, образованной линиями, соединяющими контрольные точки (Рис. 1.14)

Рис. 1.14. Кривые, расположенные внутри фигуры
при наличии только двух контрольных точек сегмент представляет собой прямую линию (Рис. 1.15)

Рис. 1.15. Сегмент при наличии двух контрольных точек
прямая линия образуется при коллинеарном (на одной прямой) размещении управляющих точек (Рис. 1.16)

Рис. 1.16. Коллинеарное размещение точек
кривая Безье симметрична, то есть обмен местами между начальной и конечной точками (изменение направления траектории) не влияет на форму кривой (Рис. 1.17)

Рис. 1.17. Кривая Безье симметрична
масштабирование и изменение пропорций кривой Безье не нарушает ее стабильности, так как она с математической точки зрения «аффинно инвариантна» (Рис. 1.18, Рис. 1.19, Рис. 1.20 и Рис. 1.21)

Рис. 1.18. Исходная кривая

Рис. 1.19. Масштабирование и изменение пропорций кривой Безье

Рис. 1.20. Масштабирование и изменение пропорций кривой Безье (вращение)

Рис. 1.21. Масштабирование и изменение пропорций кривой Безье (перекос)
изменение координат хотя бы одной из точек ведет к изменению формы всей кривой Безье (Рис. 1.22)

Рис. 1.22. Изменение координат точек
степень кривой всегда на одну ступень ниже числа контрольных точек. То есть при трех контрольных точках форма кривой — парабола
размещение дополнительных контрольных точек вблизи одной позиции увеличивает ее «вес» и приводит к приближению траектории кривой к данной позиции (Рис. 1.23)

Рис. 1.23. Размещение дополнительных контрольных точек вблизи одной позиции
окружность не может быть описана параметрическим уравнением кривой Безье
невозможно создать параллельные кривые Безье, за исключением тривиальных случаев (прямые линии и совпадающие кривые)
При редактировании элементов векторной графики изменяют параметры прямых и изогнутых линий, описывающих форму этих элементов. Можно переносить элементы, менять их размер, форму и цвет, но это не отразится на качестве их визуального представления. Векторная графика не зависит от разрешения, т.е. может быть показана в разнообразных выходных устройствах с различным разрешением без потери качества.
Достоинством векторной компьютерной графики является:
Она экономна в плане объемов дискового пространства, необходимого для хранения изображений: это связано с тем, что сохраняется не само изображение, а только некоторые основные данные, используя которые программа всякий раз воссоздает изображение заново. Кроме того, описание цветовых характеристик несильно увеличивает размер файла
Объекты векторной графики просто трансформируются и ими легко манипулировать, что не оказывает практически никакого влияния на качество изображения
Векторная графика максимально использует возможности разрешающей способности любого выводного устройства: изображение всегда будет настолько качественным, насколько способно данное устройство
Недостатком векторной компьютерной графики является:
Программная зависимость: каждая программа сохраняет данные в своем собственном формате, поэтому изображение, созданное в одном векторном редакторе, как правило, не конвертируется в формат другой программы без погрешностей
Сложность векторного принципа описания изображения не позволяет автоматизировать ввод графической информации и сконструировать устройство подобное сканеру для растровой графики
Векторная графика действительно ограничена в чисто живописных средствах и не предназначена для создания фотореалистических изображений
Лекция №4
Фрактальная графика, основные понятия.
В математике существует понятие фрактала – геометрического образования, представляющего собой систему самоподобных фигур, расположенных относительно друг друга закономерным образом. Как форма и размер отдельных элементов, так и их взаимное расположение может быть описано математической формулой.
Фрактальная графика, как и векторная, основана на математических вычислениях. Базовым элементом фрактальной графики является сама математическая формула, т.е. никаких объектов в памяти компьютера не хранится и изображение строится исключительно по уравнениям. Таким образом, строят как простейшие регулярные структуры, так и сложные иллюстрации, имитирующие природные ландшафты и трехмерные объекты.
Фрактальная графика, как и векторная - вычисляемая, но отличается от неё тем, что никакие объекты в памяти компьютера не хранятся. Изображение строится по уравнению (или по системе уравнений), поэтому ничего, кроме формулы, хранить не надо. Изменив коэффициенты в уравнении, можно получить совершенно другую картину. Способность фрактальной графики моделировать образы живой природы вычислительным путем часто используют для автоматической генерации необычных иллюстраций.
Фрактал – это объект, обладающий бесконечной сложностью, позволяющий рассмотреть столько же своих деталей вблизи, как и издалека. Земля – классический пример фрактального объекта. Из космоса она выглядит как шаp. Если приближаться к ней, то будут видны океаны, континенты, побережья и цепи гор. Если рассматривать горы ближе – станут видны еще более мелкие детали: кусочек земли на поверхности горы в своем масштабе столь же сложный и неровный, как сама гора. И даже еще более сильное увеличение покажет крошечные частички грунта, каждая из которых сама является фрактальным объектом.
Многие объекты в природе обладают фрактальными свойствами, например побережья, облака, кроны деревьев, кровеносная система и система альвеол человека или животных.
Последнее время фракталы стали популярны у трейдеров для анализа курса фондовых бирж, валютных и торговых рынков.
Фракталы, особенно на плоскости, популярны благодаря сочетанию красоты с простотой построения при помощи компьютера (Рис. 1.24, Рис. 1.25, Рис. 1.26, Рис. 1.27, Рис. 1.28, Рис. 1.29, Рис. 1.30).
Фрактал (лат. fractus — дробленый) — термин, означающий геометрическую фигуру, обладающую свойством самоподобия, то есть составленную из нескольких частей, каждая из которых подобна всей фигуре целиком. В более широком смысле под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность, либо метрическую размерность, строго большую топологической.
Слово «фрактал» не является математическим термином и не имеет общепринятого строгого математического определения. Оно может употребляться, когда рассматриваемая фигура обладает какими-либо из перечисленных ниже свойств:
Обладает нетривиальной структурой на всех шкалах. В этом отличие от регулярных фигур (таких, как окружность, эллипс, график гладкой функции): если мы рассмотрим небольшой фрагмент регулярной фигуры в очень крупном масштабе, он будет похож на фрагмент прямой. Для фрактала увеличение масштаба не ведёт к упрощению структуры, на всех шкалах мы увидим одинаково сложную картину
Является самоподобной или приближённо самоподобной
Обладает дробной метрической размерностью или метрической размерностью, превосходящей топологическую
Может быть построена при помощи рекурсивной процедуры
Основоположником идей о фракталах считается Франко-Американский математик Профессор Бенуа Б. Мандельброт (Benoit B. Mandelbrot). В середине 1960х после десятилетий обучения и научной деятельности, Мандельброт разработал то, что он назвал фрактальная геометрия или геометрия природы (об этом он написал свою книгу — «Фрактальная геометрия природы»). Целью фрактальной геометрии был анализ сломанных, морщинистых и нечетких форм. Мандельброт использовал слово фрактал, потому, что это предполагало осколочность и фракционность этих форм.
Мандельброт и другие ученые, такие как Клиффорд А. Пикковер (Clifford A. Pickover), Джеймс Глейк (James Gleick) или Г. О. Пейтген (H.O. Peitgen) пытаются расширить область фрактальной геометрии так, чтобы она могла быть применена практически ко всему, что есть в мире, от предсказания цен на рынке ценных бумаг до совершения новых открытий в теоретической физике.
Первыми открытыми фракталами были детерминированные фракталы. Их отличительной чертой является свойство самоподобия, обусловленное особенностями метода их генерации.
Некоторые предпочитают называть эти фракталы классическими, геометрическими фракталами или линейными фракталами. Эти фракталы обычно формируются начиная с инициатора — фигуры, к которой применяется определенный основной рисунок. Во всех детерминированных фракталах, самоподобие проявляется на всех уровнях. Это значит, что независимо от того насколько вы приближаете фрактал, вы увидите все тот же узор. Для сложных фракталов, которые будут рассмотрены позже, это не так.
Детерминистские фракталы образуются в процессе, называемом итерацией, которая применяет основной рисунок к инициатору, после чего применяет его к результату и так далее. Большинство людей итерационно повторяют детерминированные фракталы 5-7 раз, чтобы получить четкую красивую картинку. Эти фракталы линейны, так как при каждой итерации что-то убирается, либо что-то прибавляется в форме прямых линий.
Решетка Серпинского. Треугольники, сформированные соединением средних точек большего треугольника вырезаны из главного треугольника, образовывая треугольник, с большим количеством дырочек. В этом случае инициатор — большой треугольник а шаблон — операция вырезания треугольников, подобных большему. Так же можно получить и трехмерную версию треугольника, используя обыкновенный тетраэдр и вырезая маленькие тетраэдры. Размерность такого фрактала ln3/ln2 = 1.584962501 (Рис. 1.31).
Ковер Серпинского. Для получения этого фрактала берут квадрат, делят его на девять квадратов, а средний вырезают. То же самое делают и с остальными, меньшими квадратами. В итоге образуется плоская фрактальная сетка, не имеющая площади, но с бесконечными связями. В своей пространственной форме, губка Серпинского преобразуется в систему сквозных форм, в которой каждый сквозной элемент постоянно заменяется себе подобным. Эта структура очень похожа на разрез костной ткани. Такие повторяющиеся структуры могут стать элементом строительных конструкций. Их статика и динамика, считает Мандельброт, заслуживает пристального изучения (Рис. 1.32).
Фрактал Серпинского. В этом фрактале, инициатор и генератор одинаковы. При каждой итерации, добавляется уменьшенная копия инициатора к каждому углу генератора и так далее. Если при создании этого фрактала произвести бесконечное число итераций, он бы занял всю плоскость, не оставив ни одной дырочки. Поэтому его фрактальная размерность ln9/ln3 = 2.0.
Кривая Коха. Кривая Коха один из самых типичных детерминированных фракталов. Она была изобретена в девятнадцатом веке немецким математиком по имени Хельге фон Кох, который, изучая работы Георга Контора и Карла Вейерштрассе, натолкнулся на описания некоторых странных кривых с необычным поведением. Инициатор — прямая линия. Генератор — равносторонний треугольник, стороны которого равны трети длины большего отрезка. Эти треугольники добавляются к середине каждого сегмента снова и снова. В своем исследовании, Мандельброт много экспериментировал с кривыми Коха, и получил фигуры такие как Острова Коха, Кресты Коха, Снежинки Коха и даже трехмерные представления кривой Коха, используя тетраэдр и прибавляя меньшие по размерам тетраэдры к каждой его грани. Кривая Коха имеет размерность ln4/ln3 = 1.261859507 (Рис. 1.33).
Крест Коха — это один из вариантов кривой Коха, изобретенный Мандельбротом. Вместо отрезка прямой, он использовал в качестве инициатора квадрат или прямоугольник. Так как в этом фрактале использован та же самая идея что и в оригинальной кривой Коха, его фрактальная размерность такая же: ln4/ln3 = 1.261859507 (Рис. 1.34).
Фрактал Мандельброта. Множество Мандельброта основано на нелинейных уравнениях и является комплексным фракталом. Это тоже вариант кривой Коха несмотря на то, что этот объект не похож на нее. Инициатор и генератор так же отличны от использованных для создания фракталов, основанных на принципе кривой Коха, но идея остается той же. Вместо того, чтобы присоединять равносторонние треугольники к отрезку кривой, квадраты присоединяются к квадрату. Благодаря тому, что этот фрактал занимает точно половину отведенного пространства при каждой итерации, он имеет простую фрактальную размерность 3/2 = 1.5 ().
Фрактал Минковского. И инициатор, и генератор довольно сложны и составлены из ряда прямых углов и сегментов различной длины. У самого инициатора 8 частей. Фрактальная размерность колбасы Минковского — ln8/ln4 = 1.5 (Рис. 1.36).
Фрактал Лабиринт. Этот фрактал еще иногда называют H-деревом. И инициатор и генератор имеют вид буквы H. На приведенном здесь примере сама H не закрашена. Вместо этого заполнены области вне фрактала, что облегчает восприятие рисунка и шаблона. Фрактальная размерность этого конкретно фрактала весьма интересна. Так как толщина H в процессе итераций уменьшается, размерность кончиков буквы H точно 2.0, но элементы между кончиками имеют другую размерность, меняющуюся от 1.3333 до 1.6667 (Рис. 1.37).
Пятиугольник Дарера. Фрактал выглядит как связка пятиугольников, сжатых вместе. Фактически он образован при использовании пятиугольника в качестве инициатора и равнобедренных треугольников, отношение большей стороны к меньшей в которых в точности равно так называемой золотой пропорции (1.618033989 или 1/(2cos72)) в качестве генератора. Эти треугольники вырезаются из середины каждого пятиугольника, в результате чего получается фигура, похожая на 5 маленьких пятиугольников, приклеенных к одному большому (Рис. 1.38).
Большая часть встречающихся сегодня фракталов не являются детерминированными. Они н