Для нахождения наибольшего и наименьшего значений (или всего множества значений) данной функции нужно найти ее значения в точках экстремумов и на концах области определения (или заданного промежутка). Исследуем также функцию на монотонность, чтобы обосновать, полученное значение действительно наибольшее или наименьшее.
1. При каких значениях параметра наименьшее значение функции  на отрезке
на отрезке  равно 1? Решение. Наименьшее значение функции на отрезке принимается либо в точке экстремума (для квадратичной функции это вершина параболы), либо на концах отрезка, если вершина лежит вне этого отрезка. Поскольку ветви данной параболы направлены вверх, то, если вершина правее отрезка, то наименьшее значение на правом конце, если вершина левее отрезка, то наименьшее значение на левом конце, если вершина внутри отрезка, то наименьшее значение в вершине. В данном случае абсцисса вершины
равно 1? Решение. Наименьшее значение функции на отрезке принимается либо в точке экстремума (для квадратичной функции это вершина параболы), либо на концах отрезка, если вершина лежит вне этого отрезка. Поскольку ветви данной параболы направлены вверх, то, если вершина правее отрезка, то наименьшее значение на правом конце, если вершина левее отрезка, то наименьшее значение на левом конце, если вершина внутри отрезка, то наименьшее значение в вершине. В данном случае абсцисса вершины  , значит, при
, значит, при  должно быть
должно быть  , при
, при  должно быть
должно быть  , при
, при  должно быть
должно быть  . Решаем три системы: 1)
. Решаем три системы: 1) 
 , 2)
, 2) 


 , 3)
, 3) 
 . Ответ: 2; 0,5.
. Ответ: 2; 0,5. 
2. При каких значениях  наименьшее значение функции
наименьшее значение функции 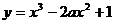 на отрезке
на отрезке  достигается в точке 1? Решение. Найдем производную
достигается в точке 1? Решение. Найдем производную  . Мы видим, что один экстремум функция имеет в точке 0, а второй — в точке
. Мы видим, что один экстремум функция имеет в точке 0, а второй — в точке  . Какой из них — минимум, а какой — максимум, зависит от взаимного расположения этих точек: если
. Какой из них — минимум, а какой — максимум, зависит от взаимного расположения этих точек: если  , то в нуле минимум, и наоборот. Если в точке 0 минимум, то на отрезке
, то в нуле минимум, и наоборот. Если в точке 0 минимум, то на отрезке  значение
значение  — наибольшее. Если
— наибольшее. Если  , то наименьшее значение на отрезке
, то наименьшее значение на отрезке  в точке
в точке  , что тоже не удовлетворяет условию. Только при
, что тоже не удовлетворяет условию. Только при  , наименьшее значение функции на отрезке
, наименьшее значение функции на отрезке  достигается в точке 1. Ответ:
достигается в точке 1. Ответ:  .
.
3. При каких значениях параметра  наибольшее значение функции
наибольшее значение функции  является целым числом? Решение. Преобразуем дробь, разделив числитель на знаменатель:
является целым числом? Решение. Преобразуем дробь, разделив числитель на знаменатель:  . Теперь видно, что наибольшее значение функция имеет в той точке, в которой знаменатель принимает наименьшее значение. Найдем вершину параболы
. Теперь видно, что наибольшее значение функция имеет в той точке, в которой знаменатель принимает наименьшее значение. Найдем вершину параболы  :
:  . Значит, наибольшее значение функции
. Значит, наибольшее значение функции 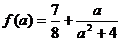 . Найдем множество значений выражения
. Найдем множество значений выражения  с помощью производной (выполните самостоятельно): это отрезок
с помощью производной (выполните самостоятельно): это отрезок  . В этом промежутке есть только одно значение, при котором
. В этом промежутке есть только одно значение, при котором  будет целым:
будет целым:  . Отсюда
. Отсюда 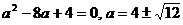 . Ответ:
. Ответ:  .
.
4. При каких значениях  наименьшее значение функции
наименьшее значение функции  на отрезке
на отрезке  отрицательно? Решение. Сделаем замену
отрицательно? Решение. Сделаем замену  и получим функцию
и получим функцию  ,
,  . Преобразуем:
. Преобразуем:  . Данная функция отрицательна в интервале между точками
. Данная функция отрицательна в интервале между точками  и
и  (которая из них больше — неизвестно). Если этот интервал пересекается с отрезком
(которая из них больше — неизвестно). Если этот интервал пересекается с отрезком  , то на этом отрезке есть отрицательные значения, и значит, наименьшее значение отрицательно. Проще найти, при каких значениях
, то на этом отрезке есть отрицательные значения, и значит, наименьшее значение отрицательно. Проще найти, при каких значениях  эти промежутки не пересекаются. При этом либо должна выполняться система
эти промежутки не пересекаются. При этом либо должна выполняться система  , либо система
, либо система  . Т. е. либо
. Т. е. либо  , либо
, либо  . Значит, промежутки пересекаются при
. Значит, промежутки пересекаются при  . Ответ:
. Ответ:  .
.
5. Найти наибольшее значение функции  на отрезке
на отрезке  в зависимости от параметра. Решение. Так как
в зависимости от параметра. Решение. Так как 
 , то при
, то при  функция имеет экстремумы в точках
функция имеет экстремумы в точках 
 , причем в точке
, причем в точке  максимум, а в точках
максимум, а в точках  — минимумы. Значит, наибольшее значение на данном отрезке функция имеет либо в точке
— минимумы. Значит, наибольшее значение на данном отрезке функция имеет либо в точке  , либо на одном из концов. Сравним значения функции в этих точках:
, либо на одном из концов. Сравним значения функции в этих точках:  ,
,  ,
,  . Чтобы выяснить, при каких
. Чтобы выяснить, при каких  какое из этих выражений больше, изобразим графики функций
какое из этих выражений больше, изобразим графики функций 
 ,
,  ,
,  . По чертежу видим, что слева от точки пересечения первой и третьей парабол (при
. По чертежу видим, что слева от точки пересечения первой и третьей парабол (при  большими являются ординаты третьей параболы
большими являются ординаты третьей параболы  . А справа от этой точки большими являются ординаты
. А справа от этой точки большими являются ординаты  . Значит, при
. Значит, при  наибольшее значение функции
наибольшее значение функции  на отрезке
на отрезке  равно
равно  , а при
, а при  оно равно
оно равно  . Ответ: при
. Ответ: при 
 , а при
, а при 
 .
.