Если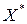 
– оптимальный план, то справедливо равенство:
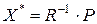
Здесь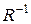 
– подматрица из последней симплекс-таблицы с оптимальным решением (обратная матрица, квадратная). Столбцы этой матрицы располагаются на местах столбцов единичной матрицы первоначального базиса.
Номенклатура продукции сохранится, если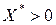 
. Поэтому двойственные оценки различных видов сырья, т.е. оптимальные значения 
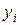, будут устойчивы к изменению запасов ресурсов (не поменяют своих значений), если выполняется условие
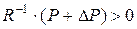
С учетом полученных решений последнее условие примет вид:
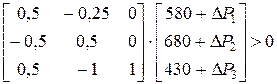
Получим вектор-столбец, каждая компонента которого должна быть строго больше нуля:
(*)
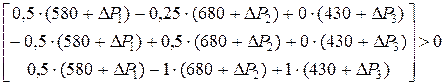Рассмотрим устойчивость двойственных оценок к изменению запасов только первого вида сырья, т.е.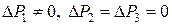 
. Получим:
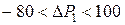
Изменение запасов только второго вида сырья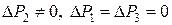 
дает нам следующее:
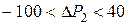
Аналогично, изменение запасов только третьего вида сырья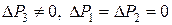 
дает нам следующее:
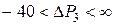
Как и следовало ожидать, произвольное увеличение третьего вида сырья не изменит его нулевой двойственной оценки. При одновременном изменении всех видов сырья,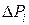 
следует поставить в (*) и проверить условие: каждая компонента вектора-столбца должна быть строго больше нуля.
Устойчивость оптимального плана на изменение стоимости продукции
Изучим вопрос: В каких пределах могут меняться значения коэффициентов целевой функции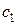 
и 
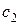, так чтобы оптимальный план оставался неизменным, для рассматриваемого примера 
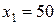и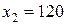 
.
Допустим, значение 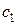изменяется, а значение 
, т.е. фиксировано. При этом вектор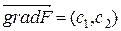 
также изменит направление и величину. В каких пределах может меняться значение , 
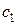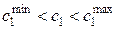, чтобы оптимальный план 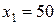и 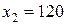оставался неизменным. Изменение значения 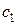приведет к такому расположению линейной формы (целевой функции 
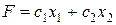), когда линейная форма станет параллельной поочередно сначала одной из прямых, ограничивающих область допустимых решений в оптимальном плане, потом другой, т.е. значение 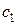изменим таким образом, чтобы линейная форма поочередно стала параллельной двум прямым, на пересечении которых находится оптимальный план. Из условия параллельности прямых, пропорциональности коэффициентов, имеем:
|
|
║ 
.
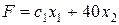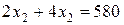Отсюда получим: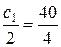 
.
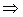
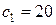Проверяем параллельность линейной формы ко второй прямой, образующей оптимальное решение:
║ 
.
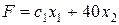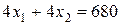Отсюда получим: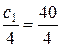 
.
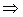
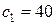Таким образом, значение 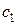меняется в пределах: 
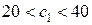, а в задании 
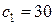. При этом значение целевой функции в оптимальной точке 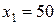и 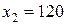меняется в пределах: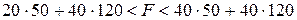 
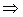
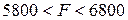, а в задании максимальное значение целевой функции 
.
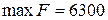Аналогичные результаты можно получить при изменении 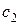с учетом 
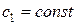. В каких пределах может меняться значение , 
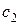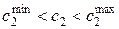, чтобы оптимальный план 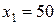и 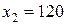оставался неизменным. Значение 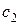изменим таким образом, чтобы линейная форма поочередно стала параллельной двум прямым, на пересечении этих прямых находится оптимальный план. Из условия параллельности прямых, пропорциональности коэффициентов, имеем:
║ .
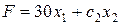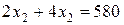Отсюда получим: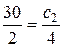 
.
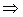
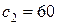Проверяем параллельность линейной формы ко второй прямой, образующей оптимальное решение:
║ .
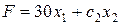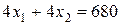Отсюда получим: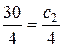 
.
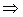
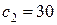Таким образом, значение 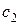меняется в пределах: 
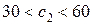, а в задании 
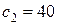. При этом значение целевой функции в оптимальной точке 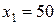и 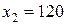меняется в пределах: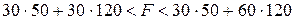 
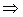
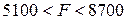, а в задании максимальное значение целевой функции .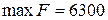