Лабораторная работа №1
Тема: Составление оптимального плана производства
Математическая модель: Задача линейного программирования
Постановка задачи. Предприятие выпускает два вида продукта: 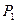 и
и 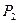 . Для их изготовления используются три вида сырья, запасы которых ограничены и составляют:
. Для их изготовления используются три вида сырья, запасы которых ограничены и составляют: 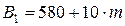 ,
, 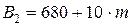 ,
, 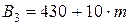 ед. Известны затраты каждого вида сырья на производство единицы каждого вида продукта
ед. Известны затраты каждого вида сырья на производство единицы каждого вида продукта 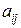 , где
, где 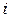 - порядковый номер сырья,
- порядковый номер сырья, 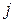 - порядковый номер продукта,
- порядковый номер продукта, 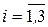 ,
, 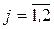 . Значения матрицы
. Значения матрицы 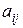 приводятся в нижеследующей таблице:
приводятся в нижеследующей таблице: 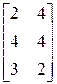 . Требуется составить оптимальный план производства продукции с целью получения максимальной прибыли, если известна прибыль от реализации единицы каждого вида готового продукта
. Требуется составить оптимальный план производства продукции с целью получения максимальной прибыли, если известна прибыль от реализации единицы каждого вида готового продукта 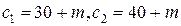 . В задании значение
. В задании значение 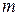 – номер студента по журналу.
– номер студента по журналу.
Построим математическую модель задачи, как задачу ЛП. Пусть 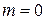
Пусть  – количество выпускаемой продукции вида
– количество выпускаемой продукции вида 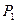 и
и 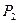 соответственно. Тогда на производство продукции с использованием сырья первого вида запишется в виде
соответственно. Тогда на производство продукции с использованием сырья первого вида запишется в виде 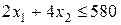 , второго вида
, второго вида 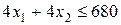 , третьего вида
, третьего вида 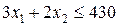 . Это – ограничения по сырьевым ресурсам, запишутся в виде:
. Это – ограничения по сырьевым ресурсам, запишутся в виде: 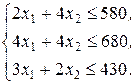
Суммарная прибыль готовой продукции должна быть наибольшей:
 .
.
Для решения задачи симплекс-методом приведем ее к каноническому виду, т.е. ограничения типа неравенства приводятся к ограничениям типа равно путем добавления избыточных переменных 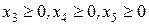 . Избыточная переменная – это количество сырья, которое может остаться в производстве не использованным в излишках:
. Избыточная переменная – это количество сырья, которое может остаться в производстве не использованным в излишках:
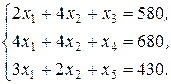
Необходимо требовать условие не отрицательности всех переменных: 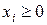 ,
, 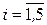 . Целевая функция примет вид:
. Целевая функция примет вид:
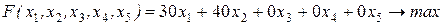
Определяем количество базисных элементов. Количество базисных элементов равно рангу системы ограничений, т.е. числу линейно независимых уравнений в системе. Каждая базисная переменная входит только в одно уравнение системы с коэффициентом 1. В целевой функции базисные переменные отсутствуют. Если ограничения заданной системы до приведения ее в каноническую форму имели вид  , то в качестве первоначальных базисных переменных выбираются избыточные переменные
, то в качестве первоначальных базисных переменных выбираются избыточные переменные  . В других случаях, т.е. когда ограничения типа
. В других случаях, т.е. когда ограничения типа 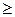 и =, для определения первоначального базиса следует поставить и решить вспомогательную задачу, например, методом искусственного базиса.
и =, для определения первоначального базиса следует поставить и решить вспомогательную задачу, например, методом искусственного базиса.
|
|
Составим первую симплекс – таблицу:
| Базис | X1 | X2 | X3 | X4 | X5 | План | План/X2 |
| X3 | 580/4=145 | ||||||
| X4 | 680/4=170 | ||||||
| X5 | 430/2=215 | ||||||
| F | -30 | -40 |
Последняя строка симплекс – таблицы является оценочной строкой. В этой строке в первоначальной таблице записывают коэффициенты целевой функции с противоположными знаками. Эти коэффициенты называются целевыми оценками. Целевые оценки, соответствующие избыточным переменным 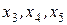 , в оптимальном плане являются оценками ресурсов и характеризуют дефицитность сырья. Целевые оценки должны быть неотрицательными. Если в последней строке имеются отрицательные коэффициенты, то такой план не является оптимальным. Каждая симплекс – таблица соответствует некоторому опорному плану, базисному решению – вершине многоугольника решений. Отправляясь от начального базисного решения, первоначальной симплекс – таблицы, переходят к другому базисному решению, симплекс – таблице с увеличением значения целевой функции вплоть до оптимального.
, в оптимальном плане являются оценками ресурсов и характеризуют дефицитность сырья. Целевые оценки должны быть неотрицательными. Если в последней строке имеются отрицательные коэффициенты, то такой план не является оптимальным. Каждая симплекс – таблица соответствует некоторому опорному плану, базисному решению – вершине многоугольника решений. Отправляясь от начального базисного решения, первоначальной симплекс – таблицы, переходят к другому базисному решению, симплекс – таблице с увеличением значения целевой функции вплоть до оптимального.
|
|
Т.к. в оценочной строке имеются отрицательные коэффициенты, план не является оптимальным. Выбирается столбец с наименьшей оценкой (оценка -40, столбец X2), а затем разрешающий элемент (РЭ) – по наименьшему отношению свободных членов (столбец План) к положительным коэффициентам разрешающего столбца X2. Минимальное отношение находится в строке X3. Таким образом, разрешающий элемент (РЭ) находится на пересечении столбца X2 и строки X3 и равен 4. Далее формируется следующая симплекс – таблица, в которой базисная переменная X3 заменяется переменной X2. Т.к. X2 должна быть базисной переменной, во всех клетках столбца X2 должны быть 0 кроме клетки на пересечении со строкой X3 (клетки с РЭ), где должна быть 1. Все элементы разрешающей строки разделим на РЭ (4). Все остальные элементы новой симплекс – таблицы, включая и строку с целевыми оценками, определяются по правилу прямоугольника. Для этого выбираются из старой симплекс – таблицы четыре числа, которые расположены в вершинах прямоугольника, всегда включая при этом разрешающий элемент (РЭ):
НЭ=СЭ – (А*В)/РЭ,
где НЭ – новый элемент, СЭ – элемент старого плана, РЭ – разрешающий элемент (4), А и В – элементы старого плана, образующие прямоугольник с элементами СЭ и РЭ. Расчет каждого элемента можно представить в виде таблицы:
| Базис | X1 | X2 | X3 | X4 | X5 | План |
| X2 | 2/4 | 4/4 | 1/4 | 0/4 | 0/4 | 580/4 |
| X4 | 4-(2*4)/4 | 0-(4*1)/4 | 1-(4*0)/4 | 0-(4*0)/4 | 680-(4*580)/4 | |
| X5 | 3-(2*2)/4 | 0-(2*1)/4 | 0-(2*0)/4 | 1-(2*0)/4 | 430-(2*580)/4 | |
| F | -30-(-40*2)/4 | 0-(-40*1)/4 | 0-(-40*0)/4 | 0-(-40*0)/4 | 0-(-40*580)/4 |
Новая симплекс таблица примет вид:
| Базис | X1 | X2 | X3 | X4 | X5 | План | План/X1 |
| X2 | 0,5 | 0,25 | 145/0,5=280 | ||||
| X4 | -1 | 100/2=50 | |||||
| X5 | -0,5 | 140/2=70 | |||||
| F | -10 |
Полученный план не является оптимальным, т.к. в целевой строке присутствует отрицательный коэффициент (-10). Формируется новая симплекс – таблица, в которой базисной переменной должна стать X1.Разрешающий элемент определяется по наименьшему отношению свободных членов (столбец План) к положительным коэффициентам разрешающего столбца X1. Минимальное отношение находится в строке X4 и равно 50. Таким образом, разрешающий элемент (РЭ) находится на пересечении столбца X1 и строки X4 и равен 2. Далее базисная переменная X4 заменяется переменной X1, во всех клетках столбца X1 записываются 0 кроме клетки на пересечении со строкой X4 (клетки с РЭ), где должна быть 1. Все элементы разрешающей строки разделим на РЭ (2). Все остальные элементы новой симплекс – таблицы, включая и строку с целевыми оценками, определяются по правилу прямоугольника Расчет каждого элемента можно представить в виде таблицы:
|
|
| Базис | X1 | X2 | X3 | X4 | X5 | План |
| X2 | 0,5 | 1-(0*0,5)/2 | 0,25-(-1*0,5)/2 | 0-(1*0,5)/2 | 0-(0*0,5)/2 | 145-(100*0,5)/2 |
| X1 | 2/2 | 0/2 | -1/2 | 1/2 | 0/2 | 100/2 |
| X5 | 0-(2*0)/2 | -0,25-(-1*2)/2 | 0-(2*1)/2 | 1-(0*2)/2 | 140-(2*100)/2 | |
| F | -10 | 0-(-10*0)/2 | 10-(-10*(-1))/2 | 0-(-10*1)/2 | 0-(-10*0)/2 | 5800-(-10*100)/2 |
Новая симплекс – таблица примет вид:
| Базис | X1 | X2 | X3 | X4 | X5 | План |
| X2 | 0,5 | -0,25 | ||||
| X1 | -0,5 | 0,5 | ||||
| X5 | 0,5 | -1 | ||||
| F |
Последняя симплекс таблица дает нам оптимальный план, т.к. в целевой строке все коэффициенты больше или равно нулю.
Таким образом, оптимальный план следующий:
X1=50; X2=120. При этом максимальная прибыль равна 6300. Значения переменных X3 и X4 равны нулю, т.е. сырье первого и второго вида полностью израсходованы. Сырье третьего вида оказался не израсходованным полностью, в остатке X4=40. В целевой строке последней симплекс – таблицы мы также получили оценки ресурсов: Оценка первого вида ресурса равна 5, второго вида – 5, третьего вида – 0. Оценки ресурсов – это количество прибыли, которую можно получить с единицы сырья.
Двойственная задача
Припишем единице каждого 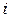 - го вида сырья оценку
- го вида сырья оценку 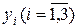 . Эти оценки должны удовлетворять следующим условиям:
. Эти оценки должны удовлетворять следующим условиям:
1) Общая оценка количества всех видов сырья, используемых в производстве должна быть минимальной:
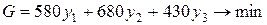
2) Суммарная оценка всех видов сырья, расходуемого на выпуск единицы продукции любого вида, должна быть не ниже прибыли от реализации единицы продукции данного вида. В противном случае предприятие откажется от выпуска данного вида продукции. Оценка сырья – это количество прибыли, которую можно получить с единицы сырья. Математически ограничения двойственной задачи можно записать в следующем виде:
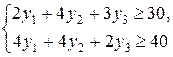
3) Оценки 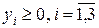 .
.
Можно решать прямую задачу на получение максимальной прибыли или двойственную на минимизацию общей стоимости имеющегося сырья. Обе задачи, прямая и двойственная, тесно связаны между собой, поэтому решение одной из них без особого труда можно определить, если известно решение другой. Самостоятельно проверить связи между прямой и двойственной задачами. Решение двойственной задачи находится в индексной строке последней симплекс-таблицы в столбцах, соответствующих избыточным переменным 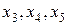 . Таким образом, решение двойственной задачи, оптимальное значение двойственных оценок равно:
. Таким образом, решение двойственной задачи, оптимальное значение двойственных оценок равно: 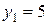 ,
, 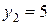 ,
, 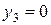 . Минимальная оценка количества всех видов сырья
. Минимальная оценка количества всех видов сырья 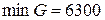 .
.