Домашнее задание по линейной алгебре
К занятию 1, модуль 2
Специализация «Мировая экономика»
1. Докажите линейность следующих операторов по определению, найдите их матрицы в базисе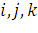 
, а также образ, ядро, ранг и дефект оператора:
а) оператор проецирования пространства геометрических векторов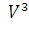 
на плоскость Oxz;
б) оператор отражения пространства геометрических векторов 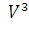относительно плоскости Oxz;
в) оператор поворота геометрических векторов из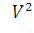 
на угол 
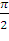против хода часовой стрелки;
г) оператор поворота геометрических векторов из 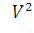на угол 
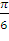против хода часовой стрелки;
д) оператор отражения геометрических векторов из 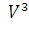относительно плоскости 
;
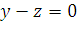е) оператор проецирования геометрических векторов из 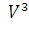на плоскость 
;
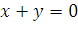2. Докажите линейность оператора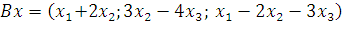 
. Составьте его матрицу в данном базисе.
3. Линейный оператор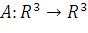 
в некотором базисе задан матрицей
.
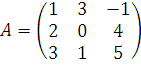а) найдите ранг и дефект оператора;
б) найдите базис в образе оператора;
в) найдите базис в ядре оператора.
4. Линейный оператор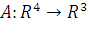 
в некотором базисе задан матрицей
.
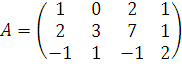а) найдите ранг и дефект оператора;
б) найдите базис в образе оператора;
в) найдите базис в ядре оператора.
5. Линейный оператор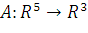 
в некотором базисе задан матрицей
.
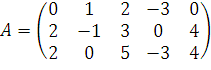а) найдите ранг и дефект оператора;
б) найдите базис в образе оператора;
в) найдите базис в ядре оператора.
6. Линейный оператор 
в некотором базисе задан матрицей
.
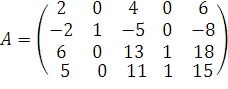а) найдите ранг и дефект оператора;
б) найдите базис в образе оператора;
в) найдите базис в ядре оператора.
7. В некотором базисе трехмерного линейного пространства заданы линейные операторы
, 
.
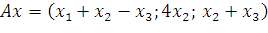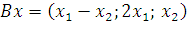Найдите координаты вектора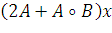 
в том же базисе.
8. В некотором базисе s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:b/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/><w:lang w:val="RU"/></w:rPr><m:t>3</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">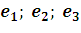 
задан произвольный вектор 
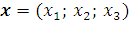и его образ 
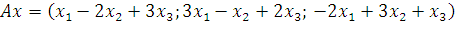. Найдите координаты вектора 
.
|
|
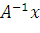9. В некотором базисе трехмерного линейного пространства заданы линейные операторы
, 
.
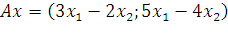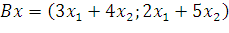Найдите матрицы операторов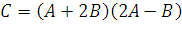 
и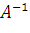 
в том же базисе, в котором даны координаты векторов 
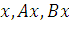. Векторы 
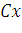и 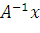запишите в координатной форме.
10. В базисе 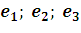задан вектор 
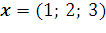. Найдите координаты этого вектора в базисе
; 
; 
.
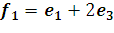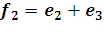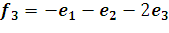11. Линейный оператор A в базисе 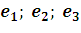матрицу 
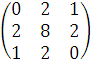. Найдите матрицу этого оператора в новом базисе
; 
; 
.
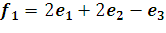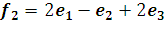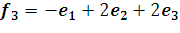12. В базисе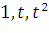 
запишите матрицу оператора дифференцирования многочленов степени, меньшей или равной 2. Используя матрицу перехода, найдите матрицу оператора в базисе 
.
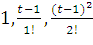13. Найдите матрицу линейного оператора, переводящего векторы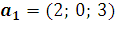 
, 
, 
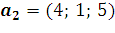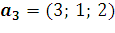в векторы 
, 
, 
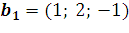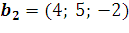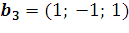в том же базисе, в коротом даны векторы.
14. Найдите матрицу линейного отображения, переводящего векторы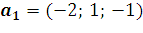 
, 
, 
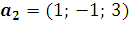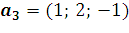в векторы 
, 
, 
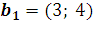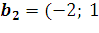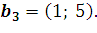
15. Могут ли матрицы А и В быть матрицами одного и того же линейного оператора в разных базисах, если
, 
?
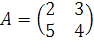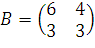16. Найдите координаты вектора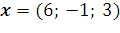 
в базисе s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:b/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/><w:lang w:val="RU"/></w:rPr><m:t>3</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
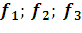, если он задан в базисе s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:b/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/><w:lang w:val="RU"/></w:rPr><m:t>3</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 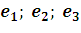, при этом
|
|
; 
; 
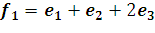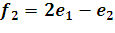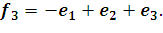
17. Найдите матрицу перехода от базиса 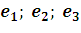к базису s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:b/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/><w:lang w:val="RU"/></w:rPr><m:t>3</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 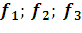в трехмерном линейном пространстве и определите координаты вектора 
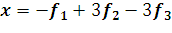в базисе s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:b/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/><w:lang w:val="RU"/></w:rPr><m:t>3</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 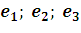, если
|
|
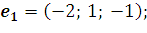
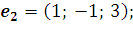
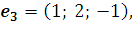
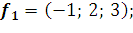
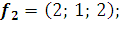
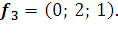
18. Дана система линейных однородных уравнений:
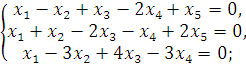а) 
а)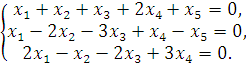 
Найти фундаментальную систему решений и общее решение этой системы уравнений. Считая, что линейный оператор А задан своей матрицей, совпадающей с матрицей данной СЛАУ, найти базис в ядре оператора А и описать векторы, составляющие ядро.