2.2.1 Рассчитать и построить распределения напряжения вдоль разомкнутой на конце линии длиной l = 1000 км, присоединенной в первом случае к источнику с нулевым внутренним сопротивлением X и = 0 (источник бесконечной мощности), а во втором – к источнику с внутренним сопротивлением X и = 0,5 Z c.
2.2.2 Рассчитать и построить зависимости напряжения в конце разомкнутой линии от ее длины U к / E = f (l) при источнике с нулевым внутренним сопротивлением в первом случае и при источнике с внутренним сопротивлением X и = 0,5 Z c – во втором. Зависимости построить в диапазоне длин от 0 до 2000 км.
2.2.3 В начале линии длиной l = 1000 км подключен источник с нулевым внутренним сопротивлением, а в конце линии – шунтирующий реактор мощностью q р = 0,5 (см. рисунок 16). Определить, на каком расстоянии от начала линии l 0 меняется характер тока в линии с емкостного на индуктивный. Потерями в линии пренебречь. Индуктивное сопротивление ректора определяется по формуле X р = Z c/ q р.
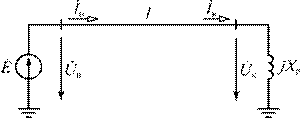
Рисунок 16 – Линия электропередачи с шунтирующим реактором в конце
2.2.4 Для п.2.2.3. определить, при какой мощности шунтирующего реактора q р напряжения в начале и в конце линии равны (см. рисунок 16).
2.2.5 Рассчитать емкостное сопротивление устройства продольной компенсации X c (подключенного в рассечку в середине линии) необходимое для обеспечения равенства напряжений в начале U н1 и в конце линии U к2. В начале линии подключен источник с нулевым сопротивлением, а в конце линия разомкнута (см. рисунок 17). Длина линии равна l = 1000 км. Потерями в линии пренебречь.

Рисунок 17 – Линия электропередачи с устройством продольной компенсации
Задание на измерения
При выполнении лабораторной использовать такие же значения погонных параметров линии, как и при выполнении предварительной подготовки. Потери учитывать во всех пунктах.
2.3.1 Измерить и построить кривые распределения напряжения U (x) / E = f (x) вдоль разомкнутой линии длиной l = 1000 км для случаев источника с нулевым внутренним сопротивлением X и = 0 и источника с внутренним сопротивлением X и = 0,5 Z c.
2.3.2 Повторить опыт п.2.3.1 для линии длиной l = 2000 км.
2.3.3 Измерить и построить зависимости напряжения в конце разомкнутой линии от ее длины U к / E = f (l) для случаев источника с нулевым внутренним сопротивлением X и = 0 и источника с внутренним сопротивлением X и = 0,5 Z c. Зависимости построить в диапазоне длин от 0 до 2000 км. Индуктивность источника определяется по формуле L и = X и/(100 π).
2.3.4 Для п.2.2.4 предварительной подготовки измерить и построить распределение напряжения U (x) / E = f (x) вдоль линии с шунтирующим реактором в конце.
2.3.5 Для п.2.2.5 предварительной подготовки измерить и построить распределение напряжения U (x) / E = f (x) вдоль линии с устройством продольной компенсации.
2.3.6 Измерить и построить кривые распределения напряжения U (x) / E = f (x) вдоль разомкнутой линии длиной l = 1000 км, присоединенной к источнику с внутренним сопротивлением X и = 0,5 Z c, с различным расположением реакторов поперечной компенсации:
a) реактор мощностью q р = 1 в начале линии;
b) реактор мощностью q р = 1 в конце линии;
c) реактор мощностью q р = 1 в середине линии;
d) реакторы мощностью q р = 0,7 в начале и q р = 0,6 в конце линии;
e) реакторы мощностью q р = 0,275 в начале и в конце, реактор мощностью q р = 0,525 в середине линии.
Индуктивность реактора определяется по формуле L р = Z c/(100 πq р).
2.3.7 Каковы условия возникновения резонанса для линии, присоединенной к источнику с нулевым внутренним сопротивлением и с индуктивным внутренним сопротивление?
2.3.8 Определить значение мощности шунтирующего ректора, необходимой для полной компенсации емкостного тока в начале линии при включении реактора в начале, конце и середине линии?