4.2.3.2 Принцип резолюции для логики предикатов
Поскольку в логике предикатов внутри предикатов содержатся переменные, то алгоритм доказательства несколько изменяется. В этом случае, перед тем как применить описанный алгоритм, будет проведена некоторая подстановка в переменные и вводится понятие унификации с помощью этой подстановки. Унификацию проиллюстрируем следующим простым примером.
Рассмотрим два предиката – L(x) и L(a). Предположим, что x – переменная, a - константа. В этих предикатах предикатные символы одинаковы, чего нельзя сказать о самих предикатах. Тем не менее подстановкой a в x одинаковыми (эта подстановка и называется унификацией).
Целью унификации является обеспечение возможности применения алгоритма доказательства для предикатов. Например, предположим имеем:
В данном случае L(x) и 
не находятся в дополнительном отношении. При подстановке a вместо x будут получены, соответственно, 
и , и поскольку эти предикаты отличаются только символами отрицания, то они находятся в дополнительном отношении. Однако, операцию подстановки нельзя проводить при отсутствии каких-либо ограничений.
Подстановку t в x принято записывать как {t/x}. Поскольку в одной ППФ может находиться более одной переменной, можно оказаться необходимо провести более одной подстановки. Обычно эти подстановки записываются в виде упорядоченных пар {t1/x1, …, tn/xn}.
Условия, допускающие подстановку:
- xi – является переменной,
- ti – терм (константа, переменная, символ, функция) отличный от xi,
- для любой пары элементов из группы подстановок, например (ti/xi и tj/xj) в правых чачтях символов / не содержится одинаковых переменных.
Унификация
Обозначим группу подстановок {t1/x1, …, tn/xn} через q. Когда для некоторого представления L применяется подстановка содержащихся в ней переменных {x1, …, xn}, то результат подстановки, при которой переменные заменяются соответствующими им термами t1, …, tn принято обозначать Lq.
Если имеется группа различных выражений на основе предиката L, то есть L1, …, Lm}, то подстановка q, такая, что в результате все эти выражения становятся одинаковыми, то есть L1q = L2q = … = Lmq, q - называется унификатором {L1, …, Lm}. Если подобная подстановка q существует, то говорят, что множество {L1, …, Lm} унифицируемо.
Множества {L(x), L(a)} унифицируемо, при этом унификатором является подстановка (a/x).
Для одной группы выражений унификатор не обязательно единственный. Для группы выражений {L(x, y), L(z, f(x)} подстановка q = {x/z, f(x)/y} является унификатором, но является также унификатором и подстановка q = {a/x, a/z, f(a)/y}. Здесь a – константа, x – переменная. В таких случаях возникает проблема, какую подстановку лучше выбирать в качестве унификатора.
Операцию подстановки можно провести не за один раз, а разделив ее на несколько этапов. Ее можно разделить по группам переменных, проведя, например, подстановку {t1/x1, t2/x2, t3/x3, t4/x4} сначала для {t1/x1, t2/x2}, а затем для {t3/x3, t4/x4}. Допустимо также подстановку вида a/x разбить на две подстановки u/x и a/u. Результат последовательного выполнения двух подстановок q и l также подстановка и обозначается l°q.
Если существует несколько унификаторов, то среди них непременно найдется такая подстановка s, что все другие унификаторы являются подстановками, выражаемыми в виде s°l, как сложная форма, включающая эту подстановку. В результате подстановки переменные будут замещаться константами и описательная мощность ППФ будет ограничена.
Чтобы унифицировать два различных выражения предиката, необходима такая подстановка, при которой выражение с большей описательной мощностью согласуется с выражением с меньшей описательной мощностью. Такую подстановку принято называть «наиболее общим унификатором» (НОУ). Метод отыскания НОУ из заданной группы предикатов выражений называется алгоритмом унификации.
Этот алгоритм состоит в том, что сначала упорядочиваются выражения, которые подлежат унификации. Когда каждое выражение будет упорядочено в алфавитном порядке, среди них отыскивается такое, в котором соответствующие термы не совпадают межде собой.
Положим, что при просмотре последовательно всех выражений в порядке слева направо несовпадающими термами оказались x, t. Например, получено {L(a, t, f(z)), L(a, x, z)}. В этом случае, если:
1. x является переменной;
2. x не содержится в t, к группе подстановок добавляется {t/x}.
Если повторением этих операций будет обеспечено совпадение всех изначально заданных выражений, то они унифицируемы, а группа полученных подстановок является НОУ.
В приведенном примере третий терм в одном случае z, а в другом – f(z), первое условие выполняется, а второе – нарушается. Поэтому подстановка недопустима. Если в группе предикатных выражений остается хотя бы одно такое, для которого никакими подстановками нельзя получить совпадения с другими выражениями, такая группа называется неунифицируемой.
Рассмотрим другой пример:
P1 = L(a, x, f(g(y))),
P2 = L(z, f(z), f(u)).
1. Первые несовпадающие члены: {a, z}.
Подстановка: a/z. Имеем:
P1 = L(a, x, f(g(y))),
P2 = L(a, f(a), f(u)).
2. Первые несовпадающие элементы {x, f(a)}. Подстановка: [f(a)/x]. Имеем:
P1 = L(a, f(a), f(g(y))),
P2 = L(a, f(a), f(u)).
3. Первые несовпадающие элементы {g(y), u}. Подстановка: [g(y)/u]. Получаем совпадение. Следовательно, НОУ: [a/z, f(a)/x, g(y)/u].
Алгоритм доказательства
Пусть заданы:
Предикаты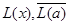 
делаются дополнительными с помощью подстановки [a/x]. Суждение о том, становятся ли два выражения дополнительными, выносится:
1. По различию используемых символов.
2. По существованию НОУ для двух выражений, в которых удалены одинаковые символы.
Далее все делается рекуррентно.
Пример 1. Милиция разыскивает всех въехавших в страну, за исключением дипломатов. Шпион въехал в страну. Однако, распознать шпиона может только шпион. Дипломат не является шпионом.
Оценим вывод: среди милиционеров есть шпион.
Воспользуемся следующими предикатами:
Въехал(x): x въехал в страну.
Дипломат(x): x – дипломат.
Поиск(x, y): x разыскивает y.
Милиционер(x): x – милиционер.
Шпион(x): x – шпион.
Если выразим через эти предикаты посылку и вывод в форме ППФ, то получим:
для всех x, если x не является дипломатом, но въехал в страну, найдется милиционер y, который его разыскивает.
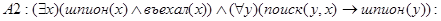
Если существует шпион x, который въехал в страну, и некоторый y разыскивает его, то он сам шпион.
Для всех x справедливо, что если x является шпионом, то он не дипломат.
Заключение:
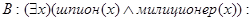
Существует x такой, что он является шпионом и милиционером.
Если эти формулы преобразовать в клаузальную нормальную форму, то получим:
Заключение преобразуем в свое отрицание:
и затем в клаузальную форму без квантора общности.
Последующий процесс доказательства имеет вид:
дипломат(а)Úмилиционер(f(а)) [a/x] из 2,4 (9)
милиционер(f(а)) [a/x] из 8,9 (10)
дипломат(а)Úпоиск(f(а),а) [a/x] из 1,4 (11)
поиск(f(а),а) [a/x] из 8,11 (12)
шпион(f(a)) [a/x] из 12,5 (13)
ð [f(a)/x)] из 10 и 14 (15)
Еще одной возможностью метода резолюции является возможность получать конкретные значения переменных, содержащихся в заключении.
4.2.3.3 Задачи, использующие равенства
Новые предложения получались до сих пор двумя способами: подстановкой и резолюцией. При резолюции пары предложений, отображаются в новые предложения, а подстановка заменяет терм в предложении другим термом той же синтаксической формы. Иногда возникает необходимость заменить терм равным ему термом, который не является термом, для которого возможна подстановка (подстановочным случаем) в первом терме. Рассмотрим простой пример. Положим f(x, y) = x + y. При сравнении предложений:
у нас нет способа обнаружить противоречие, поскольку резолюция не допускает замены термов разных синтаксических форм. Поэтому имеет смысл, включить в программу, использующую принцип резолюции, специальные правило вывода, которое должно применяться, когда возникает необходимость в операции равенства. Чтобы это правило было совместимо с остальной частью программы, оно должно удовлетворять двум условиям:
1. Работать с предложениями, в которых равенство выражено в виде атомов.
2. Быть операцией, превращающей два предложения в третье.
Это специальное правило вывода называется парамодуляцией.
Пусть A, B и т.д. будут множествами литералов, а a, b, g - термами, то есть константами, переменными или функциональными выражениями. В дополнении к обычному определению атомов и литералов будем записывать атомы равенства в виде a=b (терм a равен терму b). К таким термам можно применять подстановку.
Правило парамодуляции
Если для заданных предложений C1 и C2 = (a’ = b’, B) ( или C2’ = (b’ = a’, B)), не имеющих общих переменных в общей части B выполняются условия:
1. C1 содержит терм d.
2. У d и a’ есть наиболее общий унификатор:
,
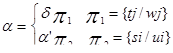где ui и wj – переменные соответственно из a’ и d,
то надо построить предложения 
= C1p1, а затем C#, заменяя a’ на b’p2 для какого-то одного вхождения a’ в C1*. Наконец вывести:
C3=(C#, Bp).
Формулировка весьма сложна, но ее реализация очень проста. В простейшем случае B пусто, так что предложения, содержащие высказывания с равенством, состоят из единственного атома выражающего равенство. Таким образом, из:
C1={Q(a)},
C2={a=b}
можно вывести:
C3={Q(b)}.
Несколько более сложный случай:
C1={Q(x)},
C2={(a=b)}.
Подстановка p = (a/x) дает:
C1*={Q(a)},
C3={Q(b)}.
При одном применении парамодуляции подстановка a=bp2 применяется в С1* только один раз. Таким образом, если заданы предложения:
C1={Q(x), P(x)},
C2={(a=b)},
то одно применение парамодуляции с подстановкой p = (a/x) дает сначала
C1*={Q(a), P(a)},
а затем или
C3={Q(a),P(b)},
либо
C3={Q(b), P(a)}.
Для получения C4={Q(b), P(b)} требуется повторное применение парамодуляции.
Рассмотрим пример по сюжету известной сказки Андерсона «Принцесса на горошине», который может служить тестом на наличие королевской крови.
Определения для примера:
1. x, y, z – переменные, принимающие значения на множестве людей.
2. M(x): x – мужчина.
3. C(x): x – простолюдин.
4. D(x): x может почувствовать горошину через перину.
5. x = k: x – король.
6. x = q: x – королева.
7. d(x,y): дочь x и y.
8. x = p: x – принцесса.
Исходные предложения:
- существует мужчина.
- существует женщина.
- любой мужчина не простолюдин король.
- любая королева – женщина и не простолюдинка.
- дочь короля и королевы – принцесса.
- принцесса может почувствовать горошину.
Удалим квантор существования из предложений C1, C2, обозначив через f1, f2 сколемовские функции без переменных, так как перед квантором существования нет квантора общности.
: f1 – мужчина.
f2 – женщина.
Опускаем кванторы всеобщности в C3, C4. Проводим резолюцию C1 с C3, а затем C2 и C4. Получаем:
f1 – король или простолюдин.
f2 – королева или простолюдинка.
Затем осуществляем парамодуляцию C7 и C5. Это дает:
дочь королевы и f1 – есть принцесса или f1 - простолюдин. Затем осуществляем парамодуляцию C8 и C9. Это дает:
дочь f1 и f2 есть принцесса, либо f1, либо f2 – простолюдин. Наконец парамодуляция C10 с C6 дает:
дочь f1 и f2 может почувствовать горошину, либо f1, либо f2 – простолюдин.
4.2.4 Стратегии очищения
Применение принципа резолюции без ограничений может привести к слишком большому количеству предложений, чтобы с ним можно было бы работать на практике. Поэтому надо уметь заранее определять, какие выполнять резолюции и какие производить выводы. На этом и основываются стратегии очищения.
4.2.4.1 Стратегия предпочтения одночленов
В стратегии предпочтения одночленов требуется, чтобы на каждом шаге вывода все резолюции, использующие предложения только с одним литералом, вычислялись прежде других резолюций. В общем случае резолюции, использующие короткие предложения, выполняются перед резолюциями с более длинными предложениями. Эта стратегия скорее относится к упорядочиванию, а не к очищению, так как она меняет лишь порядок выполнения, но ни одну из возможных резолюций не исключает из рассмотрения.
4.2.4.2 Факторизация
Размер предложений по длине можно уменьшить, используя подстановки, так что некоторые литералы в предложении становятся одинаковыми. Эта операция называется факторизацией. Например:
C = {A(x, f(k)), A(b, y), A(a, f(x)), A(x, z)}
можно факторизовать подстановкой:
q =(b/x, f(k)/y, f(b)/z).
Тогда получим:
Cq = {A(b, f(k)), A(a, f(b)), A(b, f(b))}.
Cq называется факториалом предложения C. Фактор предложения не обязательно единственный. Другой фактор:
p = (a/x, f(k)/y, f(a)/z),
Cp = {A(a, f(k)), A(b, f(k)), A(a, f(a)}.
4.2.4.3 Использование подслучаев
Для любой пары предложений C, D Î S предложение C называется подслучаем предложения D, если существует такая подстановка p, что Cp Í D. Например:
C = {A(x)},
D = {A(b), P(x)},
то подстановка
p = (b/x)
приведет к
Cp = {A(b)}.
то означает сокращение литералов.
4.2.4.4 Гиперрезолюция
Можно делать так, чтобы в резолюции участвовали сразу по несколько предложений. Это называется гиперрезолюцией. Предположим, что для конечного множества предложений {C1, …, Cn} и единственного предложения B удовлетворяются следующие условия:
1. B содержит n литералов L1, …, Ln.
2. Для каждого i, 1£ i £ n, предложение Ci, содержит литерал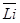 
, но не содержит дополнений никакого другого литерала из B и никакого литерала из любого предложения Cj, j ¹ i.
Множество Sa = {Ci} È {B} будем называть конфликтом, а предложение:
его гиперрезольвентой. Ra можно вывести из Sa.
В большинстве случаев к конфликту приходят после соответствующих подстановок. Иными словами, для заданного множества предложений Sa, не удовлетворяющего определению конфликта, может найтись такая подстановка p, что Sap будет конфликтом. Тогда Sa называется скрытым конфликтом.
В качестве примера гиперрезолюции рассмотрим множества:
Подстановка p =(a/x, b/y) дает
Sap - конфликт с резольвентой 
, и Sa – скрытый конфликт.
4.2.4.5С – упорядочение
С – упорядочение предполагает линейность, так как при его определении различаются левое и правое родительские предложения. Пусть С – предложение из S. Обозначим через [C] предложение C с заданным на нем произвольным порядком литералов, а через [S] – множество таких упорядоченных предложений. Если предложение [C] порождается в линейном выводе 
то пусть [Ci-1] и [Bi-1] будут его левым и правым предложениями с литералами предложения Ci-1, расположенными в порядке 
(где 
т.е. самый правый литерал левого родительского выражения является литералом резолюции), и с литералами предложения Bi-1 в порядке 
. Ясно, что для 
некоторого i (i =1¸m). Тогда упорядоченное предложение Ci таково:
т.е. литералы правого родительского предложения добавляются к литералам левого, при этом литералы резолюции, естественно, опускаются, а в случае повторения литералов сохраняются те, что расположены слева. Резолюция допускается только с самым правым литералом предложения Ci.
Пример:
Компьютерный практикум
Реализовать алгоритм C – упорядочивания.