4.2.1 Неаксиоматическое описание процедуры
В логике предикатов используется формальный метод доказательства теорем, допускающий возможность его машинной реализации. Но для упрощения рассмотрим сначала процедуру доказательства неаксиоматическим путем.
Пусть в качестве å задана группа логических формул следующего вида:
Отец(x, y): x является отцом y;
Брат(x, y): x, y – братья;
Кузен(x, y): x, y – двоюродные братья;
Дедушка(x, y): x – дедушка y.
Используя эти предикаты можно записать следующие утверждения:
(1) ("x1)("y1)("z1)((отец(x1, y1) Ù отец(y1, z1)) ® дедушка(x1, z1)):
если x1 отец y1, а y1 отец z1, то x1 дедушка z1.
(2) ("x2, y2, z2, w2)((отец(x2, y2) Ù брат(x2, z2) Ù отец(z2, w2)) ® кузен(y2, w2)).
(3) ("x3, y3, z3)((отец(x3, y3) Ù отец(x3, z3) Ù 
) ® брат(y3, z3)).
Предположим также, что помимо этих логических формул заданы следующие факты:
(4) Отец(Александр, Сергей),
(5) Отец(Сергей, Ричард).
(6) Отец(Сергей, Иван).
Сначала неаксиоматически зададим процедуру, которая из логических формул выводит заключение. Вывод формулы C из логических формул A, B будем задавать в виде схемы:
А: Все люди смертны
В: Сократ – человек
С: Сократ – смертен.
Если в переменную подставляется значение, то слева от наклонной черты запишем имя переменной, а справа – значение. Например, если в переменную x подставляется значение Сократ, то будем это записывать как x/Сократ.
Предположим, теперь, что требуется доказать – истинна или ложна логическая формула. В ее истинности или ложности можно убедиться логической процедурой, применив ранее заданные логические формулы. Эта процедура выглядит аналогично процедуре доказательства теорем, когда выдвигается некоторая теорема, а справедливость ее устанавливается из известных аксиом.
Например, предположим, что задан вопрос: «Кто дедушка Ричарда?». Его можно записать в виде:
($x)(дедушка(x, Ричарда)).
Ответ может быть получен в следующей последовательности:
Поскольку заключение получается из комбинации уже существующих правил, ответ является результатом процедуры восходящего вывода.
С другой стороны можно осуществить и нисходящий вывод. Нисходящий вывод начинается с того заключения, которое должно быть получено, и далее в базе проводится поиск информации, которая последовательно позволяет прийти к данному заключению.
В логике предикатов такая процедура полностью формализована и носит название метода резолюции.
Для применения этого метода исходную группу логических формул преобразуют в нормальную форму. Преобразование проводится в несколько стадий.
4.2.2 Процесс нормализации
4.2.2.1Префиксная нормальная форма
Рассмотрим фразу «любой человек имеет отца». Ее можно представить в логике предикатов в следующем виде:
("x)(человек(x) ® ($y)(отец(y, x))).
$ находится внутри ППФ. Это не всегда удобно, поэтому целесообразно вынести все кванторы за скобки, чтобы они стояли перед ППФ. Такая форма носит название префиксной нормальной формы.
Преобразование к префиксной нормальной форме произвольной ППФ можно легко выполнить машинным способом, используя для этого несколько простых правил.
Во-первых, необходимо исключить связки ® и ». По определению:
Следовательно, во всех комбинациях ППФ можно ограничиться тремя связками Ú, Ù и `.
Предикат, не содержащий переменных, аналогичен высказыванию, поэтому такие предикаты будем обозначать F, G. Когда некоторое выражение выполняется для любого квантора " и $ будем записывать такой квантор Q.
Легко показать:
1. 
Это соответствует: высказывание не имеет отношения к квантору переменной, которая включена в другой предикат.
Между предикатами существует следующее соотношение:
Таким образом, «необязательно F(x) выполняется для всех x » º «существует такое x, что F(x) не выполняется»; «не существует такое x, что выполняется F(x) » º «для всех x не выполняется F(x) ».
Далее имеем:
2. ("x)F(x)Ù("x)H(x) = ("x)(F(x)ÙH(x))
($x)F(x)Ú($x)H(x) = ($x)(F(x)ÚH(x)).
Это означает, что квантор " обладает дистрибутивностью относительно Ù, а $ - относительно Ú.
С другой стороны:
("x)F(x)Ú("x)H(x)¹("x)(F(x)ÚH(x)).
($x)F(x)Ù($x)H(x)¹($x)(F(x)ÙH(x)).
Это легко показать. Пусть для первого выражения x определен на множестве D ={а, б, в}, при этом истиной являются F(а), F(б), H(в). Тогда левая часть не выполняется, а правая истинна. На самом деле справедливо:
("x)F(x)Ú("x)H(x)®("x)(F(x)ÚH(x)).
($x)F(x)Ù($x)H(x)®($x)(F(x)ÙH(x)).
Смысл этих формул в том, что описание для двух разделенных предикатов не совпадает с описанием, использующим эти предикаты одновременно как одно целое и с одинаковыми переменными. Поэтому, изменив все переменные в их правых частях, получим:
("x)F(x)Ú("x)H(x) = ("x)F(x) Ú ("y)H(y),
($x)F(x) Ù($x)H(x) = ($x)F(x) Ù ($y)H(y).
Теперь H(y) не содержит переменной x и поэтому не зависит от связывания x. Отсюда:
3. ("x)F(x)Ú("x)H(x) = ("x)("y)(F(x) Ú H(y)),
($x)F(x) Ù($x)H(x) = ($x)($y)(F(x) Ù H(y)).
Таким образом, процесс получения префиксной нормальной формы можно представить как последовательность шагов:
1. Используя формулы для ®, », заменим их на Ù, Ú, ¾.
2. Воспользовавшись выражениями
внесем отрицания внутрь предикатов.
3. Вводятся новые переменные, где это необходимо.
4. Используя 1, 2, 3 получаем префиксную нормальную форму.
В качестве примера рассмотрим следующее выражение:
Шаг1: 
Шаг2: 
Шаг 3: нет необходимости.
Шаг 4: используем выражение 1 по переменной z –
Теперь применяем выражение 1 по переменной w –
4.2.2.2 Скалемовская нормальная форма
Дальнейшее преобразование предполагает полное исключение из формулы кванторов. При этом необходимо сохранить семантику. Это достигается за счет введения скалемовских функций. Для описания этой функции рассмотрим следующий пример: ("x)($y)подсистема(x,y), для каждого x существует y такой, что x его подсистема.
Это означает, что если выделить конкретное x, то для этого x существует y, удовлетворяющее функции подсистема(x, y). Иными словами, y зависит от x, то есть, если задано x, то и существует соответствующее ему y. Отсюда следует, что y можно заменить на функцию f(x), которая задает отношение между x и y. Поскольку f(x) возникло из-за того, что переменная y квантифицирована $, при подстановке функции на место y, квантор $ уже не требуется. Таким образом, исходную логическую формулу можно переписать: ("x) подсистема(x, f(x).
Такая функция называется скалемовской.
Приоритетность действия кванторов, имеющихся в префиксной форме, определяется слева направо. Например: ("x)($y)("z)F(x, y, z) Þ ("x)("z)F(x, f(x), z). А для случая: ("x)("z)($y)F(x, y, z) Þ ("x)("z)F(x, f(x, y), z).
Таким образом, переменной, которая в логической формуле влияет на связанную квантором существования переменную, является любая переменная с квантором общности, которая стоит левее переменной из квантора существования. Если переменная связанная квантором существования является крайней слева, такую формулу можно заменить функцией без аргументов (константой):
($x)("y)подсистема(x, y) =подсистема.
Если проделать эту операцию для примера, получим:
В случае, когда в одной логической формуле имеется более двух связанных квантором существования переменных, то сколемовская функция также будет распадаться на различные функции.
("x)($y)("z)($w)F(x,y,z, w) = ("x)("z)F(x, f(x), z, g(x, z)).
Если подобным образом исключить связанные квантором существования переменные, то любые другие переменные будут связаны только квантором общности и не надо пояснять, что преременные связаны этим квантором. Следовательно, квантор общности можно исключить. Для примера получим:
Такое представление и есть сколемовская нормальная форма.
Теперь можем определить алгоритм получения сколемовской формы:
1. Составить список L переменных, связанных квантором общности. Сначала список L пуст.
2. Пусть Ci – рассматриваемое предложение, j – номер использующейся сколемовской функции Sij. Положим j = 1.
3. Удалить кванторы, начиная с самого левого и применяя в зависимости от необходимости правила а или б.
а. Если рассматривается квантор "x, то удалить его и добавить x к списку L.
б. Если рассматривается квантор $x, то удалить его и заменить x во всем предложении Ci термом Sij(x1, …, xk), где x1, …, xk переменные, находящиеся в этот момент в списке L. Увеличить j на 1.
Следующим шагом является переход к конъюнктивной нормальной форме, а затем к клаузальной форме, то есть форме предложений.
Приведение к конъюнктивной нормальной форме осуществляется заменой пока это возможно (AÙB)ÚC на (AÚC)Ù(BÚC). В результате получим выражения вида A1Ù … ÙAn, где Ai имеет вид (
, причем 
есть терм или атомарный предикат или атомарная формула или их отрицание. Целесообразно осуществить и минимизацию по следующим правилам:
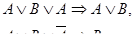
Наконец, исключаем связку Ù, заменяя AÙB на две формулы A, B. В результате многократной замены получим множество формул, каждая из которых является предложением. Это и есть клаузальная нормальная форма.
4.2.2.3 Предложения Хорна
Все клаузальные формулы (предложения) представляют собой несколько предикатов, то есть:
Эти формулы в зависимости от k, l классифицируются по нескольким типам.
(1) Тип 1: k = 0, l = 1.
Предложение представляет собой единичный предикат, и оно может быть записано как ®F(t1, t2, …, tm), где t1, t2, …, tm – термы. В случае когда все термы представляют собой константы, они описывают факты, которые соответствуют данным из БД. Если термы содержат переменные, то они задают общезначимые представления, высказываемые для группы фактов. Например, таким представлением является:
® текучесть(x): все течет, все изменяется.
(2) Тип 2: k³1, l = 0.
Этот тип можно записать в виде:
F1ÙF2Ù…ÙFk®.
Обычно используется для описания вопроса. Причина, по которой данный тип предложения представляется вопросом, является то, что ответ на вопрос реализуется в виде процедуры доказательства, однако для этого доказательства используется метод опровержения, при котором создается отрицание вопроса и доказывается, что отрицание не выполняется.
(3) Тип: k³1, l=1.
Этот тип соответствует записи в форме «Если ___, то ____.».
F1ÙF2Ù…ÙFk®G1.
(4) Тип: k=0, l>1.
Этот тип имеет вид:
® G1ÚG2Ú…ÚGl
и используется при представлении информации, содержащей нечеткость. Обычно нечеткость возникает при неполноте информации. В этой формуле появляется неполнота информации в том смысле, что из нее нельзя определить, какой из предикатов G1, …, Gl является истиной.
(5) Тип: k³1, l>1.
Это наиболее общий тип.
В системе предложений Хорна среди всех перечисленных типов предложений допустимы типы предложений 1, 2, 3, а 4, 5 запрещены.
4.2.3Формализация процесса доказательств
Доказательство демонстрирует, что некоторая ППФ является теоремой на заданном множестве аксиом S (то есть результатом логического вывода из аксиом).
Положим, что S есть множество из n ППФ, а именно, A1, A2, …, An, и пусть ППФ, для которой требуется вычислить является ли она теоремой, есть B. В таких случаях можно сказать, что доказательство показывает истинность ППФ вида:
(A1Ù…ÙAn®B) (1)
при любой его интерпретации. Можно сказать по другому: это определение эквивалентно тому, что отрицание формулы:
(2)
не выполняется (ложно) при любой интерпретации.
Поскольку эта формула является ППФ, то ее можно преобразовать к клаузальной форме, используя для этого приведенный выше алгоритм. Пусть преобразованная ППФ есть S.
Основная идея метода, называемого методом резолюции, состоит:
1. В проверке содержит или не содержит S пустое предложение.
2. В проверке выводится или не выводится пустое предложение из S, если пустое предложение в S отсутствует.
Любое предложение Ci, из которого образуется S, является совокупностью атомарных предикатов или их отрицаний (предикат и его отрицание называются литералами), соединенных символами дизъюнкции, вида:
Сама же S является конъюнктивной формой, то есть имеет вид:
Следовательно, условием истинности S является условие истинности всех Ci в совокупности.
Условием ложности S является ложность по крайней мере одного Ci. Однако, условием, что Ci будет ложным в какой-нибудь интерпретации, является то, что множество 
будет пустым. Это легко показать. Положим, что это не так, тогда среди всех возможных интерпретаций имеется такая, что какой-нибудь из литералов этого множества или все они будут истиной и тогда Ci не будет ложью. Следовательно, если S содержит пустые предложения, формула (2) является ложью, а это показывает, что B выводится из группы предикатов A1, …, An, то есть из S.
4.2.3.1 Метод резолюций для логики высказываний
Предикат, который не содержит переменных, совпадает с высказыванием. Для упрощения рассмотрим сначала резолюцию для высказываний.
Предположим, что в множестве предложений есть дополнительные литералы (которые отличаются только символами отрицания L и 
) вида:
Исключим из этих двух предложений дополнительные литералы и представим оставшуюся часть в дизъюнктивной форме (такое представление называется резольвентой):
После проведения этой операции легко видеть, что C является логическим заключением Ci и Cj. Следовательно, добавление C к множеству S не влияет на вывод об истинности или ложности S. Если выполняется Ci = L, 
то C пусто. То что C является логическим заключением из S и C пусто, указывает на ложность исходной логической формулы.
Приведем простой пример такого доказательства:
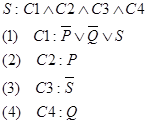
Получим доказательство принципом резолюции:
- пустое предложение.
Такой вывод теорем из аксиоматической системы носит название дедукции. Алгоритм дедуктивного вывода удобно представлять с помощью древовидной структуры:
