Поиск по дереву с включением и исключением
6.1. Цель работы:
- исследовать и изучить методы поиска элемента в дереве по заданному ключу со вставкой (включением) и удалением (исключением);
- овладеть умениями и навыками написания на С++ программ поиска по дереву с включением и исключением.
Порядок выполнения работы
- ознакомиться с краткой теорией и примерами решения задач, относящихся к поиску по дереву с включением и исключением;
- ответить на контрольные вопросы и получить оценку по знанию теории;
- получить задание на выполнение конкретного варианта лабораторной работы и выполнить его;
- написать и отладить программу решения задачи на языке С++;
- составить отчет по лабораторной работе и защитить его у преподавателя.
Содержание отчета по ЛР
- наименование ЛР и ее цель;
- задание на ЛР согласно варианту;
- листинг приложения, обеспечивающей успешное решение студентом полученного варианта задачи;
- результаты работы программы.
Краткая теория
В лабораторной работе № 3 были рассмотрены основные понятия, касающиеся сбалансированных бинарных деревьев, и представлены алгоритмы создания и возможных обходов бинарных деревьев. В данной работе будут рассмотрены случаи, когда дерево уже создано и необходимо осуществить поиск элемента по ключу в уже имеющемся бинарном дереве. На практике часто может возникать необходимость вначале осуществить поиск элемента в структуре, а затем, в случае, если элемент найден, либо информировать пользователя об этом, либо удалить его. В случае, если элемент не найден, пользователя необходимо либо об этом проинформировать, либо вставить в структуру элемент с ненайденным ключом.
Поиск по бинарному дереву.
Назначение его в том, чтобы по заданному ключу осуществить поиск узла дерева. Также для вставки элемента в дерево сначала нужно осуществить поиск в дереве по заданному ключу. Если такой ключ имеется, то программа завершается, если нет, то происходит вставка. Длительность операции поиска (число узлов, которые надо перебрать для этой цели) зависит от структуры дерева. Действительно, дерево может быть вырождено в однонаправленный список (иметь единственную ветвь) - такое дерево может возникнуть, если элементы поступали в дерево в порядке возрастания (убывания) их ключей, например:
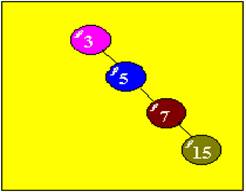
В этом случае время поиска будет такое же, как и однонаправленном списке, т.е. в среднем придется перебрать n /2 элементов.
Наибольший эффект использования дерева достигается в том случае, когда дерево "сбалансировано". В этом случае для поиска придется перебрать не более log2n.
Включение элемента в дерево
Для включения новой записи в дерево, прежде всего, нужно найти тот узел, к которому можно "подвесить" (присоединить) новый элемент. Алгоритм поиска нужного узла тот же самый, что и при поиске узла с заданным ключом. Этот узел будет найден в тот момент, когда в качестве очередной ссылки, определяющий ветвь дерева, в которое надо продолжить поиск, окажется ссылка NIL.
Однако непосредственно использовать процедуру поиска нельзя, потому что по окончанию вычисления ее значение не фиксирует тот узел, из которого была выбрана ссылка NIL. Модифицируем описание процедуры поиска так, чтобы в качестве ее побочного эффекта фиксировалась ссылка на узел, в котором был найден заданный ключ (в случае успешного поиска), или ссылка на узел, после обработки которого, поиск прекращен (в случае неуспешного поиска).
Исключение элемента из дерева
Удаление узла дерева не должно нарушать упорядоченность дерева. При удалении возможны 3 расположения узлов:
1) найденный узел является листом - он просто удаляется;
2) найденный узел имеет только сына - в этом случае сын перемещается на место удаленного отца;
3) у удаляемого отца два сына - в этом случае основная трудность состоит в удалении отца, поскольку в удаляемую вершину входит одна стрелка, а выходит две. В этом случае нужно найти подходящее звено поддерева, которое должно занять место удаляемого без нарушения упорядоченности дерева. Данным звеном может быть либо предшественник удаляемого узла, либо его приемник.
Предшественник - это самый правый элемент левого поддерева (для достижения этого элемента необходимо перейти в следующий узел по левой ветви, а затем двигаться только по правой ветви этого узла до тех пор, пока очередная ссылка не будет равна nil).
Приемник - это самый левый элемент правого поддерева (для достижения этого элемента необходимо перейти в следующий узел по правой ветви, а затем двигаться только по левой ветви этого узла до тех пор, пока очередная ссылка не будет равна nil).
Очевидно, что такие подходящие звенья могут иметь не более одной ветви.
На изображенном ниже рисунке проиллюстрированы возможные удаляемые из дерева узлы при трех возможных вариантах (лист (ключ 1), один сын (ключ 6), два сына (ключ 12)).
Предшественником удаляемого узла (12) является самый правый узел левого поддерева (11). Преемником узла (12) - самый левый узел правого поддерева (13).

Функция поиска по бинарному дереву
Переменной search будет присваиваться указатель на найденное звено:
p = tree
whlie p <> nil do
if key = k(p) then
search = p
return
endif
if key < k(p) then
p = left(p)
else
p = right(p)
endif
endwhile
search = nil
return