Преобразование чертежа способом замены
плоскостей проекций.
Приведение прямых линий и плоских фигур в частные положения относительно плоскостей проекций в ходе решения задач нередко приводит к значительному упрощению решения.
Способ замены плоскостей проекций заключается в том, что одна из основных плоскостей проекций (π1 , π2) заменяется дополнительной плоскостью проекций, подходящим образом расположенной относительно оригинала, но перпендикулярно остающейся плоскости проекций.
Преобразование прямой
Используя способ замены плоскостей проекции, прямую общего положения АВ можно преобразовать в прямую уровня или прямую проецирующую (рис. 18).
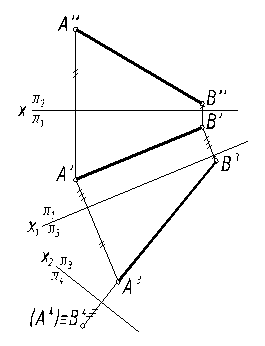Если выбрать дополнительную плоскость проекций π3 параллельно прямой АВ, тогда прямая станет прямой уровня в системе π1/π3, что позволит найти натуральную величину отрезка прямой.
После этого преобразования перпендикулярно к прямой АВ можно построить дополнительную плоскость
|
Преобразование плоскости
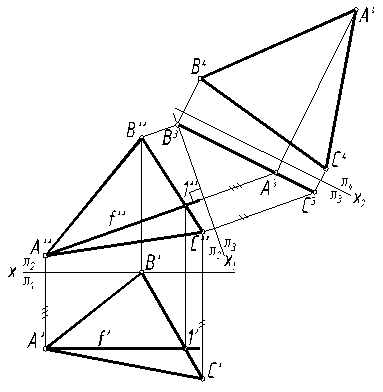
Плоскость общего положения α(ABC) можно преобразовать в проецирующую, если выбрать дополнительную плоскость π3 перпендикулярно к любой прямой, принадлежащей плоскости α. В качестве такой прямой выбирают линию уровня плоскости (фронталь или горизонталь). Пусть π3 ^ f (x1 ^ f”), следовательно, и вся плоскость α будет перпендикулярной к π3 (рис. 19).
Если выбрать дополнительную плоскость π4 параллельно проеци-рующей плоскости α, то можно получить натуральный вид плоской фигуры, лежащей в плоскости α.
|
 |
4.2. Последовательность выполнения
графической части работы
Задача №1
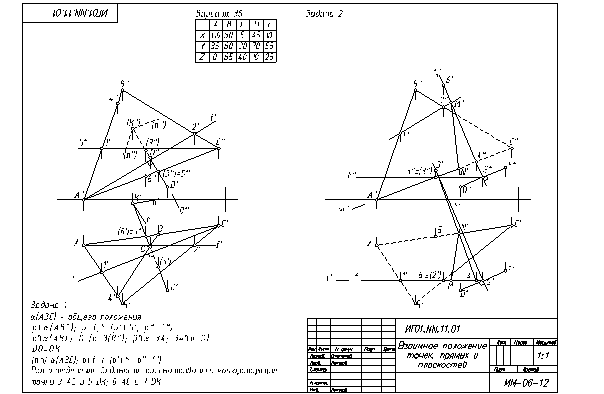
По заданным координатам точек А, В, С и D строятся проекции плоскости α(ABC) и точки D (рис. 20).
Точка K находится на прямой, проведенной из точки D перпендикулярно к плоскости α.
Анализ данных показывает, что плоскость α(ABC) - общего положения, следовательно, для построения этого перпендикуляра необходимо преобразовать чертеж так, чтобы плоскость α стала проецирующей к дополнительной плоскости проекций π3.
Для преобразования используем фронталь плоскости α (прямая A1) π3 ^ A1 (x1 ^ A”1”).
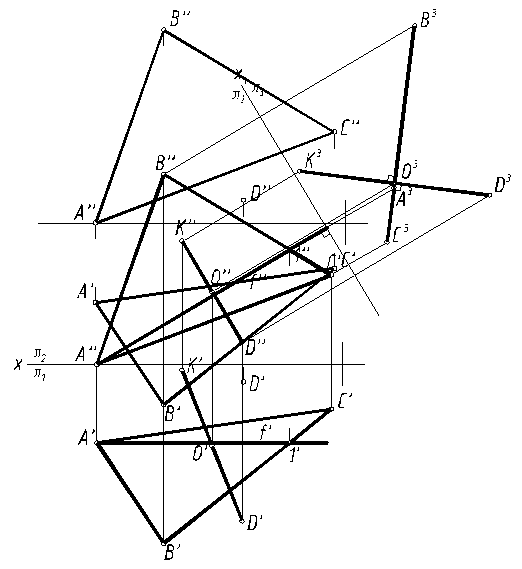
На дополнительной плоскости проекций π3 выполняем построения проекций перпендикуляра к плоскости α, проходящего через точку D. Точка пересечения перпендикуляра с плоскостью (точка O) – середина отрезка DK. Затем выполняется построение исходных проекций отрезка DK и точки O. (Прямая DK является прямой уровня в системе π2/π3, следовательно, D”K” должна быть параллельна оси проекций x1 ) (рис.21).
В точке K построена плоскость, параллельная плоскости α, заданная двумя пересекающимися прямыми m и n, причем m || АС, n || АВ.
В завершении задачи определена видимость отрезка DK относительно плоскости α и выполнена обводка.
При определении видимости рассматривались конкурирующие точки отрезка DK и одной из скрещивающихся с ним сторон треугольника ABC – точки 2ÎAC и 3ÎDK; точки 4ÎAC и 5ÎDK (рис. 22).
| |||
|
|
Задача №2
По заданным координатам точек А, В, С, D и Е строятся проекции плоскости α(ABC) и отрезка DE (рис. 23).
Геометрическим местом точек, равноудаленных от концов отрезка DE, будет плоскость β, проходящая перпендикулярно отрезку через его середину.
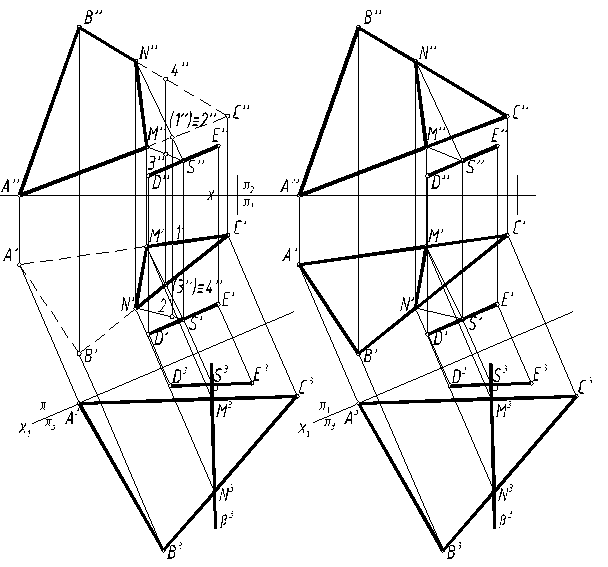
Решение задачи сводится к построению линии пересечения плоскостей α(ABC) и β.
Для построения плоскости перпендикулярной к отрезку DE необходимо преобразовать чертеж таким образам, чтобы отрезок стал параллелен дополнительной плоскости проекций π3 . Выбираем новую ось проекций x1 параллельно любой проекции отрезка DE (например, горизонтальной D′E′).
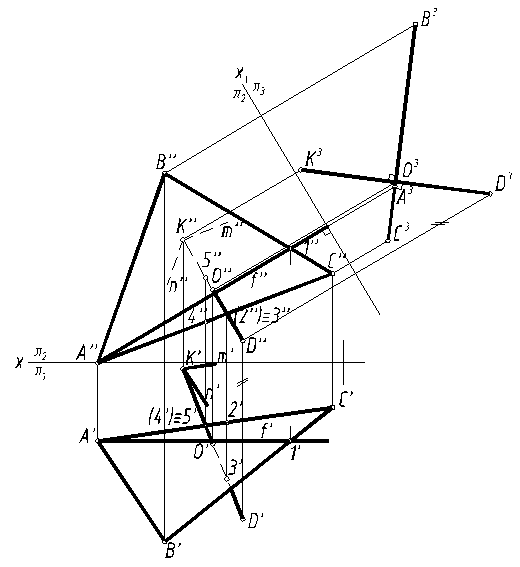
После преобразования чертежа через середину проекции D3K3 можно построить плоскость β(β3) перпендикулярно к отрезку.
Линией пересечения плоскости α(ABC) с плоскостью β будет прямая, проходящая через точки M и N, принадлежащие прямым AC и BC.
По дополнительной проекции (M3N3) выполняется построение исходных (M’N’ и M”N”) проекций линии пересечения (рис. 24).
Проекции плоскости β на плоскостях проекций π1 и π2 можно считать заданными прямой MN и точкой S.
В заключение определена видимость треугольника АВС относительно плоскости β и произведена обводка чертежа.
При определении видимости рассматривались конкурирующие точки скрещивающихся прямых, принадлежащих плоскостям α и β – точки 1ÎAC и 2ÎSN; точки 3ÎSM и 4ÎBC (рис. 25).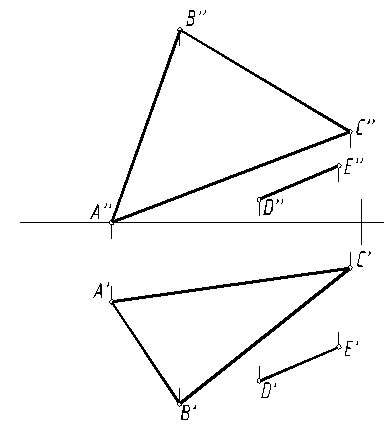 
|
| |||
|
 |
5. Оформление домашней графической работы
Графическая работа выполняется на ватмане формата A3 (420x297) карандашом в масштабе 1:1.
Допускается выполнение работы на двух листах формата А3. В этом случае основная надпись на втором листе должна быть выполнена по форме 2.
Линии чертежа должны соответствовать ГОСТ 2.303-68. Рекомендуемая толщина сплошной основной линии 0,8...1мм.
Все надписи на чертеже и размерные числа выполняются стандартным шрифтом (ГОСТ 2.304-81). Рекомендуемая высота букв и цифр 3,5 или 5мм.
Алгоритм решения задач в краткой форме записывается рядом с графическим решением. Объяснение решения строится на операциях с объектами в пространстве, и только в самых необходимых случаях поясняются графические построения.
Допускается знаковая запись последовательности решения: в виде отношений пересечения (∩), параллельности (||), перпендикулярность (^), результата операции (=) и других, но не в ущерб ясности изложения.
Допускается изменение обозначений точек и прямых, кроме А, В, С, D, Е. Уровень подробности объяснения выбирается автором работы.
В правом нижнем углу рабочего поля чертежа размещается «основная надпись» (ГОСТ 2.104-68, форма 1), в верхней графе которой указывается обозначение чертежа: ИГ01.NN.11.01,
где ИГ - буквенный индекс, обозначающий наименование
дисциплины - «Инженерная графика»;
01 - номер семестра;
NN - вариант, соответствующий номеру студента в журнале
группы;
01 - номер чертежа.
Структура обозначения сформирована по образцу обозначения конструкторских документов (ГОСТ 2.201-80), поэтому индекс ИГ не отделяется точкой от номера семестра, и в конце обозначения отсутствует точка.
Основным условием успешного выполнения и оформления чертежа является точность графических операций, поэтому на нем должны присутствовать промежуточные построения, выполняемые сплошными тонкими линиями в ходе решения задач.
6. Литература
1. Гордон В.О., Семенцов-Огиевский М.А.
Курс начертательной геометрии: Учебник. -М.: Наука, 1988.
2. Иванов Г.С. Начертательная геометрия: Учебник.
-М.: Машиностроение, 1995.
3. ЕСКД: ГОСТ 2.301-69... 2.304-81.
Приложение 1.
Приложение 2.
Приложение 3.
Вопросы для подготовки
к защите домашней графической работы
1. Какие геометрические элементы включает в себя аппарат прямоугольного проецирования?
2. В чем состоят свойства прямоугольного проецирования?
3. Как образуется комплексный чертеж?
4. При каком положении относительно плоскостей проекций прямая называется прямой общего положения?
5. В чем состоит отличительная особенность прямоугольных проекций прямых особого (частного) положения?
6. Что представляет собой след прямой линии на плоскости проекций?
7. Какая координата равна нулю:
а) для фронтального следа прямой,
б) для горизонтального следа прямой?
8. Как определить величину и углы наклона отрезка прямой общего положения по его комплексному чертежу?
9. Как могут располагаться в пространстве две различные прямые?
10. В чем состоит особенность прямоугольных проекций:
а) пересекающихся прямых,
б) параллельных прямых,
в) скрещивающихся прямых?
11. Какие точки являются конкурирующими?
12. Как определится видимость пересекающихся прямой с плоскостью, двух плоскостей с помощью конкурирующих точек?
13. В каком случае плоский прямой угол проецируется в виде прямого угла?
14. Какими элементами пространства можно задать плоскость?
15. Какая плоскость называется плоскостью общего положения?
16. Что характерно для комплексного чертежа плоскости частного положения?
17. Как изображается на чертеже фронтально проецирующая (горизонтально проецирующая) плоскость, проведенная через прямую общего положения?
18. Какие плоскости можно провести через фронтально проецирующую (горизонтально проецирующую), фронтальную (горизонтальную) прямую?
19. Как на чертеже построить проекции точки, принадлежащей плоскости?
20. Как построить прямую, принадлежащую плоскости?
21. Какие линии плоскости называются линиями уровня, в чем состоят особенности их изображений?
22. Как относительно друг друга могут быть расположены в пространстве прямая линия и плоскость, две плоскости?
23. Как найти точку пересечения прямой
а) с плоскостью частного положения,
б) с плоскостью общего положения?
24. Как найти линию пересечения плоскости частного положения с плоскостью общего положения, двух плоскостей общего положения?
25. Как реализуется на комплексном чертеже признак параллельности прямой и плоскости, двух плоскостей?
26. Как расположена прямая относительно плоскостей проекций, если она перпендикулярна
а) горизонтально проецирующей плоскости,
б) фронтально проецирующей плоскости,
в) плоскости общего положения?
27. Как направлены проекции перпендикуляра, проведенного к плоскости общего положения?
28. В чем заключается способ преобразования чертежа методом перемены плоскостей проекции?
29. Как найти длину отрезка прямой линии и углы этой прямой с плоскостями π1 и π2 при помощи метода замены плоскостей проекции?
30. Сколько требуется выполнить замен плоскостей проекций, чтобы прямая общего положения стала проецирующей?
31. Как выбрать дополнительную плоскость проекций π3 , чтобы заданную плоскость общего положения преобразовать в проецирующую?
32. Сколько и в какой последовательности надо сделать замен плоскостей проекций, чтобы получить натуральный вид плоской фигуры?
Содержание
1. Предисловие……………………………………………………………. 3
2. Исходные данные…………………………………….………………… 4
3. Вариант 1……………………………………………………………….. 4
3.1 Краткие теоретические обоснования решения задач…………... 4
Точка и прямая. Взаимное положение прямых………………. 4
Прямая и точка в плоскости.
Горизонтали и фронтали плоскости…………………………... 5
Параллельные прямая и плоскость.
Параллельные плоскости………………………………………. 6
Пересечение прямой с плоскостью………………………….… 7
Пересечение двух плоскостей…………………………………. 8
Перпендикулярные прямые…………..………………………... 9
Перпендикулярные прямые и плоскость……………..……….. 9
Перпендикулярные плоскости………………..………………... 10
3.2. Последовательность выполнения графической части работы..…. 11
Задача №1…………………………………………………….…. 11
Задача №2…………………………………………………….… 13
4. Вариант 2……………………………………………………………….. 15
4.1 Краткие теоретические обоснования решения задач…………... 15
Преобразование чертежа способом замены
плоскостей проекций……………………………………………. 15
Преобразование прямой…………………………….………. 15
Преобразование плоскости……………………………….… 16
4.2. Последовательность выполнения графической части работы..…. 17
Задача №1…………………………………………..……………. 17
Задача №2………………………………………………………… 19
5. Оформление домашней графической работы………………………… 22
6. Литература………………………………………………………………. 23
Приложение 1……………………………………………………………… 24
Приложение 2……………………………………………………………… 25
Приложение 3……………………………………………………………… 26
Приложение 0.