Краткие теоретические обоснования решения задач

Федеральное агентство по образованию

РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
НЕФТИ И ГАЗА им. И.М. ГУБКИНА

А.В. Бочарова, Т.П. Коротаева

ИНЖЕНЕРНАЯ ГРАФИКА

Точка, прямая плоскость на комплексном чертеже

Методические указания
к выполнению домашней графической работы
для студентов первого курса всех специальностей
факультетов ИМ, РНиГМ, ПСиЭСТТ, ХТиЭ и АиВТ

 

Москва 2007

УДК 55:744

Методические указания к выполнению домашней графической работы по курсу «Инженерная графика»/ А.В. Бочарова, Т.П. Коротаева,
- М.: РГУ нефти и газа им. И.М. Губкина, 2007. – 26с.

Даны основные теоретические обоснования и приведен порядок выполнения работы по курсу «Инженерная графика»

© Российский государственный университет нефти и газа им. И.М.Губкина, 2007

1. Предисловие

Тема «Взаимное положение точек, прямых и плоскостей» входит в число основных тем теории построения чертежа. Здесь рассматривается отображение на комплексном чертеже принадлежности точки прямой и плоскости, принадлежности прямой плоскости, взаимного положения прямых (пересекающихся, параллельных, перпендикулярных, скрещивающихся), взаимного положения прямой и плоскости, взаимного положения плоскостей (параллельность, пересечение, перпендикулярность). Построения на чертежах строго соответствуют отношениям точек, прямых и плоскостей, установленным в курсе стереометрии признаками принадлежности, параллельности и перпендикулярности.

Выполнение предусмотренной учебной программой курса домашней графической работы на эту тему способствует развитию пространственного мышления учащегося и готовит его к решению последующих задач. Работа предназначена также для проверки усвоения материала по теоретическим основам построения чертежа, умения применять эти знания в решении задач, формулировать алгоритмы решения; нацелена на отработку навыков выполнения чертежей с применением чертежных инструментов в соответствии со стандартами ЕСКД.

В предлагаемом пособии предусмотрены два варианта решения задач:
- без использования методов преобразования чертежа;
- с применением метода замены плоскостей проекций.

Учащийся обязательно знакомиться с методикой выполнения задач по каждому варианту, изложенному в пособии, а затем сам выбирает вариант графического решения.

Домашняя графическая работа - часть предусмотренной учебным планом самостоятельной работы студента над курсом (объемом около 10 часов). Она выполняется в период со 2-ой по 6-ую неделю и подлежит защите в виде собеседования с преподавателем в качестве рубежного контроля знаний.

Вопросы для подготовки к защите помещены в приложении 3.

2. Исходные данные

Исходными данными для выполнения работы являются условия задач и координаты пяти точек А, В, С, D, Е в соответствии с индивидуальным заданием.

Задача №1

Через точку К, симметричную точке D относительно плоскости α(ABC), построить плоскость, параллельную плоскости α.

Задача №2

На плоскости α(ABC) построить множество точек, равноудаленных от концов отрезка DE.

A	B	C	D	E
X	Y	Z	X	Y	Z	X	Y	Z	X	Y	Z	X	Y	Z
110	35	0	80	80	85	5	20	40	45	70	10	10	55	25

3. Вариант 1

Краткие теоретические обоснования решения задач

Точка и прямая. Взаимное положение прямых

Принадлежность точки прямой линии на комплексном чертеже отражается принадлежностью проекций точки одноименным проекциям прямой. Поэтому пересекающиеся прямые, имеющие общую точку М, на чертеже изображаются пересекающимися проекциями, точки пересечения которых (М″, М′) лежат на одной линии связи (рис. 1а).

б.

а.

Рис. 1.

Если прямые скрещивающиеся, то точки пересечения их проекций не лежат на одной линии связи и представляют собой проекции пары «конкурирующих» точек (рис. 1б).

Следует обратить особое внимание на то, что «конкурирующими» называют точки, лежащие на одной проецирующей прямой. Та из них, которая расположена дальше от плоскости проекций, считается видимой.

б.

Рис. 1.

а.

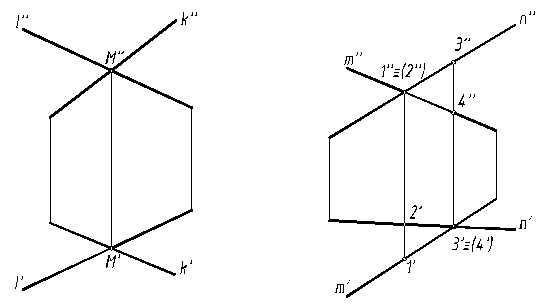
Это точка 1 на фронтальной проекции и точка 3 на горизонтальной (рис.1б). Проекции невидимых точек условились заключать в скобки.

Параллельные прямые изображаются параллельными одноименными проекциями, то есть должны быть параллельны друг другу фронтальные проекции прямых и также взаимно параллельны горизонтальные проекции.

Прямая и точка в плоскости.
Горизонтали и фронтали плоскости

Принадлежность точки плоскости согласно «признаку принадлежности» очевидна, если точка принадлежит прямой, лежащей в плоскости. Прямая, в свою очередь, принадлежит плоскости, если две ее точки находятся в плоскости.

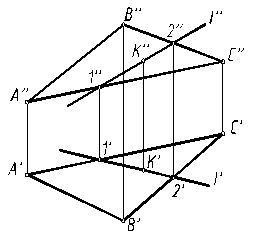Пусть плоскость задана треугольником ABC (рис. 2).

Прямая l лежит в плоскости ABC, так как две ее точки (1 и 2) принадлежат плоскости. И точка K лежит в плоскости, так как находится на прямой l.

Рис. 2.

Для решения некоторых задач требуется в плоскости выбирать прямые, параллельные плоскостям проекций π₁ и π₂. Такие прямые часто называют «линиями уровня» плоскости.

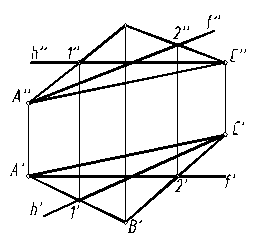Прямая h, параллельная π₁ и лежащая в плоскости, называется горизонталью плоскости ABC (рис. 3).

Рис. 3.

Прямая f, параллельная π₂ и лежащая в плоскости, называется фронталью плоскости ABC.

В любой плоскости бесчисленное множество как горизонталей, так и фронталей. Выбор необходимой линии уровни диктуется в какой-то мере условием задачи. Например, горизонталь плоскости ABC удобнее провести через точку C, а фронталь - через точку А, что сокращает графические операции.

Рис. 6.

Рис. 5.

Рис. 3.

Параллельные прямая и плоскость.
Параллельные плоскости

Известно, что прямая параллельна плоскости, если она параллельна прямой, лежащей в плоскости. Например, прямая m параллельна прямой l, лежащей в плоскости (рис. 4).

Рис. 4.

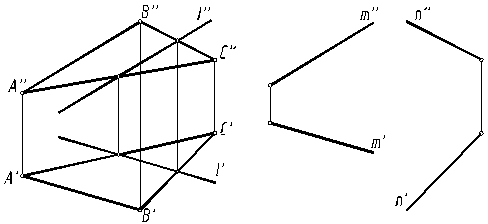
Параллельны плоскость ABC и прямая n, параллельная стороне ВС, и т.д.

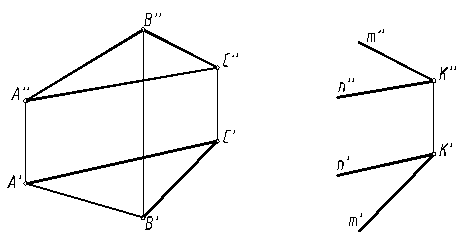Согласно признаку параллельности плоскостей две пересекающиеся прямые одной плоскости должны быть параллельны двум пересекающимся прямым другой плоскости, тогда эти плоскости будут параллельны.

Рис. 5.

При построении плоскости, параллельной плоскости ABC, через некоторую точку К, должны быть проведены проекции прямых m и n, параллельные проекциям выбранных в плоскости ABC двух пересекающихся прямых, например, ВС и АС, и обязательно обозначены (m", m', n", n'). В противном случае решение неопределенно (см. рис. 5).

Пересечение прямой с плоскостью

Если прямая и плоскость не параллельны, то они пересекаются в точке, которая принадлежит как прямой, так и плоскости.

Определение точки пересечения прямой l с плоскостью ABC в общем случае выполняется в такой последовательности (рис. 6):

– через прямую проводят вспомогательную проецирующую плоскость, например, α ^ π₂; ее след α" совпадает с фронтальной проекцией прямой;

– находят линию MN пересечения плоскостей α и ABC;

– фиксируют точку O пересечения прямой l и прямой MN (в данном варианте сначала определяется проекция O').

Рис. 6

Видимость прямой l по отношению к плоскости ABC определена с помощью пар конкурирующих точек F и G, M и P.

Рис. 6.

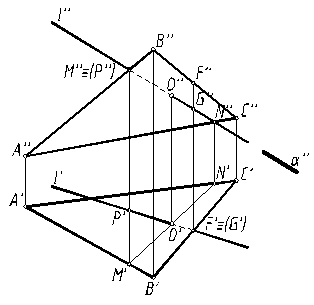Следует заметить, что видимость элементов чертежа на горизонтальной проекции («кон-курирующие» точки F и G) и фронтальной («конкурирующие» точки М и P) определяется индивидуально. Для горизонталь-ной проекции решается вопрос, какая из точек выше, т.е. координата Z больше, та и будет видимой. Это точка F принадлежащая стороне ВС. А для фронтальной проекции – какая из точек ближе (координата Y больше), это точка М, принадлежащая стороне АВ.

Пересечение двух плоскостей

Имеется несколько способов построения линии пересечения двух плоскостей общего положения.

Например, используются две вспомогательные проецирующие плоскости, каждая из которых позволяет найти одну общую точку заданных плоскостей. В основе метода – простота построения линии пересечения плоскости общего положения с проецирующей.

Можно также взять одну из прямых заданной плоскости и найти ее точку пересечения с другой заданной плоскостью. Решив такую задачу дважды, определяют две точки линии пересечения плоскостей. Выбор прямых произволен и диктуется удобством решения, в частности тем, чтобы искомая точка находилась в пределах чертежа. Этот способ отличается от предыдущего меньшим числом графических построений, а значит, большей точностью решения.

Перпендикулярные прямые

Пересекающиеся и скрещивающиеся прямые в пространстве могут располагаться в частности под прямым углом друг к другу. Если обе прямые – общего положения, то факт их перпендикулярности на чертеже не отражается: проекцией прямого угла будет тупой (острый) угол.

И только в случае, если одна из прямых параллельна плоскости проекций, прямой угол проецируется в натуральную величину на ту плоскость, которой прямая параллельна. Это предложение (теорема) является основополагающим для изображения на чертеже взаимно перпендикулярных прямых: тогда и только тогда прямой угол проецируется в натуральную величину, если хотя бы одна его сторона параллельна плоскости проекций, а следовательно, является или

б.

а.

Рис. 7.

фронталью, или горизонталью.

 

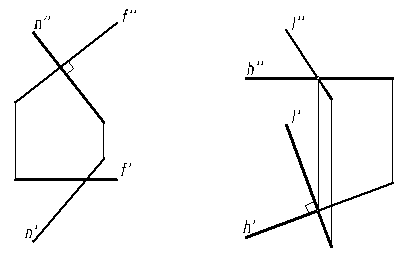
На рис.7,а изображены взаимно перпендикулярные скрещивающиеся прямые на рис.7,б – пересекающиеся под прямым углом.

Перпендикулярные прямая и плоскость

Согласно признаку перпендикулярности в данной плоскости должны быть две пересекающиеся прямые, перпендикулярно которым следует направить перпендикуляр к этой плоскости.

Рис. 8.

Известно, что перпендикуляр к плоскости перпендикулярен любой прямой этой плоскости. Но на плоскость проекций, как известно, прямой угол проецируется только тогда, когда хотя бы одна его сторона параллельна плоскости проекций. Поэтому в качестве двух пересекающихся прямых плоскости следует выбрать любые горизонталь и фронталь этой плоскости. Тогда фронтальная проекция перпендикуляра должна быть направлена перпендикулярно фронтальной проекции фронтали плоскости, а горизонтальная пройдет перпендикулярно горизонтальной проекции горизонтали. Построение двух проекций перпендикуляра определяет только его направление в пространстве. В общем случае перпендикуляр и линии уровня плоскости – скрещивающиеся прямые, и точек их пересечения не существует.

Если требуется найти точку пересечения перпендикуляра с плоскостью, то задача решается по известной методике (см. стр.7.).

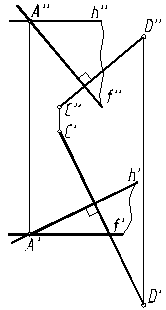
Обратную задачу – построение плоскости, перпендикулярной данной прямой – логично решить заданием плоскости ее линиями уровня, так как направление их проекций известно. Так в точке A построена плоскость α(f∩h) перпендикулярная отрезку CD (рис. 8).

Перпендикулярные плоскости

Известно, что плоскости перпендикулярны, если одна из них проходит через перпендикуляр к другой.

Поэтому, построение плоскости, перпендикулярной данной, предполагает построение перпендикуляра к ней из любой точки, заведомо принадлежащей искомой плоскости.

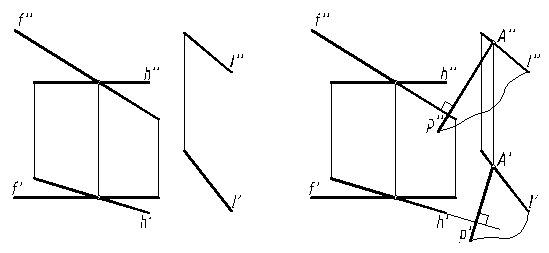Пусть через прямую l требуется построить плоскость, перпендикулярную данной, которая задана своими горизонталью h(h”, h’) и фронталью f(f”, f’) (рис. 9а).

Рис. 9.

а.

б.

Решение сводится к построению в некоторой точке A, принадлежащей прямой l, перпендикуляра p, причем p” ^ f”, p’ ^ f’ (рис.9б).

Если в данной плоскости линии уровня отсутствуют, то их предварительно нужно построить.

3.2. Последовательность выполнения
графической части работы

Задача №1

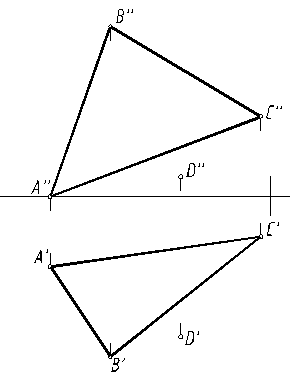
По заданным координатам точек А, В, С и D строятся проекции треугольника ABC (плоскости α) и точки D (рис. 10).

Очевидно, точки D и К, симметричные относительно плоскости α(ABC) располагаются на перпендикуляре к плоскости и на равном расстоянии от нее.

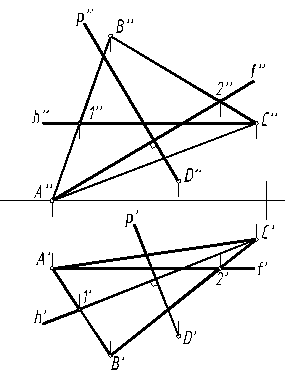
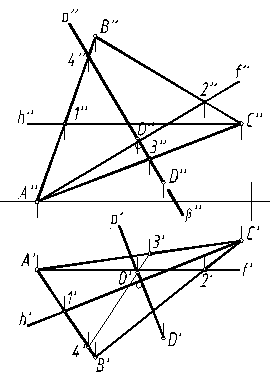
Анализ данных показывает, что плоскость α(ABC) - общего положения, поэтому проекции р", р' перпендикуляра приходится строить, ориентируясь на ее линии уровня f и h: р" ^ f", р’ ^ h’. Построения на чертеже сопровождаются обозначением проекций характерных точек и линий (рис. 11).

Следующим шагом будет построение точки O пересечения перпендикуляра р с плоскостью α(ABC). В качестве вспомогательной плоскости в примере выбрана фронтально проецирующая плоскость β(β″), которая пересекает плоскость α по прямой (34). В пересечении (З'4') и р' определяется O'. Затем проведением линии связи находится O" (рис. 12).

Точка К определяется отложением отрезка OК, равного DO, на продолжении перпендикуляра р. Искомая плоскость в точке К, параллельная плоскости α(ABC), задана двумя пересекающимися прямыми m и n, причем m || АС, n || АВ.

В завершение задачи определена видимость отрезка DK перпендикуляра р относительно плоскости α и выполнена обводка.

Рис. 11.

Рис. 10. .

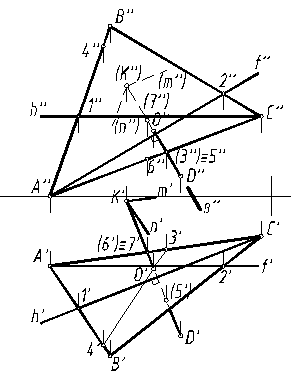
При определении видимости рассматривались конкурирующие точки отрезка DK и одной из скрещивающихся с ним сторон треугольника ABC – точки 3ÎAC и 5ÎDK; точки 6ÎAC и 7ÎDK (рис. 13).

 

 

	Рис. 12.		Рис. 13.

Задача №2

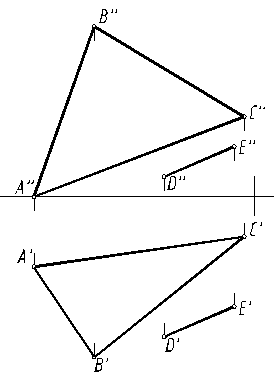
По заданным координатам точек А, В, С, D и Е строятся треугольника ABC (плоскости α) и отрезка DE (рис. 14).

Очевидно все точки, равноудаленные от концов отрезка DE, находятся в плоскости перпендикулярной отрезку и проходящей через его середину.

Условию же задачи будет отвечать линия пересечения с этой плоскостью данной плоскости α(ABC).

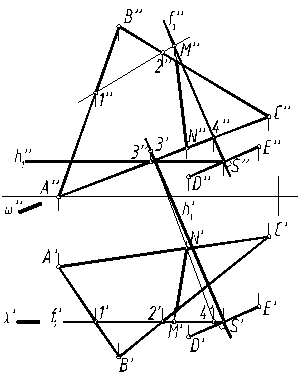
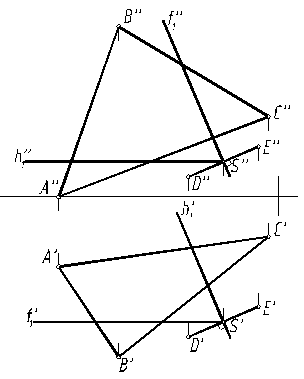
Плоскость γ, перпендикулярная отрезку DE в его середине S (рис.15), задана своими линиями уровня f₁ и h₁.

Две точки М и N линии пересечения плоскостей α и γ определены как точки пересечения прямой f₁ с плоскостью α и прямой АС с плоскостью γ. Для этого использованы вспомогательные плоскости λ и ω. Все построения сопровождаются обозначением проекций характерных точек и линий (рис. 16).

В заключение определена видимость треугольника АВС относительно плоскости γ(f₁ ∩ h₁ ) и произведена обводка чертежа.

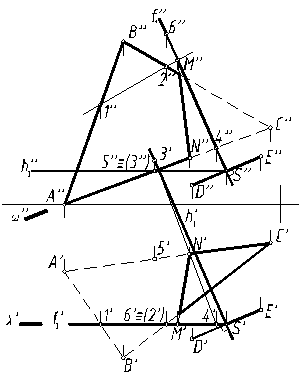
При определении видимости рассматривались конкурирующие точки скрещивающихся прямых, принадлежащих плоскостям α и γ – точки 3Îh₁ и 5ÎAC; точки 2ÎBC и 6Îf₁ (рис. 17).

	Рис. 14. .		Рис. 15. .

	Рис. 16. .		Рис. 17. .

4. Вариант 2