Классификация дифференциальных уравнений с частными производными.

Для решения многих практических задач необходимо рассматривать так называемые линейные или вполне линейные уравнения в частных производных:

Au_xx +Bu_xy +Cu_yy +Du_x +Eu_y +Fu = G (1)

Дифференциальное уравнение с частными производными II порядка с двумя независимыми переменными. A,B,C,D,E.F.G – функции от независимых переменных х и у, имеющие непрерывные частные производные.

Уравнение (1) всегда может быть приведено к одному из трёх стандартных канонических форм:

-- если B² -4AC < 0, то уравнение (1) - эллиптическое;

-- если B² -4AC = 0, то уравнение (1) - параболическое;

-- если B² -4AC > 0, то уравнение (1) – гиперболическое.

К уравнениям с частными производными приводят задачи газодинамики, теплопроводности, процессов переноса в газах, квантовой механики и др.

Полная постановка математической задачи содержит дифференциальное уравнение, а также дополнительные условия, позволяющие выделить единственное решение семейства интегральных поверхностей.

Дополнительные условия называются начальными, если они определяют искомую функцию и её производные в начальный момент времени.

Условия, относящиеся к фиксированным значениям координат, называются краевыми или граничными.

- Граничные условия I рода определяют значения функции на границе области её изменения;

- Граничные условия II рода определяют значения градиента функции на границе области её изменения;

- Граничные условия III рода определяют зависимость функции и её градиента на границе области изменения функции, т.е. в граничных точках пространства записывается дифференциальное уравнение.

Решение дифференциального уравнения с частными производными при заданных начальных условиях называется нестационарной краевой задачей.

Решение дифференциального уравнения с частными производными при заданных граничных условиях называется стационарной краевой задачей.

Пример 1. Исследования стационарных процессов различной физической природы (колебания, теплопроводность, фильтрация и др.) приводят к уравнению эллиптического типа (уравнение Пуассона: ;

Уравнение Лапласа: ).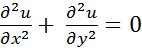

Решение ищется в некоторой области G, на границе этой области Г могут быть заданы краевые условия:

-- первого рода -- u(x;y)_Г = φ(x;y);

-- второго рода -- |_г = φ₁(x;y);

-- третьего рода -- + α₁u = φ₂(x;y); n – нормаль к линии Г.

Пример 2. Примером параболического уравнения может служить уравнение теплопроводности однородного стержня, которое имеет вид:

а² – const.

В начальный момент времени t = t₀ для внутренних точек стержня задаётся начальное распределение температуры: u(x;t₀) = φ(x), φ(x) – известная функция. Начальное условие не обеспечивает однозначности решения, т.к. распределение температуры u(x;t) в стержне для последующих моментов времени t > t₀ существенно зависит от того, в каком состоянии находится концы стержня: х=0 и х=l.

Тогда краевые условия запишутся так:

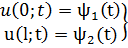ψ₁(t), ψ₂(t) – известные функции.

Пример 3. Волновое уравнение для описания колебаний натянутой струны является примером гиперболического уравнения: 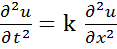, k = const.

В начальный момент времени t = t₀ обычно задаётся форма струны и распределение скорости её точек: u(x;t₀) = φ₁(x), |_г = φ₂(x), φ₁(x), φ₂(x) – известные функции, определённые на 0 < x < l.

При жёстком закреплении концов струны, краевые условия нулевые: u(0;t)=u(l;t)=0.