Задачи повышенной сложности
Алгебраическая симметрия - это особое свойство уравнений, при котором после циклической замены переменных, изменения их знаков и т.д. уравнение не меняет своего вида.
Симметрия алгебраического выражения влечет особенности в строении решений соответствующего уравнения, неравенства, системы и т.п., что нередко обыгрывается в условии задачи (накладывается, например, требование единственности решения, наличие определенного числа решений и т.п.)
В решении подобного рода задач обычно выделяются следующие два логических этапа:
1) Используя условие единственности решения (определенного числа решений и т.п.) и свойство симметрии выражения, находятся необходимые условия на параметры задачи, благодаря которым выделяется несколько возможных значений параметров.
2) На втором этапе проверяется достаточность. Обычно при этом делается подстановка параметров, отобранных в пункте 1, и для каждого из них проверяется выполнение условия задачи.
Иногда, чтобы выявить симметрию выражения, требуется предварительно его преобразовать (задачи со скрытой симметрией).
Пример 1. (Факультет психологии МГУ, 1995 г.)
Найти все значения параметра а, при которых неравенство
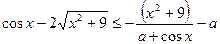
Имеет единственное решение.
Решение.
Перепишем заданное неравенство в виде
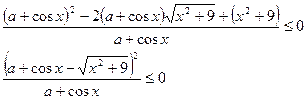
Функция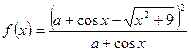 
- четная.
Поэтому, наряду с решением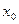 
, заданное неравенство обязательно имеет решение (- 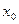). Единственным решением может быть только 
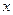=0. Если условие задачи выполняется, то необходимо
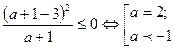
Достаточность.
Проверим достаточность условий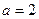 
и 
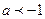
1. 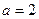, неравенство принимает вид
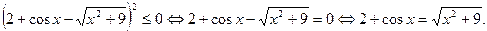
Так как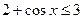 
для всех 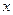и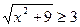 
для всех 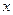, то, по методу мини-максов, последнее уравнение равносильно системе:
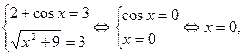
то есть при 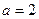неравенство имеет единственное решение 
.
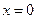2. 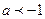, неравенство
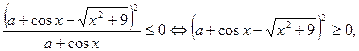
что верно для всех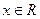 
. Достаточность не выполняется.
Ответ: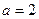
Пример 2. (Экономический факультет МГУ, 1987 г.)
Найти все значения параметра а, при каждом из которых система
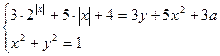
Имеет единственное решение.
Решение.
Легко убедиться, что левые и правые части каждого уравнения системы являются четными функциями относительно переменной 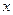. Иными словами, если 
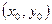- решение системы, то 
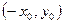- тоже решение системы.
Единственное решение системы должно иметь вид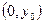 
.
Полагая в системе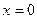 
, получим необходимое условие на значения параметра а:
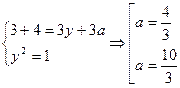
Достаточность.
1. 
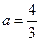, система принимает вид:
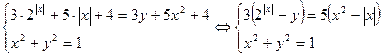
Из условия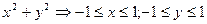 
, следовательно 
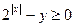и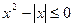 
, поэтому, согласно принципу мини-максов с А=0, последняя система равносильна системе:
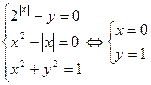
единственное решение.
2. 
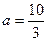, система запишется в виде:
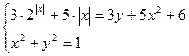
Нам заранее известно, что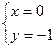 
есть решение системы.
Чтобы убедиться, что значение 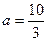не является ответом задачи, достаточно найти еще одно решение методом подбора (можно опираться на графическое представление уравнения). (1;0) – также решение системы.
Ответ: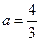
Пример 3. (филологический факультет МГУ, 1992 г.)
При каких значениях параметра а система уравнений
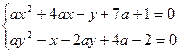
имеет единственное решение?
Решение.
Для обнаружения симметрии в системе, выделим полные квадраты в левых частях уравнений:
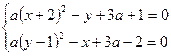
Переобозначив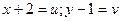 
, получаем
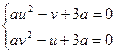(1)
Заметим теперь, что циклическая перестановка переменных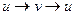 
приводит к перемене места уравнений в системе, то есть не изменяет самой системы.
Иными словами, если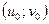 
- решение системы, то 
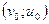- также решение системы.
Единственное решение системы, что необходимо, имеет вид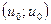 
Если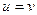 
,то оба уравнения системы (1) принимают вид:
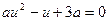(2)
1. Если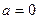 
, то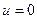 
- единственное решение;
2. Если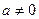 
, то квадратное уравнение (2) должно иметь единственное решение, что равносильно условию
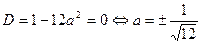
Достаточность.
1. 
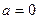
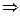
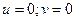– единственное решение.
2. 
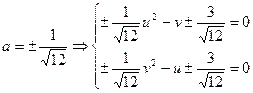(3)
Сложив уравнения системы (3), получаем
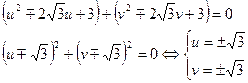
Подстановка полученных значени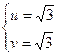й 
или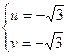 
в систему (3) приводит к верным равенствам.
Ответ: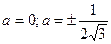 
Пример 4. (Химический факультет МГУ, 1986 г.)
Найти все значения параметра а, при каждом из которых система
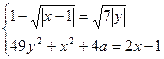
Имеет ровно четыре различных решения.
Решение.
Перепишем данную систему в виде:
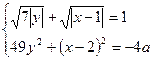(1)
После замены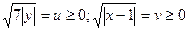 
система (1) принимает вид:
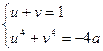(2)
Пусть 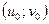- решение системы (2), причем 
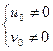(3). Каждое такое решение дает четыре различных решения системы (1):
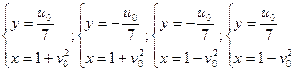(4)
Если в дополнение к условиям (3),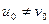 
(4), то 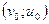- также решение системы (2), которое дает четыре новых различных решения системы (1).
Следовательно, в этом случае получается не менее восьми различных решений системы (1). Поэтому, для выполнения условий задачи, необходимо нарушить хотя бы одно из условий (3), (4).
Рассмотрим все случаи:
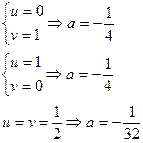
Достаточность.
1. 
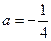, система (2) принимает вид
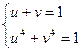(5)
Два решения (1;0); (0;1) этой системы дают четыре различных решения системы (1).
Если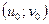 
- решение системы (5), 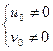, то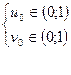 
. Тогда
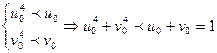
- противоречие. Значит, других решений система (5) не имеет.
2. 
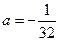, система (2)примет вид
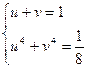(6)
Используем технический прием, называемый симметрацией. Обозначим
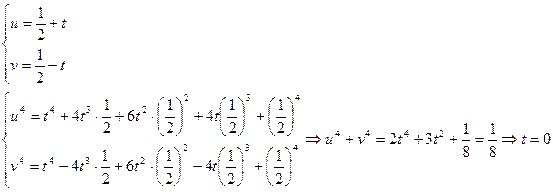
Единственное решение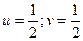 
системы (6) дает четыре различных решения исходной системы (1).
Ответ: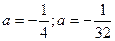 
Как мы могли убедиться на рассмотренных примерах, метод симметрии удобно применять, когда в формулировке задачи присутствует требование единственности решения уравнения, неравенства, системы и т.п. или точное указание числа решений. При этом следует обнаружить какую-либо скрытую или явную симметрию заданных выражений.
При решении подобных задач нужно также учитывать многообразие различных возможных видов симметрии и соблюдать логические этапы в рассуждениях с симметрией.
Симметрия позволяет установить необходимые условия, требующие проверки на достаточность. Эти условия существенно упрощают решение поставленной задачи.