Обозначим:
- yэкспериментальное – yэ
yрасчетное – yр
Потребуем выполнения условия: 
,
Искомое уравнение регрессии:
,
где а и в –коэффициенты регрессии.
Обозначим искомую функцию:
F (a, b) =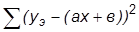 
, вычислим производные по переменным а и в. Получим формулы для вычисления коэффициентов уравнения регрессии из условия существования экстремума функции нескольких переменных
, 
, преобразуем полученные выражения. Так как требуется стремление к min суммы квадратов отклонений система примет вид:
В результате получим 
, где n- количество точек измерения
Решим систему уравнений методом Крамера:
= 
= 
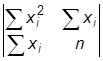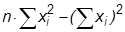, a = 
= 
b = 
, Вычислим коэффициенты: a= 
b= 
.
Или а = 
, b =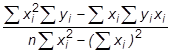 
.
Критерием точности полученных коэффициентов уравнения регрессии является сумма квадратов отклонений значений расчетной и экспериментальной функций. В результате получим значение критерия выраженного одним числом 
= 
.
Расчет коэффициента корреляции произведем по формуле:
. Коэффициент корреляции по определению является симметричным показателем связи между переменными величинами. Область его возможных изменений лежит в пределах от +1 до –1.
Результаты решения задачи должны содержать:
- исходные данные;
- необходимый графический материал;
- все выполняемые расчеты;
- явный вид уравнения регрессии;
- значение коэффициента корреляции;
- значение критерия точности решения;
- обоснованные выводы.
ПРАКТИЧЕСКИЙ ПРИМЕР
применения метода наименьших квадратов (OLS – метод)
Найти уравнение регрессии по линейному и по нелинейному закону.
Исходные данные приведены в таблице.
| Аргумент x | х1 = 1 | х2 = 2 | х3 = 3 | х4 = 4 | х5 = 5 |
| Значение уэ | у1=2,3 | у2=1,8 | у3=3,8 | у4=5,3 | у5=4,3 |
по исходным данным строим диаграмму рассеяния (Рис.1) по визуальной оценке которой выдвигается экспериментальная гипотеза. Далее выполняем предварительные расчеты.
 |  | ||||||
 |  | ||||||
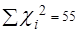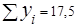n=5
, 
yp= 0,75x + 1, 25 – уравнение линейной регресcии
| x | |||||
| y | 2,75 | 3,5 | 4,25 |
x = 1 yp = 2
x = 0 yp = 1, 25
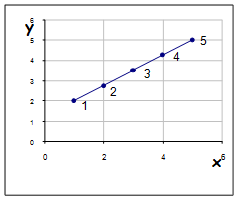
Рис. 2. Построенная линия регрессии по полученной расчетной формуле.
Рассчитаем критерий оценки построенного уравнения регрессии: сумма квадратов отклонений экспериментальных и расчетных значений (уэ-ур)2
 |
Метод выравнивания для нелинейной функции
| x | |||||
| Y | 2,3 | 1,8 | 3,8 | 5,3 | 4,3 |
| 1/y | 0,4 | 0,5 | 0,3 | 0,2 | 0,2 |
 |
Введем новую переменную
Получим закон линейного вида
 |
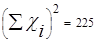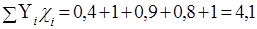
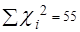
n = 5 
 |
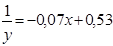Вернемся к исходной переменной
Уравнение нелинейной регрессии
Значение критерия
 |
| x | |||||
| Yp | 2,2 | 2,6 | 3,1 | 5,5 |
Вывод: в линейном законе сумма квадратов отклонений расчетной и экспериментальной точек меньше, чем в нелинейном законе (3,875<4,27), значит, принимаем линейный закон.
ЛИТЕРАТУРА (примерная)
1. Борисова Е.В. Оптимальные решения в исследовании управляемых систем: типовые модели и прикладные методы. Учебное пособие. Г.Тверь ТвГТУ, 2017
2. Боровиков В.П., Боровиков И.П. STATISTICA – Статистический анализ и обработка данных в среде Windows. – М.: Информационно-издательский дом "Филинъ", 1998.
3. Браверман Э.М., Мучник И.Б. Структурные методы обработки эмпирических данных. – М.: Наука, 1983.
4. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 1999.
5. Дубров А.М., Мхитарян В.С., Трошин Л.И. Многомерные статистические методы. – М.: Финансы и статистика, 1998.
6. Елисеева И.И., Юзбашев М.М. Общая теория статистики. – М.: Финансы и статистика, 1999.
7. Кендалл М., Стьюарт А. Статистические выводы и связи. – М.: Наука, 1973.
8. Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). – М.: Наука, 1974.
9. Надежность и эффективность в технике: Справочник в десяти томах.
10. Т.6. Экспериментальная отработка и испытания. – М.: Машиностроение, 1989.
11. Рябинин И.А. Надежность и безопасность структурно-сложных систем. – СПб.: Политехника, 2000.
12. Скрипник В.М., Назин А.Е. Оценка надежности технических систем по цензурированным выборкам. – Минск: Наука и техника, 1981.