Итак, между сигналом u (t)и его спектральной плотностью S (ω) существует однозначное соответствие, установленное соотношениями (2.33) и (2.34). Для практических целей важна связь между различными преобразованиями сигнала и соответствующими этим преобразованиям изменениями его спектральной плотности. Рассмотрим несколько основных таких радиотехнических преобразований.
Сдвиг сигнала во времени (теорема запаздывания). Пусть сигнал u 1(t)со спектральной плотностью S 1(ω) задержан на некоторое время t c. В этом случае u 2(t) = u 1(t — t с), и спектральная плотность задержанного сигнала в соответствии с прямым преобразованием Фурье (2.33) имеет вид:
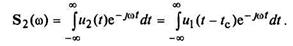
Введя новую переменную интегрирования τ = t — t c, получим
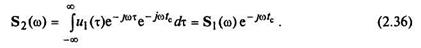
Таким образом, сдвиг сигнала во времени на некоторый интервал t c приводит лишь к изменению аргумента спектральной плотности на величину ω t c,а ее модуль остается неизменным. На практике сдвиг сигнала во времени осуществляется при аудио- и видеозаписи на различные носители. Сколь долго (теоретически) не хранилась бы такая запись, спектр (и форма) сигнала не претерпит изменений.
Сложение, усиление и ослабление сигналов (теорема линейности). Сложение, усиление и ослабление сигналов относятся к линейным операциям, поэтому к ним применимо свойство линейности. Если имеется совокупность детерминированных сигналов u 1(t), u 2(t), …, uN (t),обладающих спектральными плотностями S 1(ω), S 2(ω), …, S N (ω), то суммарному (разностному) значению сигналов u c(t)= u 1(t) + u 2(t) + … + uN (t) соответствует сумма (разность) их спектральных плотностей S c(ω) = S 1(ω) + S 2(ω) + … + S N (ω).
Данная теорема имеет элементарное доказательство: достаточно в прямое преобразование Фурье (2.33) подставить сумму исходных сигналов. В общем виде теорему линейности можно записать следующим образом:
|
|
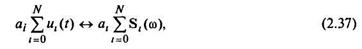
где аi — произвольные числовые коэффициенты; i = 0, 1,..., N.
Смещение спектра сигнала (теорема смещения). Смысл данной теоремы заключается в следующем: если S 1(ω) — спектральная плотность сигнала u 1(t), то спектральная плотность S 2(ω + Ω), полученная путем сдвига исходного спектра по оси частот на величину Ω, соответствует сигналу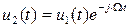 
. Действительно, согласно (2.33):
Подобное преобразование сигнала применяют в системах связи либо при переносе спектра сигнала из одной полосы частот в другую, либо при модуляции. Соотношение (2.38) показывает, что в результате таких преобразований спектр сигнала смещается на величину £2, равную частоте сдвига.
Изменение масштаба времени. Предположим, что в исходном сигнале u 1(t)изменен масштаб времени таким образом, что аргумент t умножен на некоторый постоянный коэффициент b и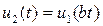 
. Если b >1, то происходит «сжатие» исходного сигнала; если же 0 < b <1 — исходный сигнал «растягивается» во времени. Докажем это положение.
Спектральная плотность измененного сигнала
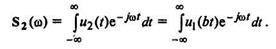
Введя новую переменную τ = bt, получим
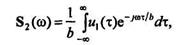
откуда
Таким образом, увеличение длительности импульсного сигнала любой формы в раз b сопровождается сжатием его спектра во столько же раз, и наоборот, уменьшение длительности приводит к расширению спектра.