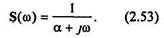Спектры некоторых неинтегрируемых сигналов

Из курса математики известно, что ряд широко применяемых (в частности в ра­диоэлектронике и технике связи) сигналов (функций) не удовлетворяют условиям, абсолютной интегрируемости (сходимости):

поэтому их прямое преобразование Фурье определить сложно. Однако в теории сигналов известна функция, некоторые свойства которой позволяют устранить дан­ное препятствие.

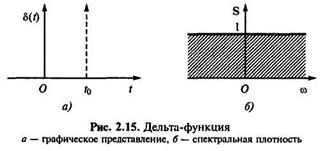
Дельта-функция и ее спектр. Рассмотрим теоретическую модель бесконечно короткого импульса с бесконечно большой амплитудой (рис. 2.15, а), анали­тически определяемого формулой:

Площадь такого импульса всегда равна единице:

Функцию δ(t) называют дельта-функцией, единичным импульсом, функцией Дирака,и она имеет физическую размерность циклической частоты − с^-1. При сдвиге дельта-функции порей времени на интервал t ₀ (см. рис. 2.15, а) определения (2.41) и (2.42) необходимо записать в более общей форме:

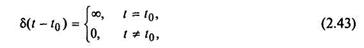
Дельта-функция обладает важнейшим свойством, благодаря которому она получила широкое применение в математике, физике, радиотехнике и теории связи. Пусть имеется некоторая непрерывная функция времени f (t). Тогда, согласно формулам (2.43) и (2.44), справедливо соотношение

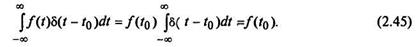
Формула (2.45) становится понятной, если учесть, что по определению функция δ(t − t ₀) будет равна нулю на всей оси времени, кроме точки t = t ₀.Это позволяет сделать интервал интегрирования бесконечно малым, включающим в себя точку t ₀. В этом интервале функция f (t)принимает един­ственное постоянное значение f (t ₀)в точке t = t ₀,которое можно вынести за знак интеграла. Соотношение (2.45) характеризует фильтрующее (выделяющее, или стробирующее — от слова «строб» — короткий прямоугольный импульс, применяемый в РЛС) свойство дельта-функции.

Спектральную плотность дельта-функции δ(t − t ₀) определим с помощью прямого преобразования Фурье (2.33):

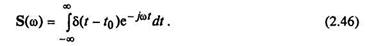
Используя фильтрующее свойство (2.45), находим:

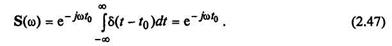
При t ₀ = 0 спектральная плотность S (ω) = 1. Итак, дельта-функция имеет равно­мерный (сплошной и бесконечный) спектр с единичной амплитудой на всех часто­тах (рис. 2.15, б).Следует иметь в виду, что правая часть равенства (2.47) является размерной единицей — это единичная площадь импульса. Если функцией 5(0 явля­ется импульс напряжения, то размерность спектральной плотности S (ω) — вольт·секунду (В·с).

Физически интерпретировать свойства и параметры дельта-функции достаточно просто. В момент возникновения импульса (/ = 0) все элементарные гармонические составляющие бесконечного спектра складываются когерентно (синфазно), по­скольку в соответствии с последней формулой спектральная плотность дельта-функции вещественна. Поэтому при t = 0 наблюдается бесконечно большая ампли­туда импульса.

Понятие дельта-функции широко используется в радиоэлектронике и теории свя­зи при исследовании воздействия очень коротких импульсов напряжения на линей­ные цепи. При этом не обязательно, чтобы длительность реального импульса была бесконечно мала, а амплитуда бесконечно велика. Оказывается достаточным усло­вие, чтобы длительность импульса была много меньше периода собственных коле­баний цепи.

Дельта-функцию можно представить в виде обратного преобразования Фурье (2.34) от ее спектральной плотности S (ω) = 1:

Учитывая условие взаимозаменяемости (дуальности) частоты ω и времени t, по­следнее выражение можно записать следующим образом:

Перемена знака в показателе степени экспоненты в этом случае не влияет на значение интеграла (вследствие взаимозаменяемости частоты и времени).

Спектральная плотность гармонического сигнала. Определим спектральную плотность гармонического (положим, что косинусоидального) сигнала единичной амплитуды 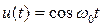. Подставив в прямое преобразование Фурье (2.33) заданный сигнал, и воспользовавшись формулой Эйлера 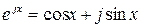, находим:

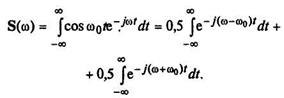
На основании выражения (2.49) последнее соот­ношение можно записать в следующем виде:

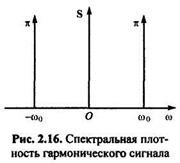
Как и следовало ожидать, гармоническому сигналу с конечной (в данном случае единичной) амплитудой соответствует дискретный спектр, состоящий из двух ли­ний бесконечно большой амплитуды в виде дельта-функций, расположенных сим­метрично относительно нуля на частотах −ω₀ и ω₀(рис. 2.16).

По аналогии с косинусоидальным сигналом нетрудно показать, что синусои­дальному сигналу u (t)= sinω₀ t отвечает спектральная плотность

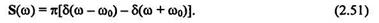
Здесь знак минус появляется вследствие нечетности функции синусоидального сигнала.

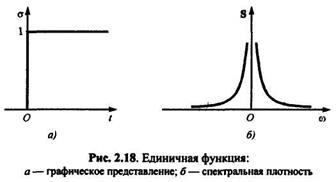
Спектральная плотность экспоненциального импульса. Данный импульс от­носится к сигналам с «полубесконечной» длительностью (рис. 2.17, а) и при еди­ничной амплитуде описывается как:

где α> 0 — вещественный параметр.

Спектральная плотность экспоненциального импульса

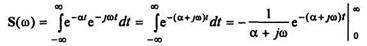
Подстановка пределов интегрирования дает следующий результат для спек­тральной плотности (рис. 2.17, б):