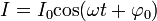Методы расчета электрических цепей
1. Электрические цепи и их элементы. Линейные и нелинейные, активные и пассивные цепи. Активное сопротивление, емкость и индуктивность.
Реальные элементы цепи могут быть описаны алгебраическими или дифференциальными уравнениями, связывающими напряжения и токи на зажимах этих элементов. Такое описание может быть сделано с определенной степенью точности при идеализации физических процессов в элементах; второстепенные с определенной точки зрения процессы при этом не учитываются.
Если элемент цепи характеризуется линейными алгебраическими или дифференциальными уравнениями (при упомянутой ранее идеализации), то его называют линейным. Коэффициенты, связывающие напряжения и токи и их производные, представляют собой параметры элемента. Параметры линейного элемента могут быть постоянными (стационарный элемент) или могут изменяться в зависимости от времени по какому-либо закону (нестационарный, параметрический элемент).
Если элемент цепи описывается нелинейными алгебраическими или дифференциальными уравнениями, то он называется нелинейным. Нелинейные элементы могут быть также параметрическими.
Цепи, содержащие только линейные элементы, называют линейными цепями. Основное свойство таких цепей — применимость принципа наложения, заключающегося в том, что результирующая реакция линейной цепи на несколько приложенных одновременно возмущений равна сумме реакций, обусловленных каждым возмущением в отдельности.
Если цепь содержит один или несколько параметрических элементов, то ее называют параметрической (нестационарной).
Аналогично, если цепь содержит один или более нелинейных элементов, то ее называют нелинейной. Для нелинейной цепи в общем случае неприменим принцип наложения.
Можно говорить также об активных и пассивных цепях. Цепь считают активной, если по отношению к некоторым зажимам она является источником энергии. Такая цепь содержит активные элементы. В противном случае цепь называют пассивной
Индуктивность
Вокруг всякого проводника с током образуется магнитное поле, которое характеризуется вектором магнитной индукции В и магнитным потоком Ф: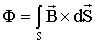 
Если поле образуют несколько (w) проводников с одинаковым током, то используют понятие потокосцепления ψ: ψ = w Ф. Отношение потокосцепления к току, который его создает называют индуктивностью катушки L = ψ / i. При изменении во времени потокосцепления согласно закону Фарадея возникает ЭДС самоиндукции eL = - dψ / dt. С учетом соотношения для eL получаем eL = - L · di / dt. Эта ЭДС всегда препятствует изменению тока (закон Ленца). Поэтому, чтобы через проводники все время тек ток, необходимо к проводникам прикладывать компенсирующее напряжение uL = -eL. uL = L · di / dt. Это соотношение является аналогом закона Ома для индуктивности. Конструктивно индуктивность выполняется в виде катушки с проводом.
Единицей измерения индуктивности является Генри (Гн).
Емкость
Все проводники с электрическим зарядом создают электрическое поле. Характеристикой этого поля является разность потенциалов (напряжение). Электрическую емкость определяют отношением заряда проводника к напряжению C = Q / UC. С учетом соотношения i = dQ / dt получаем формулу связи тока с напряжением i = C · duC / dt. Для удобства ее интегрируют и получают uC = 1 / C · ∫ i dt. Это соотношение является аналогом закона Ома для емкости. Конструктивно емкость выполняется в виде двух проводников разделенных слоем диэлектрика. Форма проводников может быть плоской, трубчатой, шарообразной и др.
Единицей измерения емкости является фарада: 1Ф = 1Кл / 1В = 1Кулон / 1Вольт.
Оказалось, что фарада является большой единицей, например, емкость земного шара равна ≈ 0,7 Ф. Поэтому чаще всего используют дробные значения
1 пФ = 10–12 Ф, (пФ – пикофарада);
1 нФ = 10–9 Ф, (нФ – нанофарада);
1 мкФ = 10–6 Ф, (мкФ – микрофарада).
2. Идеальные источники напряжения и тока. Метод эквивалентного источника.
Источник ЭДС (идеальный источник напряжения) — двухполюсник, напряжение на зажимах которого постоянно (не зависит от тока в цепи). Напряжение может быть задано как константа, как функция времени, либо как внешнее управляющее воздействие.
В простейшем случае напряжение определено как константа, то есть напряжение источника ЭДС постоянно.
Идеальный источник напряжения (источник ЭДС) является физической абстракцией, то есть подобное устройство не может существовать. Если допустить существование такого устройства, то ток I, протекающий через него, стремился бы к бесконечности при подключении нагрузки, сопротивление RH которой стремится к нулю. Но при этом получается, что мощность источника ЭДС также стремится к бесконечности, так как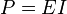 
. Но это невозможно, по той причине, что мощность любого источника энергии конечна.
Идеальный источник электрического тока – это элемент, ток в котором не зависит от параметров электрической цепи, к которой он подключен. Внутреннее сопротивление идеального источника тока равно бесконечности.
Напряжение на клеммах идеального источника тока зависит только от сопротивления внешней цепи:
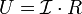
Мощность, отдаваемая источником тока в сеть, равна:
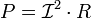
Так как для источника тока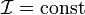 
, напряжение и мощность, выделяемая им, неограниченно растут при росте сопротивления.
Метод эквивалентного источника
Метод эквивалентного источника позволяет произвести частичный анализ электрической цепи. Например, определить ток в какой-либо одной ветви электрической цепи или исследовать поведение этой ветви при изменении ее сопротивления. Применение данного метода может оказаться полезным как при частичном расчете сложных электрических цепей, так и простых.
Метод эквивалентного источника применяют в следующей последовательности:
Вычерчиваем принципиальную схему и все ее элементы.
Заданную условием задачи схему разбивают на две части: ветвь (или участок электрической цепи) в которой требуется найти значение тока и остальную часть схемы.
Производят замену активного двухполюсника на эквивалентный источник напряжения или тока.
Для замены активного двухполюсника на источник напряжения необходимо рассчитать значения Еэк и Rэк, а для замены на источник тока рассчитывают Jэк и Rэк. Для нахождения значения E эк необходимо разомкнуть ветвь, в которой требуется найти значение тока, и определить значение напряжения на зажимах a и b (см. рис.) путем расчета схемы активного двухполюсника. Полученное напряжение численно будет равно Е эк (в некоторых учебниках это напряжение называют напряжением холостого хода). Для нахождения значения J эк необходимо замкнуть накоротко зажимы a и b и путем расчета схемы активного двухполюсника найти значение тока через перемычку. Полученное значение тока численно будет равно J эк (в некоторых учебниках этот ток называют током короткого замыкания). Внутреннее сопротивление R эк эквивалентного источника равно сопротивлению элементов активного двухполюсника, из которого исключены все источники (источники ЭДС заменены короткозамкнутыми участками, а источники тока отключены), со стороны зажимов a и b. Расчет схемы активного двухполюсника для нахождения значений E эк, J эк и R эк ведут любым удобным способом из числа доступных.
Находят значение тока в заданной ветви, применив одно из следующих соотношений:
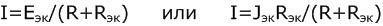
3. Методы расчета электрических цепей. Законы Ома и Кирхгофа.
Расчет резистивных цепей методом составления уравнений Кирхгофа. С помощью законов Кирхгофа можно рассчитать токи в сколь угодно сложных цепях. Для этого необходимо проделать следующее: определить количество ветвей в заданной цепи; задаться предполагаемыми токами во всех ветвях и направлениями обходов в контурах (например, по часовой стрелке); по первому закону составитьn-1 уравнений, где n – количество узлов цепи; определить количество элементарных контуров в цепи; составить по второму закону Кирхгофа m уравнений, где m – число элементарных контуров.
Расчет сложной электрической цепи методом контурных токов выполняется в следующем порядке:
1. Произвольно выбирают направление контурных токов, обозначают их и для удобства считают такое же направление обхода по контурам.
2. Составляют уравнения по второму закону Кирхгофа с контурными токами. При этом если на участке цепи действует несколько контурных токов, то падение напряжения на этом участке равно алгебраической сумме падений напряжений, созданных каждым контурным током.
Расчет электрической цепи методом суперпозиции. При применении метода наложения для расчета сложных электрических цепей с несколькими источниками вначале предполагают, что в электрической цепи действует только одна ЭДС, и определяют токи, созданные ею. Эти токи называются частичными. При расчете частичных токов должны учитываться внутренние сопротивления источников, исключенных в этом случае из схемы.
После этого оставляют в электрической цепи какую-либо другую ЭДС и исключают все остальные. При этом опять определяют частичные токи. Таким способом находят поочередно частичные токи, созданные каждой ЭДС отдельно. Затем производят наложение частичных токов, при котором определяют величину и направление действительных токов на основании того, что действительный ток в любом участке электрической цепи равен алгебраической сумме частичных токов, гдеI′ и I″ частичные токи т.е.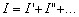 
Метод суперпозиции основан на принципе независимости действия электродвижущих сил различных источников. Он применим только к линейным цепям, т.е. таким, сопротивление которых не зависит от величины протекающего тока или приложенного напряжения. Процессы в этих цепях описываются уравнениями первой степени. Если в цепи имеется хотя бы один нелинейный элемент или в выражении, описывающем процессы в цепи, имеется хотя бы одна переменная величина со степенью выше первой, то метод суперпозиции принципиально использован быть не может.
Метод эквивалентных сопротивлений
(метод свертывания и развертывания цепи).
Этот метод применяется только для электрических цепей содержащих один источник питания. Для расчета, отдельные участки схемы, содержащие последовательные или параллельные ветви, упрощают, заменяя их эквивалентными сопротивлениями. Таким образом, цепь свертывается до одного эквивалентного сопротивления цепи подключенного к источнику питания.
Затем определяется ток ветви, содержащий ЭДС, и схема разворачивается в обратном порядке. При этом вычисляются падения напряжений участков и токи ветвей.
Зако́н О́ма — физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока и сопротивлением проводника.
Закон Ома для полной цепи:
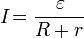, (2)
где:
· 
— ЭДС источника напряжения(В),
· 
— сила тока в цепи (А),
· 
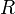— сопротивление всех внешних элементов цепи (Ом),
· 
— внутреннее сопротивление источника напряжения (Ом).
Из закона Ома для полной цепи вытекают следствия:
· При r<<R сила тока в цепи обратно пропорциональна её сопротивлению. А сам источник в ряде случаев может быть назван источником напряжения
· При r>>R сила тока от свойств внешней цепи (от величины нагрузки) не зависит. И источник может быть назван источником тока.
Первое правило Кирхгофа (правило токов Кирхгофа) гласит, что алгебраическая сумма токов в каждом узле любой цепи равна нулю. При этом втекающий в узел ток принято считать положительным, а вытекающий — отрицательным:
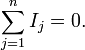
Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.
Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:
для постоянных напряжений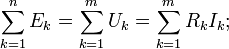 
для переменных напряжений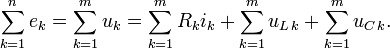 
4. Метод контурных токов.
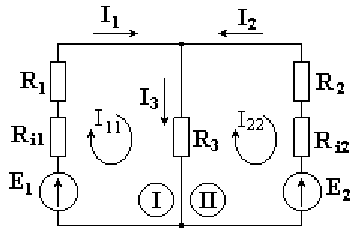Метод непосредственного применения законов Кирхгофа громоздок. Имеется возможность уменьшить количество совместно решаемых уравнений системы. Число уравнений, составленных по методу контурных токов, равно количеству уравнений, составляемых по второму закону Кирхгофа.
Метод контурных токов заключается в том, что вместо токов в ветвях определяются, на основании второго закона Кирхгофа, так называемые контурные токи, замыкающиеся в контурах. Выбираются независимые контуры, и задаются произвольные направления контурных токов.
В нашем случае эти токи направлены по часовой стрелке. Направление обхода контура совпадает с направлением контурных токов. Уравнения для этих контуров имеют следующий вид:
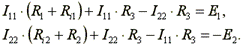
Перегруппируем слагаемые в уравнениях
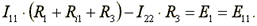(4.4)
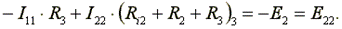(4.5)
Суммарное сопротивление данного контура называется собственным сопротивлением контура.
Собственные сопротивления контуров схемы
, 
.
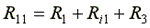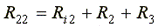Сопротивление R3, принадлежащее одновременно двум контурам, называется общим сопротивлением этих контуров.
,
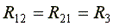где R12 - общее сопротивление между первым и вторым контурами;
R21 - общее сопротивление между вторым и первым контурами.
E11 = E1 и E22 = E2 - контурные ЭДС.
В общем виде уравнения (4.4) и (4.5) записываются следующим образом:
,
.
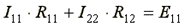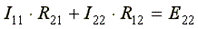Собственные сопротивления всегда имеют знак "плюс".
Общее сопротивление имеет знак "минус", если в данном сопротивлении контурные токи направлены встречно друг другу, и знак "плюс", если контурные токи в общем сопротивлении совпадают по направлению.
Решая уравнения (4.4) и (4.5) совместно, определим контурные токи I11 и I22, затем от контурных токов переходим к токам в ветвях.
Ветви схемы, по которым протекает один контурный ток, называются внешними, а ветви, по которым протекают несколько контурных токов, называются общими. Ток во внешней ветви совпадает по величине и по направлению c контурным. Ток в общей ветви равен алгебраической сумме контурных токов, протекающих в этой ветви.
.
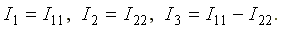5. Метод узловых потенциалов.
Метод узловы́х потенциалов — метод расчета электрических цепей путём записи системы линейных алгебраических уравнений, в которой неизвестными являютсяпотенциалы
в узлах цепи. В результате применения метода определяются потенциалы во всех узлах цепи, а также, при необходимости, токи во всех ветвях.
6. Основные характеристики синусоидального тока. Максимальное, среднее и действующее значения величин.
Синусоидальным током называют ток, изменяющийся во времени по синусоидальному закону:
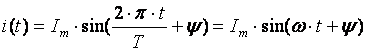
Ток i(t) называют мгновенным. Максимальное значение тока называют амплитудой и обозначают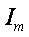 
. Период 
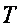– это время, за которое совершается одно полное колебание. Частота равна числу колебаний в секунду 
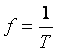, единица частоты 
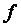- герц (Гц).
Угловая частота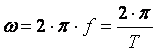 
, единица угловой частоты рад/с или 
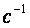. Аргумент синуса, т.е. 
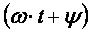, называют фазой. Фаза характеризует состояние колебания в данный момент времени 
.
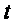Начальная фаза тока -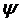 
.
Любая синусоидальная функция характеризуется тремя величинами: амплитудой, угловой частотой и начальной фазой.
Среднее и действующее значение синусоидальных тока и ЭДС.
Принято среднее значение функции времени определять за период
Для синусоидальной функции среднее значение за период равно нулю.
Используется также понятие среднего значения синусоидальной функции за полпериода:
.
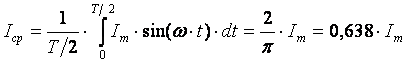Аналогично, среднее значение ЭДС за полпериода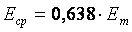 
.
Действующим значением синусоидальной функции называется ее среднеквадратичное значение за период
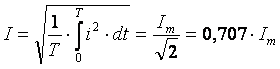
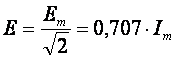
Большинство измерительных приборов амперметров и вольтметров показывают действующее значение измеряемой величины.
7. Метод векторных диаграмм и метод комплексных чисел для расчета цепей.
Векторная диаграмма — графическое изображение меняющихся по закону синуса (косинуса) величин и соотношений между ними при помощи направленных отрезков — векторов. Векторные диаграммы широко применяются в электротехнике, акустике, оптике, теории колебаний и так далее.
Гармоническое (то есть синусоидальное) колебание может быть представлено графически в виде проекции на некоторую ось (обычно берут ось координат Оx) вектора, вращающегося с постоянной угловой скоростью ω. Длина вектора соответствует амплитуде, угол поворота относительно оси (Ox) - фазе.
Сумма (или разность) двух и более колебаний на векторной диаграмме представлена при этом (геометрической) суммой[1] (или разностью) векторов этих колебаний. Мгновенное значение искомой величины определяется при этом проекцией вектора суммы на ось Оx, амплитуда - длиной этого вектора, а фаза - углом его поворота относительно Ox.
Наиболее стандартный, распространенный и простой случай применения векторных диаграмм к электрическим схемам - это последовательные и параллельные цепи, состоящие из линейных элементов (резисторов, конденсаторов и элементов, обладающих индуктивностью[8]).
Основой выполнения типичного расчета в терминах, исключающих явное использование комплексных чисел, является понятие реактивного сопротивления, которое вводится для конденсаторов и индуктивных элементов (катушек индуктивности), исходя из основных физических уравнений[9], позволяющих связать ток через элемент и напряжение на нем (или ЭДС в нем):
· для конденсатора:
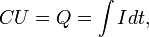
· для индуктивности:
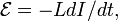притом 
Затем в эти уравнения подставляют синусоидальный ток:
и получают
· для конденсатора:
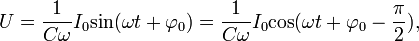
· для индуктивности:
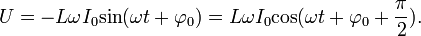
Заметим, что формулы очень похожи на обычный закон Ома
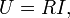
за исключением двух моментов: 1) если обычное (называемое в данном контексте активным) сопротивление R не вызывает изменения фазы напряжения по сравнению с током (они синфазны), то напряжение на конденсаторе запаздывает по фазе относительно тока на 90°, а на индуктивности напряжение опережает ток по фазе на те же 90°; 2) коэффициент, на который домножается ток, чтобы получить напряжение, как раз и называемый реактивным сопротивлением зависит и у конденсатора, и у индуктивности от частоты тока (и зависит разным, обратным, образом).
Таким образом, мы знаем, как изобразить на векторной диаграмме напряжение на конденсаторе, индуктивности или резисторе, если известен ток (то есть его вектор уже нарисован). А именно: для конденсатора мы должны умножить (масштабировать) вектор, изображающий ток, на коэффициент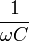 
и повернуть его на 90° в положительном направлении (против часовой стрелки), для индуктивности же мы должны умножить вектор тока на 
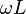и повернуть его на 90° в отрицательном направлении (по часовой стрелке). Так мы получим вектор, изображающий напряжение, для конденсатора и индуктивности, если мы знаем вектор тока. Для резистора же ("активного сопротивления"), чтобы построить вектор, изображающий напряжение, вектор, изображающий ток, надо только умножить на R, не меняя его направления.
8. Символический метод анализа цепей переменного тока.
В тетради.
9. Законы Ома и Кирхгофа в комплексной форме.
Под законом Ома в комплексной форме понимают: Í = Ú / Z