Колебанием называется процесс, при котором какая-либо физическая величина, характеризующая этот процесс, последовательно изменяется то в одну, то в другую сторону около некоторого своего среднего значения. Например, на качелях, подвешенных на веревках, человек отклоняется то вперед и вверх, то назад и вверх от положения равновесия. Говорят, что качели являются колебательной системой.
Таким образом, механической колебательной системой называется совокупность тел, в которой могут происходить колебательные процессы.
Наиболее простыми механическими колебательными системами являются: вертикальный пружинный маятник, который образуют Земля, штатив, пружина и груз; физический маятник, образованный Землей, штативом и шариком на нити; и горизонтальный пружинный маятник — это два штатива, две пружины и шарик.
Колебательный процесс в системе может происходить под действием как внутренних, так и внешних сил. Если колебания в системе происходят только под действием внутренних сил, то их называют свободными колебаниями.
А если колебания тела повторяются через определенный промежуток времени, то их называют периодическими.
Рассмотрим условия, которые необходимы для того, чтобы в системе могли возникнуть свободные колебания:
1) Необходимо наличие положения устойчивого равновесия.

2) Необходимо наличие у тела избыточной механической энергии по сравнению с ее энергией в положении устойчивого равновесия, так как самопроизвольно (то есть без внешнего воздействия) система не может выйти из положения равновесия.
3) на тело должна действовать возвращающая сила, то есть сила, всегда направленная к положению устойчивого равновесия.
|
|
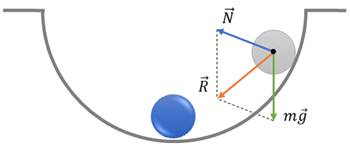
4) В идеальных колебательных системах должны отсутствовать силы сопротивления.
Теперь рассмотрим некоторые важные характеристики колебательного движения.
Периодом колебания называется промежуток времени, в течение которого совершается одно полное колебание.
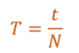
Частота колебаний — это величина, обратная периоду, равная числу колебаний, совершенных системой за одну секунду.
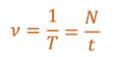
В СИ период измеряется в секундах, а частота — в герцах.
Смещением называется любое отклонение физической величины от ее значения в положении равновесия и измеряемая расстоянием от положения равновесия до положения точки в заданный момент времени.
Амплитудой называется максимальное смещение тела от положения равновесия.
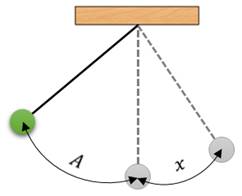
Простейшим видом колебаний являются гармонические колебания. Термин «гармонические колебания» впервые был введен в науку швейцарским физиком Даниилом Бернулли. Гармоническими называются колебания, при которых какая-либо величина изменяется с течением времени по закону синуса или косинуса.
Чтобы установить основные кинематические признаки гармонических колебаний, рассмотрим их математическую модель на примере изменения физических величин, характеризующих движение материальной точки по окружности с постоянной угловой скоростью. Начало координат поместим в центре окружности радиуса R. Пусть в начальный момент времени материальная точка находилась в положении M 0 и ее радиус-вектор составлял с осью Ox угол j 0.
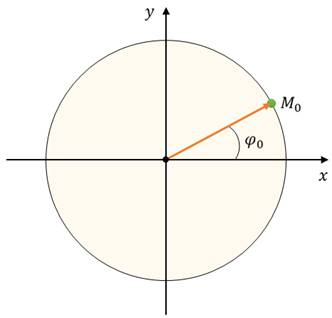
Через промежуток времени t точка переместится в положение M, а ее радиус-вектор при этом повернется на угол D j и составляет в данный момент с осью Ox угол
|
|
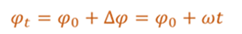

Запишем теперь координаты точки в этот момент времени


Теперь расположим перпендикулярно друг к другу два экрана и будем освещать движущийся шарик. На вертикальном экране тень от шарика будет двигаться вдоль оси Oy по закону:

То есть совершать колебания возле начала координат. На горизонтальном экране тень шарика будет двигаться вдоль оси Ox по закону:

И также совершать колебания около начала координат.
Величина, стоящая под аргументом синуса или косинуса, или, в выбранной системе отсчета, угол между радиус-вектором и осью абсцисс называется фазой колебания.

Начальная фаза колебания j 0 характеризует положение точки в начальный момент времени.
Тогда мгновенные значения координат x и y, можно рассматривать как смещения шарика от нулевого значения, а модуль амплитудного значения для обеих координат равен радиусу окружности.
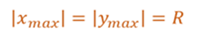
Таким образом, кинематический закон любого гармонического движения можно представить в виде:
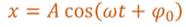
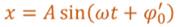
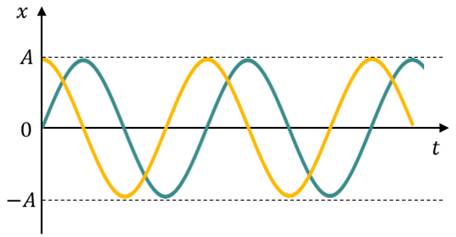
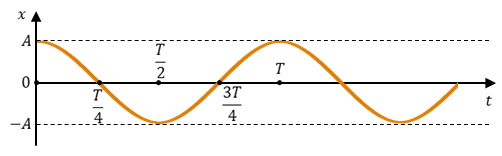
Следовательно, графически зависимость смещения колеблющейся точки от времени изображается косинусоидой или синусоидой.
В записанных уравнениях w — это циклическая (или круговая) частота, которая показывает, сколько колебаний совершает материальная точка за 2 p секунд. Соответственно, в системе СИ она измеряется в радианах на секунду.

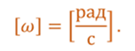
Рассмотрим, как изменяются проекции скорости и ускорения колеблющейся точки со временем для случая, когда начальная фаза колебаний равна нулю.
Начнем со скорости. Для этого найдем первую производную по времени от кинематического закона гармонических колебаний.
|
|

В полученном выражении произведение циклической частоты и амплитуды колебаний — это есть амплитуда проекции скорости на ось координат.
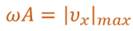
Таким образом видим, что при гармонических колебаниях проекция скорости тела на координатную ось тоже изменяется по гармоническому закону с той же частотой, но с другой амплитудой и опережает по фазе смещение на p /2.
Начнем со скорости. Для этого найдем первую производную по времени от кинематического закона гармонических колебаний.

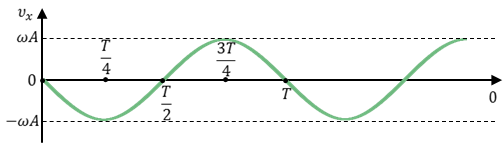
Теперь рассмотрим ускорение. Для этого найдем производную от проекции скорости по времени.
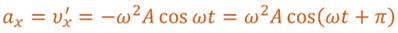
Величина, равная произведению квадрата циклической частоты и амплитуды колебаний, является амплитудой проекции ускорения.
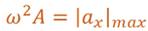
Как видно из формулы, при гармонических колебаниях проекция ускорения опережает смещение по фазе на p. Говорят, что проекция ускорения изменяется с течением времени в противофазе изменению координаты.
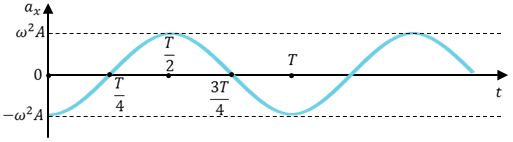
Учитывая кинематический закон гармонического движения получим, что при гармонических колебаниях проекция ускорения прямо пропорциональна смещению и противоположна ему по знаку, то есть направлено в сторону, противоположную смещению.
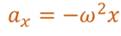
Так как проекция ускорения — это вторая производная от смещения по времени, то последнее соотношение можно записать в виде:
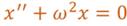
Это уравнение называется уравнением гармонических колебаний.