Трехмерный потенциальный барьер. Квазнстационарные состояния.

Рассмотрение задачи о прохождении через потенциальный барьер, отличалось той особенностью, что речь шла о потоке частиц, приходящих из бесконечности и встречающих на своем пути потенциальный барьер. В дальнейшем (теория радиоактивного распада, автоионизация атомов) нам встретятся такие случаи, когда речь будет идти о потоке частиц, выходящих из неко­торой ограниченной обла­сти пространства (ядро атома, атом), окруженной, потенциальным барьером. Пусть сфера с центром в 0 и радиусом r₀ (рис. 1,а)

 

Рис.4.1. Потенциальный барьер, ограничивающий замкнутую область (r < r₀)

 

Есть та поверхность, на которой потенциальная энергия U (r) принимает максимальное значение, так что для r < r₀, U < U_m и для r > r₀, U < U_m. Соответствующий пример графика U(г) дан на рис. 1, б. Допустим, что нас интересует прохождение через барьер частиц, первоначально находившихся внутри него. Соответственно предположению, что частицы, падающие извне, отсутствуют (нет «бомбардировки»), мы должны взять вне барьера лишь уходящие волны.

(4.1)

Это условие мы будем называть условием излучения. Ясно, что уравнение Шредингера

(4.2)

в этом случае может иметь лишь нестационарные решения. Дей­ствительно, применим закон сохранения числа частиц к сфере радиуса r:

(4.3)

Из (4.1) имеем,

(4.4)

и, стало быть,

 

(4.5)

т. е. среднее число частиц в объеме сферы V убывает, так что ψ не может гармонически зависеть от времени.

Задачу об истечении частиц из барьера можно решать, исходя из уравнения (4.2) с начальным условием. таким, что функция ψ (r, 0) отлична от нуля лишь внут­ри барьера (чтобы выразить тот факт; что при t = 0 частица нахо­дилась внутри барьера). Можно, од­нако, исходить из другого условия, до некоторой степени противоположного, именно считать, что истечение частиц происходит уже давно и зна­чительная часть их уже находится вне барьера.

 

Рис 4.2 Потенциальный барьер, ограничивающий замкнутую область (r < r₁) и имеющий простую прямоугольную форму.

 

Такой подход к реше­нию мы рассмотрим подробнее. Он удобен тем, что допускает разделе r и t в уравнении (4.2) Положим сразу

 

При этом величина Е будет комп­лексной, и ее нельзя рассматривать как энергию частиц. Положим

(4.7)

Тогда среднее число частиц в объеме V₀, заключенном внутри барьера, согласно (4.6) и (4.7), будет

т. е.

(4.8)

Величина λ - константа распада. Подста­новка (46) в (4.2) дает

(99.9)

 

Чтобы выяснить принципиальную сторону дела, мы рассмотрим схематичный пример, взяв форму барьера U (r), изображенную на рис. 4.1. Рассмотрим далее, для простоты, состояния с орбиталь­ным моментом, равным нулю: / = 0. Тогда, полагая

(4.10)

мы получим из (4.9)

(99.11)

Согласно нашему предположению о виде U (г) уравнение (99.11) разобьется на три;

(99.12) (99.12")(99.12'):

 

где:

(99.13):

Решения этих уравнений имеют вид

(99.14) (99.14') (99.14")

Из условия конечности ψ в нуле следует, что

(99.15)

Кроме того, условие излучения дает b = 0 (только уходящие волны). Краевые условия на границах r = r ₁ и r=r ₂, как мы установили в § 1,сводятся к равенству функций и их первых производных

(99.16) (99.16’) (99.17) (99.17')

На этот раз мы имеем четыре однородных уравнения для четырех коэффициентов A, α, β, а. Поэтому необходимо, чтобы определи­тель ∆ системы уравнений (4.16) и (4.17) обращался в нуль. Несложные вычисления дают

(4.18)

где l означает ширину барьера r₂ - r ₁ (4.18) есть трансцендент­ное уравнение для k. Определим его корни приближенно, считая ql » l. Тогда в нулевом 'приближении можно отбросить член с e ^-gl, и мы получаем

(4.19)

Это — точное уравнение для нахождения собственных значений потенциальной ямы (0, r₁, U_m), изображенной на рис. 4.2 и полу­чаемой из потенциального барьера рис. 4.2 при r₂ = ∞. В такой потенциальной яме имеются дискретные уровни энергии (для E<.U_m). Если корни уравнения (4.19) обозначить через k₀₁, k_O2,… k_n,…, то энергия этих уровней будет (согласно (4.13)) равна

(99.20)

Корни действительны, если λ = 0, и по порядку величины равны . В этом случае мы имеем стационарные состояния. При конечной ширине барьера асимптотическое поведение потенциаль­ной энергии таково, что U(r)_r→∞ < Е, и вместо дискретного спектра (4.20) мы получаем непрерывный. Однако условие излу­чения выбирает из непрерывного спектра уровни, близкие к Е_оп, но они не будут теперь стационарными (λ_п ≠ 0). При малых λ_п они будут почти стационарными. Это — квазистационарные уровни. Определим величину λ_п, считая ее малой. Для этого разложим член с e^ql в (4.18) по степеням ∆k = k — ko, где k₀ — один из корней уравнения (4.19), для ста­ционарных состояний потенциальной ямы, а в член с e^-gl под­ставим k = k₀; замечая, что

получим

Отсюда находим ∆k

При этом малую поправку к действительной части k₀ мы также
можем опустить, как не представляющую интереса. Мнимая же
часть будет равна.

' (99.21)

Пренебрегая также малой поправкой к действительной части, k в (4.13), мы можем положить . Из (4.13) получаем

. (4.22)

 

Сравнивая это с предыдущим выражением для ∆k, мы находим

(4.23)

Имея в виду, что есть скорость частицы v₀ внутри барьера и что k₀ ≈ 1/r ₁ = 1/r ₀ (r_o радиус ямы), мы получаем из (4.23) И (4.13)

(4.24)

Эта формула имеет простое наглядное толкование. есть число ударов частицы о внутреннюю стенку барьера в 1 сек, а экспо­ненциальный множитель есть коэффициент прозрачности.

Отметим еще некоторые особенности рассмотренной задачи. Мнимое значение волнового вектора к приводит к тому, что интенсивность излучаемой волны неограниченно растет по мере удаления от потенциального барьера

.

Рост ψ₁₁₁ вытекает из требования, чтобы имелось только, излучение, и отвечает тому факту, что на больших расстояниях находятся частицы, выле­тевшие раньше, еще тогда, когда интенсивность | ψ₁ |² внутри самого барьера была больше. Однако в нашем методе решения мы не учли того обстоятельства, что излучение на самом деле когда-то началось (а не длилось все время от t=∞) и что к моменту начала излучения | ψ₁ |² было конечно. Поэтому наш вывод о том, что ψ₁₁₁ > ∞ при r → ∞, вывод, относящийся к частицам, выле­тевшим очень давно, неверен, и само найденное, решение справедливо; лишь для небольших r, именно для

Отметим, что в связи с формулой (4.7) в литературе часто говорят о мнимой энергии. Следует иметь в виду, что такое выражение имеет лишь чисто формальный смысл. Найденное вами состояние

 

не есть стационарное состояние с определенным значением энергии (стацио­нарные состояния гармонически зависят от времени).

Чтобы определить вероятность найти то или иное значение энергии Е в этом состоянии, нужно разложить ψ (г, t) по соб­ственным функциям ψ_E (r) оператора . Так как U (r) > 0, то собственные значения этого оператора образуют непрерывный спектр 0 ≤ E < +∞; Если положить

(4. 26)

то w (Е) dE '= | С (Е) |² dE дает искомую вероятность. Однако мы не можем воспользоваться для вычисления С (Е) функцией ψ (r, t) (4.25), так как она правильна лишь для не очень больших r. Поэтому мы изберем обходный путь, именно, будем считать, что ψ(г, t) имеет корректное поведение в бесконечности, а начальная функций ψ (г, 0) отлична от нуля заметным образом лишь внутри барьера, так что вид функции ψ (г, 0) соответствует тому факту, что при t = 0 частица находится во внутренней области барьера. Определим амплитуду a (t)-, с которой представлено состояние ψ (r, 0) в состоянии ψ (r, t). Имеем

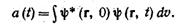(4. 27)

Подставляя сюда ψ (r, t) и ψ* (г, 0) из (4.26) и пользуясь ортогональностью функций ψе (r), найдем

(4.28)

Величина Р (t) = | a (t) |² дает, очевидно, закон распада состояния ψ{г, 0). Как видно, форма этого закона определяется распределением энергии ω (Е) dE в начальном состоянии.

Вернемся теперь к нашей задаче. Выберем ψ (г, 0) так, чтобы ψ (г, 0) = ψ (г) внутри барьера и ψ (г, 0) = 0 вне его. Подставляя теперь ψ (г, t) из (4.25) в (4.27), мы можем игнорировать возрастание ψ ₀ (г) вне барьера, так как там ψ (r, 0) = 0. В силу совпа­дения ψ (r, 0) и ψ (r) внутри барьера и считая, что ψ (г, 0) нор­мировано к 1, получим

(4.29)

На основании (4.28), теперь нетрудно убедиться, что w {E) dE должно быть равно

 

(4.30)

т. е. мы получаем дисперсионную формулу для распределения энергии. Величину называют шириной квазистационарно го уровня E₀. Если через τ = 1/λ обозначить сред­нюю продолжительность жизни частицы в состоянии ψ (г, 0) = ψ₀ (г), то мы получаем

(4.31)

 

— соотношение между шириной квазистационарного уровня и дли­тельностью жизни частицы на этом уровне.

§ 5. Теория радиоактивного α – распада

 

Известно, что многие радиоактивные элементы распадаются, испуская α - частицы. По вылете из атомного ядра α - частица, имея двукратный положительный заряд (+ 2е), ускоряется в кулоновском поле атомного ядра, заряд которого обозначим через Ze (под Z будем подразумевать номер элемента после вылета α - частица, Z = Z' — 2, если Z' есть номер элемента до радиоактивного распада).

Большая прочность α - частицы позволяет предполагать, что она существует в ядре в виде самостоятельного объекта, являясь одним из простых образований, из которых строится атомное ядро. Ясно, что α - частицы может длительно находиться в атомном ядре лишь в том случае, если область вблизи атомного ядра является минимумом потенциальной энергии α - частицы. Кулоновская потен­циальная энергия α - частицы, равная 2Ze²/r, где r — расстояние от ядра до частицы, по мере приближения к ядру, как это изоб­ражено на рис. 5.1 пунктирной кривой, все время возрастает монотонно. Поэтому минимум энергии вблизи ядра может полу­читься лишь в том случае, если на близких расстояниях на α - частицы действуют какие-то иные силы, помимо электрических. Такими силами являются ядерные силы, действующие между нук­лонами. Эти силы весьма велики и действуют лишь на очень малых расстояниях. Именно этими силами и обусловливается смена кулоновского отталкивания на резкое притяжение вблизи ядра, изображенное на рис. 5. 1 сплошной кривой. Такое поведение по­тенциала называют образованием потенциальной ямы или, кратера. При наличии таких сил α - частицы, находящаяся в области r < r₀, т. е. в поле сил притяжения, будет дли­тельно удерживаться внутри ядра.

 

 

Рис. 5. 1. Кривая потенциальной энергии α – частицы в функции расстояния от ядра (r, U_m, r^'). Та же кривая схематизирована (r, U_m, r₀) (резкое падение после r₀).

 

Как же происходит α - распад? Долгое время это оставалось загадкой. Еще Кельвин предполагал, что частицы, испускаемые радиоактивным элементом, как бы кипят внутри потенциального кратера. Время от времени одна из частиц получает избыток - энергии над средней, преодолевает барьер и, вылетев за него, ускоряется отталкивательным по­лем, приобретая большую энергию.

Однако эта наглядная картина, как было показано Резерфордом, противоречит опыту. Резерфорд бомбардировал атомы радиоактивного урана α -частицами тория С'. Энергия α -частиц тория С' равна 13 · 10 ^-6 эрг. Такие частицы, преодолевая кулоновское отталкивание, могут весьма близко подойти к ядру. Оценим расстояния наибольшего сближения r₁.Очевидно, что r₁есть то расстояние, при котором потенциальная энергия частицы 2Z'e²/r₁ будет равна исходной кинетической, т.е. 2Z'e²/r₁ = 13· 10 ^-6 эрг,: Z' есть номер урана и равен 92.. Поэтому мы находим, что r₁= 3-10-¹²см.

Наблюдение показывает, что рассеяние таких частиц строго такое, каким оно должно быть при действии на α - частицы кулоновского поля. Это означает, что ядерные силы начинают дей­ствовать на α - частицы расстояниях меньших, нежели 3 · 10 ^-12 см. Поэтому α -частицы, заключенные в ядре, находятся внутри области, радиус которой меньше 3 • 10^-12 см.

С другой стороны, уран сам является радиоактивным элементом и испускает α -частицы. Измерение энергии этих частиц показы­вает, что она равна 6,6 · 10^-6 эрг.

Эти α -частицы вылетают из ядра, т. е. с расстояний, меньших 3 · 1О^-12 см. Тогда, ускоряясь в кулоновском поле, они должны были бы приобрести энергию, равную высоте потенциального барьера (см. рис. 5. 1) и во всяком случае большую, нежели,13 · 10 ^-6 эрг. Получается же так, как если бы они вылетали с рас­стояния r = 6 · 10 ^-12 см. Таким образом, опыт приводил с точки зрения классической физики к парадоксальному положению: нужно
было предположить, что кулоновское электрическое поле ядра действует на падающие извне α - частицы, но не действует на вылетающие на ядра, либо считать, что закон сохранения энергии не выполняется при радиоактивном распаде.

Решение этого парадокса вытекает из квантовой механики, при­водящей к возможности туннельного эффекта через потенциальный барьер, разделяющий область притяжения (r < r₀) от области отталкивания (r > г₀).

В самом деле, тогда парадокс полностью решается: частица, находящаяся внутри ядра, может иметь энергию, меньшую, нежели высота барьера, и все же пройти через него. Частица же, про­летающая извне, ввиду малой прозрачности барьера лишь в очень редких случаях будет захватываться ядром (так как время пре­бывания ее около ядра очень - мало). Поэтому рассеяние α - частиц, падающих извне, будет обусловливаться кулоновскими силами, действующими за пределами барьера. Предположенная малая прозрачность барьера, согласуется с тем фактом, что периоды радиоактивного α - распада весьма велики.

Применяя теорию прохождения через потенциальные барьеры, легко облечь изложенную идею в математическую форму и найти выражение для константы радиоактивного распада λ - эта константа определяется следующим образом. Если имею­щееся к моменту времени t число нераспавшихся атомов N, то dN будет равно

(5.1)

Для вычисления константы распада λ мы можем применить кван­товую теорию просачивания частиц через потенциальные барьеры, изложенную в предшествующем параграфе. Согласно этой теории α - частицу внутри ядра следует рассматривать как находящуюся в «квазистационарном» состоянии. Обозначая скорость частицы в этом состоянии через υ_i,-, радиус барьера через r₀ и его коэффициент прозрачности через D, мы получим

(5.2)

Остается вычислить D. Ввиду более сложной формы барьера вместо (4.24) мы получим (см. (1.24))

(5.3)

Из рис. 5.1 следует, что первая точка поворота r^'₁ есть г₀ (радиус ядра), вторая (г₂) определится из условия

(5.4)

Таким образом,

(100.5)

Вводя сюда новую переменную %, мы получаем

(5.5')

и, полагая, наконец, ещеm ξ = cos²u, мы без труда вычислим по­рученный интеграл (5.5')

Воспользуемся тем, что отношение меньше, единицы, и {разложим Uо и sin2 Uо в ряд по степеням (достаточно огра­ничиться двумя первыми членами). Тогда мы получим .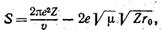

(5.7)

где υ – скорость вдали от ядра, равная . Итак, выражение для константы распада (5.3) раскрывается слёдующим образом:

(5.8)

или

(5.9)

Наиболее замечательным выводом из этой формула является зави­симость между λ и скоростью λ - частицы v. Подобная зависимость еще задолго до квантовой теории этого явления была установлёна на опыте Гайгером и Нэттолом.

Далее мы видим, что 1nλ зависит от номера элемента Z (Z = Z'— 2) и радиуса ядра.

Из опыта известно, что константы распада варьируются в очень |широких пределах: от 10⁶ сек^-1 до 10^-18 сек^-1. Если бы в таких же пределах приходилось варьировать параметры, определяющие λ, то теория была бы наверно неправильной. Замечательным следствием формулы (5.9) является то, что если по эмпирическим данным для λ определять радиусы ядер, то окажется, что они все лежат в тесных границах, примерно от 5 · 10 ^-12 см до 9 · 10^-12 см. Значительное различие в величине λ для разных элементов определяется не различием в радиусах ядер, а различием в энергии вылетающих частиц. Слабую зависимость λ от r₀ и резкую от v следует рассматривать как подтверждение теории.