Расчет температурного поля в стенке цилиндра ДВС

КУРСОВАЯ РАБОТА

По «Теплотехнике»

«ТЕОРЕТИЧЕСКИЕ ЦИКЛЫДВС»

 

 

Вариант №

 

Выполнил студент:

Курсовая работа защищена с оценкой_________________

 

Томск 2009 г.

Содержание

 

Введение……………………………………………………………………......3

 

1. Расчет турбонагнетателя двигателя внутреннего сгорания (ДВС)……4

1.1. Физическая постановка задачи …………………………………..…4

1.2. Решение задачи……………………………………………………….4

2. Расчет теоретического цикла ДВС………………………………………..8

2.1.Физическая постановка задачи………………………………...........8

2.2. Решение задачи.……………………………………………………. 9

1. Расчет водяного радиатора ДВС ………………………………………...15

3.1.Физическая постановка задачи………………………………….....15

3.2.Решение задачи…………………………………………………......16

1. Расчет радиационного теплообмена в ДВС ……………………………19

4.1.Физическая постановка задачи…………………………………….19

4.2.Решение задачи……………………………………………………...19

5. Расчет радиационного теплообмена в ДВС……………………………...21

5.1. Физическая постановка задачи…………………………………....21

5.2. Решение задачи………………………………………………….…21

Заключение ……………………………………………………………….23

Литература………………………………………………………………...24

 

 

 

Введение

 

Целью настоящей курсовой работы по теплотехнике является рассмотрение процессов, связанных с работой двигателей внутреннего сгорания (ДВС). К этим процессам относятся следующие процессы - расчет турбонагнетателя (предварительное сжатие воздуха в поршневом компрессоре); расчет теоретического обратимого замкнутого цикла ДВС (циклы Отто, Дизеля или Тринклера); расчет водяного радиатора (теплообменник, участвующий в системе охлаждения ДВС); расчет температурного поля в стенке цилиндра ДВС (без учета и с учетом отложений на стенке); расчет радиационного теплообмена (вычисление температуры удаляемых газов из рабочего цилиндра ДВС с помощью термопары и оценка погрешности ее измерений за счет теплового излучения). Решение рассматриваемых задач позволит закрепить полученные теоретические знания, разобраться с методикой их решения и приобрести практические навыки, которые могут быть использованы для исследования процессов различных теплотехнических устройств.

 

 

1. Расчет турбонагнетателя двигателя внутреннего сгорания (ДВС).

 

1.1. Физическая постановка задачи.

 

Атмосферный воздух при давлении р₀=0,11 МПа и температуре t₀=5^оС сжимается в турбонагнетателе по политропе с показателем политропы n=1,16._. Степень повышения давления в турбонагнетателе b=p₁/p₀ =1,1. КПД турбонагнетателя h = 0,8. Расход воздуха через турбонагнетатель составляет G₀=1 кг/с.

Определить термические и калорические параметры воздуха перед турбонагнетателем и за ним. Найти работу, техническую работу и теплоту в процессе сжатия.

Вычислить мощность привода турбонагнетателя и сравнить ее с мощностью, необходимой для привода турбонагнетателя при адиабатном и изотермическом сжатии воздуха в нем. Изобразить в масштабе процесс сжатия воздуха в турбонагнетателе в Р-v и Т-s диаграммах.

1.2. Решение задачи.

 

Рабочее тело - воздух (воздух считается двухатомным газом; мольная масса =29 кг/кмоль; изобарная мольная теплоемкость mС_р=29.31 кДж/(кмоль×К); изохорная мольная теплоемкость mС_v=20.93 кДж/(кмоль×К) ([Приложение1]). Газовая постоянная для воздуха R рассчитывается по уравнению

R=R / =8314.4/29=287 Дж/(кг K).

 

Массовые удельные теплоемкости воздуха c_v и c_p определяются как

 

c_v=mс_v/m=20.93/29=0.722 кДж/(кг×К);

 

c_p=mс_р/m=29.31/29=1.01 кДж/(кг×К).

 

T₀ =t₀ +273=5+273 = 278 K.

 

Показатель адиабаты k=c_p/c_v=1.01/0.722=1.4.

 

Находим удельный объём воздуха перед всасыванием его в турбонагнетатель из уравнения состояния

 

v₀=RT₀/p₀=(287×278)/(0.11×10⁶)=0.725 м³/кг,

 

Находим температуру и удельный объём воздуха за турбонагнетателем

 

p1=p₀×b=0.11×1.2=0.132 Мпа.

 

T₁=T₀ b^(n-1)/n=278×1.2^{(1.16-1)/1.16}=284.95 К.

 

v₁=RT₁/p₁=287×284.95/(0.132×10⁶)=0.619 м³/кг.

 

Рассчитываем калорические параметры (u, i, s) в начале и конце сжатия:

а) в начале сжатия:

 

u₀=c_v×T₀=0.722×278=200.716 кДж/кг;

 

i₀=c_p×T₀=1.01×273=275.7 кДж/кг;

 

s₀=c_р×ln(T₀/273)-R×ln(р₀/0.1)=

=1.01×ln(273/273)–0.287×ln((0.12)/0.1)=-0.052 кДж/(кг×К).

 

б) в конце такта сжатия:

u₁=c_v×T₁=0.722×279.07=201.5 кДж/кг;

 

i₁=c_p×T₁=1.01×279.07=281.9 кДж/кг;

 

s₁=c_p×ln(T₁ /273)-R×ln(р₁/0.1)=

=1.01×ln(279.07/273)-0.287×ln(0.132/0.1)=-0.057 кДж/(кг×К).

 

Для вычисления промежуточных значений термодинамических параметров p_п и s_п для заданных значений удельного объема (v_п ) и температуры (T_п), находим давление и энтропию по формулам:

(1)

s_п=c_p×ln(T_п /273)-R×ln(р_п/0.1) (2)

 

Величина давления p_п в промежуточной точке при заданном значении температуры T_п определяется по формуле

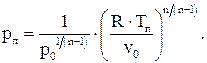(3)

 

Задавая значение v_п=0.63 м³ /кг по формуле (1), определим p_п

 

P_п=0.12(0.653/0.63)^1.3=0.126 МПа

 

 

Составляем таблицу для построения p-v диаграммы

 

Точки (p-v диаграммы)			п
p (МПа)	0.12	0.132	0.126
v (м3 /кг)	0.653	0.607	0.63

 

 

 

 

Результаты расчета процесса сжатия отражены на рабочей (p-v) диаграмме.

Для построения T-s диаграммы в промежуточной точке задаем значение T_п=276 K, затем по формуле (3) определяем p_п и наконец из (2) находим s_п.

p_п=1/(0.12×10⁶)^3.3×((287×276)/0.653)^4.3=0.126 МПа

 

Тогда

 

s_п=1.01×ln(276/273)-0,287×ln(0.126/0.1)=-0.055 KДж/(кг×K).

 

Составляем таблицу для построения T-s диаграммы

 

Точки (T-s диаграммы)			0-1
T (K)		279.07
s (КДж/(кг×K)	-0.052	-0.057	-0.055

 

 

Отведенная теплота:

q_0-1=c_n(T₁–T₀)=c_v[(n-k)/(n-1)]×(T₁–T₀)

 

q_0-1=0.722×(1.3–1.4)/(1.3-1)×(279.07-273)=-1.46 кДж/кг.

 

Работа затраченная на сжатие воздуха

 

l_сж0-1=(R/(n-1))×(Т₀–Т₁)=(0.287/(1.3-1))×(273–279.07)=-5.8 кДж/кг.

 

Располагаемая (техническая) работа:

 

l_расп.0-1=l_сж0-1×n=-5.8×1.3=-7.54 кДж/кг.

 

Правильность расчета: q=l_расп.+Di=-7.54+6.2=-1.34 кДж/кг.

 

Теоретическая и действительная мощности привода турбонагнетателя

 

N_tk=G₀×½l_расп½=0.8×7.54 =6.032 кВт,

 

N_д=N_tk*h=6.032*0.8=4.8256 кВт.

 

Располагаемая (техническая) работа при изотермическом процессе сжатия в компрессоре и теоретическая мощность привода турбонагнетателя:

 

l _.=R×T₀×ln(p₀/p₁)=0.287×273×ln(0.12/0.132)=-7.468кДж/кг;

 

N =G₀×½l _.½=0.8×7.468=5.974 кВт.

 

Располагаемая (техническая) работа при адиабатном процессе сжатия в турбонагнетателе и теоретическая мощность привода турбонагнетателя:

 

l _.=(к×R×Т₀/(к-1))×(1-(p₁/p₀)^(к-1)/к).

l _.=(1.4×0.287×273/(1.4-1))×(1-(0.132/0.12)^(1.4-1)/1.4)=-7.569 кДж/кг

N =G₀×½l _.½=0.8×7.569=6.055 кВт.

 

Сравнивая мощности привода турбонагнетателя при политропном (n=1.3), изотермическом и адиабатном процессах сжатия воздуха видно, что выгодным процессом сжатия является изотермический, однако из-за небольшой поверхности теплообмена и быстроты протекания процесса сжатия осуществить изотермический процесс сжатия воздуха затруднительно, процесс сжатия осуществляется по политропе. Чем больше в процессе отводится теплоты, тем ближе он к изотермическому процессу сжатия воздуха в компрессоре.

Наддув двигателей является одним из наиболее эффективных методов улучшения удельных мощностей и весогабаритных показателей двигателей. Повышение плотности воздуха на впуске в двигатели увеличивает весовое наполнение цилиндров ДВС.

В дизелях повышение плотности воздуха позволяет одновременно увеличивать и подачу топлива. У карбюраторных двигателей увеличивается количество поступающей смеси.

 

 

2. Расчет теоретического цикла ДВС.

 

2.1. Физическая постановка задачи.

 

Воздух с параметрами р₁=0.132 Мпа и Т₁=279 К поступает в двигатель внутреннего сгорания (ДВС), где он является рабочим телом в теоретическом цикле ДВС со смешанным подводом теплоты. Степень сжатия в цикле - e = 18; степень повышения давления - l=1; степень предварительного расширения r=1.5. Массовый расход газа G₀=0,8 кг/с. Относительный внутренний КПД ή_о=0.62; механический КПДή_м =0.7; число цилиндров =4, а тактность ДВС τ_так=2.

Низшая теплота сгорания топлива составляет

Процессы сжатия и расширения газа принять адиабатными.

Определить: термические параметры газа в характерных точках цикла, изменение внутренней энергии, энтальпии, а так же работу, техническую работу и теплоту каждого процесса цикла; работу цикла; подведенную и отведенную в цикле теплоту; среднюю температуру подвода теплоты, среднеиндикаторное давление, термический КПД цикла и сравнить его с термический КПД обратимого цикла Карно для того же интервала температур.

Рассчитать теоретическую, индикаторную, эффективную мощности ДВС, удельный эффективный и часовой расходы топлива.

Вычислить диаметр цилиндра D двигателя, если принять, что ход поршня S_пор равен диаметру цилиндра.

Изобразить теоретический цикл ДВС в Р-V и Т-s диаграммах в масштабе. Показать на диаграммах подведенную и отведенную теплоту цикла, и техническую работу процессов сжатия и расширения.

Найти эффективный удельный b_е, кг/(кВт ч) и часовой В, кг/ч расход топлива.

 

2.2. Решение задачи

 

В соответствие с входными данными в данном варианте рассматривается цикл Дизеля.

Рабочее тело обладает свойствами воздуха

В точке 1 значения термических параметров (p, v, T) и калорических (u, i, s) задаются из первой задачи

р₁=0.132 МПа, v₁=0.607 м³/ кг, Т₁=279.07 К.

Точка 2.

Так как степень сжатия e=v₁/v₂=18, то удельный объем

 

v₂=v₁/e=0.607/18=0.034 м³/кг.

 

Расчет давления р₂.

Из уравнения адиабатного процесса 1-2 рассчитываем давления р2 и, используя уравнения состояния идеального газа, температуру Т₂:

 

р₂=p₁ (v₁/v₂)^к=p₁(e)^к=0.132×18^1,4=7.55 МПа;

 

T₂=(р₂×v₂)/R=(7.55×10⁶×0.034)/287=894.4 К.

 

Точка3.

Процесс 2-3 изобарный процесс, т.е. р₂=р₃=7.55 МПа.

 

Степень предварительного расширения =v₃/v₂=1.5, то

 

v₃=v₂× =0.034×1.5=0.051 м³/кг.

 

Используя уравнения состояния идеального газа находим температуру Т₃:

 

Т₃=(р₃×v₃)/R=(7.55×10⁶×0.051)/287=1341.6 К.

 

Точка 4.

Процесс 4-1 изохорный, т.е. v₄ =v₁=0.607 м³/кг.

Процесс 3–4 адиабатный. Из уравнения адиабатного процесса находим давление р_4.

 

p₄=р₃(v₃/v₄)^k=7.55×(0.051/0.607)^1,4=0.236 МПа.

 

Температура Т₄ находится из уравнения состояния

 

Т₄=(р₄×v₄)/R=(0.236×10⁶×0.607)/287=499.1 К.

 

Для вычисления промежуточных значений термодинамических параметров p_п и s_п для заданных значений удельного объема (v_п) и температуры (T_п), находим давление и энтропию по формулам:

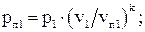(4)

На участке 1-2 задаем v_п1=0.321 м³/кг и по формуле (4) вычисляем р_п1

p_п1=0.132(0.607/0.321)^1.4=0.322 МПа

 

На участке 3-4 задаем v_п2=0,333 м³/кг и вычисляем р_п2

p_п2=p₄(v₄/v_п2)^k=7.55(0.051/0.333)^1.4=0.546 МПа

 

Расчет изменения калорических параметров ( u, i, s).

 

Изменение внутренней энергии производится по формуле, кДж/кг

 

u=c_v× T,

 

u_1-2=u₂-u₁=0.722×(894.4–279.07)=444.27,

 

u_2-3=322.9, u_3-4=-608.3, u_4-1=-158.9

 

Изменение энтальпии производится по формуле, кДж/кг

 

i=c_p× T,

 

i_1-2=i₂-i₁=1,01×(619–268.85)=621.5

 

i_2-3=451.7, i _3-4=-850.9, i_4-1=-222.2

Изменение энтропии производится по формуле, кДж/(кг×К)

 

s=c_p×ln(T_i+1/T_i)-R×ln(p_i+1/p_i).

 

s_1-2=s₂-s₁=0 т.к. процесс 1-2 - адиабатный.

 

s_2-3=0.41, s_3-4=993.591, s_4-1=166.169.

 

Результаты расчета процесса сжатия отражены на рабочей (p-v) диаграмме.

 

Точки (p-v диаграмы)			п1			П2
p (МПа)	0.132	7.55	0.322	7.55	7.55	0.546
v (м3/кг)	0.607	0.034	0.321	0.051	0.607	0.333

 

 

Для построения Т-s диаграммы, найдем значения энтропии в узловых точках (кДж/(кг×K)

s₁=c_p×ln(T₁/273)-R×ln(p₁/0.1)=

=1.01×ln(279.07/273)-0.287×ln(0.132/0.1)=-0.057.

 

Так как процесс 1-2 адиабатный, то s₂=s₁=-0.057.

 

s₃=c_p×ln(T₃/273)-R×ln(p₃/0.1)=

=1.01×ln(1341.6/273)-0.287 ln(7.55/0.1)=0.367.

 

На участке 3-4 s₄=s₃=0.367

 

На участках 2-3, 4-1 для заданных значений температуры, найдем промежуточные значения энтропии.

В изобарном процессе сгорания 2-3 задаем T_п1 = 1000 К; p_п1=p₂=7.55 МПа и

s_п1=c_p×ln(T_п1/273)-R×ln(p_п1/0,1)=

=1,01×ln(1000/273)-0.287×ln(7.55/0.1)=0.07

 

Наконец, в изохорном процессе 4-1 задаем T_п2 = 390 K

p_п2 = p₄ × T_п2/ T₄ = 0.236 × 390/499.1 = 0.184 MПа

 

s_п2= c_р × ln (T_п2/273) – R × ln (p_п2/0.1) =

1.01 × ln (390/273) – 0.287 × ln (0.184/0.1) = 0.185

 

По результатам расчетов построены таблица и T-s диаграмма.

 

Точки (T-s диаграммы)				п1		п2
T (K)	279,07	894,4	1341,6		499,1
s (КДж/(кг×K)	-0,057	-0,057	0,367	0.07	0,367	0.185

 

 

Расчет работы l, располагаемой работы l_p и теплоты q для каждого процесса цикла

Процесс 1 - 2 (адиабатный процесс, dq = 0).

l_1-2 = - u_1-2= -444.27 кДж/ кг; l_р1-2 = - i₁ =-621.5 кДж/ кг; q _1-2= 0.

 

 

Процесс 2 - 3 (изобарный процесс, р₂ = р₃=7,55 МПа).

L_2-3 = р₂×(v₃- v₂) =7,55 ×(0.051-0,034) ×10³= 203,85кДж/ кг;

l_р2-3=0; Q_2-3= i_2-3 = 451,7 кДж/ кг

 

Процесс 3- 4 (адиабатный процесс, dq = 0).

L_3-4 = - u_3-4= 608,3 кДж/ кг; l_р3-4 = - i₁ =850,9 кДж/ кг; q _3-4= 0.

 

Процесс 4 - 1 (изохорный процесс, v₄ = v₁=0,607 м³/кг).

L_4-1 = 0; l_р4-1= v₄×(р₄- р₁)=0,607×(0,236-0,132)×10³ = 63,4 кДж/ кг;

 

Расчет теплоты подведенной и отведенной в цилиндре ДВС.

Подведенная теплота в цикле определяется как сумма поло тельных теплот отдельных процессов цикла. О подводе или отводе теплоты в процессах можно судить так же по изменению энтропии. Если энтропия в процессе увеличивается, то теплота подводиться, если уменьшается, то теплота в процессе отводиться.

В данной задаче теплота подводится в процессе2-3

q₁=q_2-3= 451,7 кДж/ кг.

Отведенная теплота в цикле определяется как сумма отрицательных теплот в отдельных процессах, взятых по модулю

 

q₂ =|q_5-1|= 158,9 кДж/ кг.

 

Работа цикла можно рассчитать как сумму работ всех процессов цикла с учетом их знака, или как сумма располагаемых работ всех процессов цикла с учетом их знака или как разность подведенной и отведенной теплоты цикла

 

l_ц = S li = l_1-2 +l_2-3 + l_3-4 + l_4-1= S l_рi = l_р1-2 +l_р2-3 + l_р3-4 + l_р4-1, l_ц = -621,5 + 0 + 850,9 + 63,4 = 292,8 кДж/ кг,

или l_ц =q₁+q₂= 451,7-158,9=292,8 кДж/ кг.

 

Эффективность работы цикла оценивается термическим КПД, который рассчитывается по уравнению

_t= l_ц / q₁=1- q₂ / q₁; _t= 292,8 /451,7 = 0,648,

или _t=1- =

= 1- =0,648.

 

Термический КПД цикла Карно, работающего в том же интервал температур, что и основной цикл

 

_t^к= 1- Т_мин / Т_мак; _t^к= 1- 279,07 / 1341,6 = 0,792,

 

где Т_мин и Т_мак минимальная и максимальная температура рабочего тела в рассматриваемом цикле.

Теоретическая мощность ДВС составляет, кВт

 

N_t = l_ц×G₀=292,8×0.8 =234,24 кВт

 

Индикаторная мощность, то есть мощность, которую развивают газы внутри цилиндров ДВС, составляет

 

N_0i = N_t× _oi = 234,24 ×0.62 =145,23 кВт

 

Эффективная мощность, то есть мощность, которая снимается с вала двигателя, составляет

 

N_e = N_t× _oi× _м = 234,24 ×0.62 ×0.7 =101,66кВт.

Среднеиндикаторное давление представляет собой такое условно- постоянное давление, которое, действуя на поршень ДВС, в течении одного хода совершает работу равную работе газов за весь цикл

 

p_i=L_i / V_h = l_i /(v₁- v₂) = (l_ц × _oi) /(v₁- v₂);

p_i =(292,8×0.62)/ (0.607 -0.034) ×10³=3,168 ×10⁵ Па.

Часовой расход топлива, кг/ч

 

В= 3600 q₁×G₀×/Q^p_н= 3600× 451,7×0,8 /42000 = 30,97

 

Эффективный удельный расход топлива- это расход топлива на единицу эффективной мощности двигателя

 

b_е=B / N_e= 30,97 / 101,66 = 0.305 кг/ кВт-ч

 

Диаметр цилиндра D (м) определяется из выражения [4]

 

 

 

3. Расчет водяного радиатора ДВС

3.1.Физическая постановка задачи.

По алюминиевым трубкам (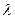 ст=200 Вт/(м.К)) автомобильного радиатора движется вода, циркулирующая в системе охлаждения ДВС. Расход воды через систему охлаждения составляет Gв =1 кг/с, температура воды на входе в трубки радиатора равна t1/ = 90 °С. Трубки в количестве nтр = 152 штук расположены в четыре ряда и омываются поперечно потоком набегающего воздуха с температурой tо =0 °С и скоростью Wж2 =26м/с. Снаружи трубок со стороны воздуха сделано оребрение, Eореб. = 2,4.Определить требуемую высоту трубок, если через стенки цилиндров двигателя передается тепловой поток к охлаждающей воде q=50,6 кВт, который затем отдается в радиаторе воздуху.

 

Характеристика радиатора

 

Внутренний эквивалентный диаметр трубки d=0,00802 м.

Наружный эквивалентный диаметр D=0,0125м.

Толщина стенки трубки ст 0,001м.

Шаг между ребрами S=0,004м.

Толщина ребер р=0,001м.

Высота ребер h=0,006м.

Площадь сечения одной трубки f=7,96·10⁵ м².

Смоченный периметр внутреннего сечения трубки P=0.0397м.

3.2. Решение задачи.

Для теплового расчета водяного радиатора находим теплофизические свойства воды [Приложение 2 ].

Так как температура воды на выходе из радиатора не известна, а теплофизические свойства воды необходимо выбирать по средней температуре охлаждающей жидкости в радиаторе, то предварительно принимаем температуру на выходе из радиатора t1//=80°С. Тогда средняя температура охлаждающей воды составит

tж1= 0,5(t1/+t1//)=0,5(90+80)=85 °С.

По данной температуре (из Приложения 2) находим:

теплоемкость воды С_рж1=4202Дж/(кг×К); плотность _ж1=969кг/м3; теплопроводность _ж1=0,673Вт/(м×К); кинематическая вязкость _ж1 = 0,346×10^-6м²/с; температурный коэффициент объемного расширения 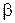_ж1=6,63×10^-4К^-1; число Прандтля Pr_ж1=2,10.

Температура воды на выходе из радиатора

t1//= t1/- Q /(Срж1×G ж1)=90-55138/(4202×1,2)=80 °С.

Рассчитанная температура охлаждающей жидкости на выходе из радиатора совпадает с принятой температурой, то перерасчет средней температуры охлаждающей жидкости не делаем.

Скорость движения охлаждающей жидкости по трубкам

W _ж1= G _ж1/(n_тр× _ж1×f)=1/(152×969×7,96×10^-5 )=0,085м/с.

Находим число Рейнольдса

Re= W_ж1 ×d / _ж1=0,085×0,00802 /0,346×10^-6=1970

и число Грасгофа

Gr_ж1,d=(g 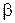_ж1 (t_ж – t_ст)d³)/ _ж1²=

=9,81×6,63×10^-4×(85-45) ×0,00802³/(0,346×10^-6)²=11,21×10⁵.

Здесь предварительно задаем среднюю температуру поверхности трубок tст= 45 0С.

По произведению чисел Gr_ж1,d ×Pr_ж1=11,21×10⁵×2,10=23,5×10⁵ выбираем уравнение подобия и рассчитываем число Нуссельта

Nu_ж1,d= = 0.15Re_ж1,d^0.33 Pr_ж1^0.43 Gr_ж1,d^0,1 (Pr_ж1 /Pr_ст)^0,25 _l=

=0.15×1970^0.33 ×2,1^0.43 ×(11,21×10⁵)^0,1 (2,10 /2,76)^0,25×1=9,489

Рассчитываем коэффициент теплоотдачи от охлаждающей жидкости к стенкам трубок радиатора

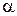₁= Nu_ж1,d× _ж1/d=9,489×0,673/0.00802=796Вт/(м²×К).

Для расчета коэффициента теплоотдачи от стенок трубок радиатора к потоку воздуха находим по средней температуре набегающего потока воздуха t₀=-30 ⁰C его теплофизические свойства [Приложение 2 ]:

теплопроводность _ж2=0,022Вт/(м×К); кинематическая вязкость _ж1=10,80×10^-6м²/с; число ПрандтляPr_ж1=0,723

С учетом выше найденных величин определяем число Рейнольдса

Re= W_ж2 ×D / _ж2=26*0,0125 /10,80×10^-6=30093

и число Нуссельта

Nu_ж2,D= = 0.12Re_ж2,D^0.72 Pr_ж2^0.33 (S /D)^0,4(D/h)^0.14=

 

= 0.15×30093^0.72 0.723^0.33 (0.004 /0.0125)^0,4(0.0125 /0.006)^0,14=158,1.

Коэффициент теплоотдачи от стенок с ребрами водяного радиатора к потоку воздуху

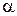₂= Nu_ж2,D× _ж2/D=158,1×0.022/0.0125=278Вт/(м²×К).

Коэффициент теплоотдачи от охлаждающей жидкости к воздуху через оребренную стенку

к= = =344,4Вт/(м²×К)

Рассчитываем среднелогарифмический температурный напор между охлаждающей жидкостью и потоком воздуха.

t=( t_б + t_м) / ln( t_б/ t_м)=

= [(90+30)-(80+30)]/ ln[(90+30)/(80+30)]=115 ⁰C.

Здесь t - среднелогарифмический температурный напор между горячим (охлаждающей жидкостью) и холодным (потоком воздуха) теплоносителями зависит от схемы движения теплоносителей. В данной задаче движения теплоносителей рассматривается как противоток, так как температура потока воздуха при прохождений через радиатор почти не меняется, расход воздуха намного больше, чем расход охлаждающей жидкости протекающей по радиатору (t₂^//=. t₂^/).

Рассчитываем площадь поверхности теплопередачи радиатора

F₁=Q/ (к × t) = 50600/(344,4×115)=1,3м².

Находим высоту трубок радиатора

H =F1/ (nтр×P)=1,3/(0.0397×152) = 0.215м.

Определяем правильность задания температуры стенок водяного радиатора

t_ст = t_ж – Q/(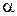 ₁×F₁) =90 – 50600/(718×1,3) = 41 ⁰C.

Найденное значение температуры стенки близко к заданной температуре, поэтому уточнения расчета производить не требуется. При расхождении температур на десятки градусов требуется произвести перерасчет высоты трубок, задав новые значения t_ст.

Характер изменения температур теплоносителей в водяном радиаторе и перепады температур между теплоносителями:

t₁- характер изменения греющего теплоносителя (вода); t₁- характер изменения нагреваемого теплоносителя (воздуха); F_то- поверхность теплообмена; t_Б, t_М -температурные перепады между теплоносителями на входе и выходе из теплообменника

 

 

Расчет температурного поля в стенке цилиндра ДВС

4.1 Физическая постановка задачи

Рассчитать тепловой поток, передаваемый через стенку цилиндра ДВС и температуры поверхностей стенки, толщина которой = 5мм, высота L=150мм, теплопроводность материала 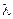=42Вт/(м·град), внутренний диаметр цилиндра D₁=0,508м.

Стенка с одной стороны омывается охлаждающей водой со средней температурой t_ж2=80, коэффициент теплоотдачи ₂=3000Вт/(м² град) с другой стороны омывается раскаленными газами с температурой t_газ=1000 ⁰С и коэффициентом теплоотдачи ₁=200Вт/(м² град).

Во время работы двигателя на наружной поверхности стенки цилиндра образуется накипь толщиной = 4мм, теплопроводность которой λ_н=0,8 Вт/(м град)

Рассчитать температурное поле в стенке, т.е температуры на поверхностях накипи t_c3 , t_c2 и на внутренней стенке цилиндра t_c1, а также температуру газов t_газ при условии, что t_ж2, α_2, α₁ и тепловой поток остаются неизменными.

Изобразить температурное поле в стенке цилиндра ДВС без отложения накипи и с отложением накипи графически в масштабе.

 

4.2 Решение задачи

Для условий задачи определим диаметры D₂ и D₃ .

 

Рассчитываем тепловой поток, передаваемый через стенку цилиндра ДВС по уравнению

Q = (t_газ- t_ж2)× L /(1/( ×D₁)+ ×ln(D₂/D₁)+1/ ( ×D₂))

Q =3,14×(1000-80) ×0,15/(1/(200×0.508)+ ×ln(0.516/0.508) + +1/(3000×0,516))=40593,8 Вт.

Тепловой поток, передаваемый от газа к охлаждающей жидкости, равен тепловому потоку отдаваемому от газа к стенке цилиндра

Q = ×D₁× × (t_ж1- t_с1)× L_,

равен тепловому потоку, передаваемому через стенку цилиндра

 

Q = = (t_с1- t_с2)× L /( ×ln(D₂/D₁))

и равен тепловому потоку, отдаваемому от поверхности стенки цилиндра к охлаждающей воде

Q = 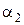×D₂× × (t_с2- t_ж2)× L.

Используя данные уравнения, находим интересующие нас температуры:

температура на поверхности стенки цилиндра со стороны газа

t_с1= t_газ- Q/( ×D₁× × l) = 1000 – 40593,8/(200×0,508×3,14×0,15) = 151,7 ⁰С;

температура на поверхности стенки цилиндра со стороны охлаждающей воды

t_с2= t_ж2 + Q/(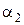 ×D₂× × l) = 80 + 40593,8/(3000×0,516×3,14×0,15) = 135,6 ⁰С_.

Тепловой поток,передаваемый от раскаленного газа к охлаждающей жидкости через стенку цилиндра с отложенной на ней накипью описывается системой уравнении

Q = ×D₁× × (t_газ- t_с1)× L;

Q = = (t_с1- t_с2)× L /( ×ln(D₂/D₁));

Q = = (t_с2- t_с3)× L /( ×ln(D₃/D₂));

Q = 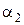×D₃× × (t_с3- t_ж2)× L.

Используя данные уравнения, рассчитываем интересующие нас температуры:

температура на поверхности накипи со стороны охлаждающей воды

t_с3= t_ж2 + Q/(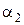 ×D₃× × L) = 80 + 40593,8/(3000×0,524×3,14×0,15) = 134,8 ⁰С:

температура на поверхности между накипью и стенкой цилиндра

t_с2= t_с3 + Q× ln(D₃/D₂)/ (2 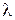_н L) = 134,8 + 40593,8 × ln(0,524/0,516)/ (2×3,14×0,8×0,15) = 963,5 ⁰С;

температура на поверхности стенки цилиндра со стороны газа

t_с1= t_с2+ Q× ln(D₂/D₁)/(2 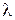L) = 963,5 + 40593,8× ln(0,516/0,508)/ (2×3,14×42×0,15) = 979.5 ⁰С;

температура газа внутри цилиндра при наличии накипи на стенках цилиндра двигателя внутреннего сгорания

t_газ= t_с1 + Q/(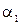 ×D₁× × L) =979,5 +40593,8/(200×0,508×3,14×0,15) = 1827,8 ⁰С

 

 

 

Температурное поле в стенке цилиндра:

а) без отложения накипи; б) с отложением накипи.

Образование накипи на стенках цилиндра вызывает повышение температуры сгорания горючей смеси, что ведет нарушению тепловых процессов протекающих в цилиндре двигателя внутреннего сгорания. Образование накипи на стенках цилиндра двигателя явление нежелательное.