Кроме метода статистических группировок большое значение при изучении взаимосвязи признаков имеет метод корреляционно-регрессионного анализа. Он не только позволяет установить наличие и характер связи, но и дать числовую меру и также направление этой связи.
Корреляционно-регрессионный анализ состоит из нескольких этапов:
1. Экономико-математическое моделирование - отбор факторов, влияющих на результат, выявление направления их влияния и установление формы связи, т.е. корреляционного уравнения (уравнения регрессии). При линейной форме связи уравнение регрессии имеет вид:
Ух = а + b X,
где Ух - теоретический уровень результативного признака (в нашем случае - себестоимость 1 ц зерна);
Х – фактический уровень факторного признака (в нашем случае - урожайность зерновых культур);
a и b - параметры уравнения.
2. Решение корреляционного уравнения - нахождение его параметров. Наиболее распространенный прием нахождения параметров - способ наименьших квадратов (составление и решение системы нормальных уравнений). При линейной форме связи эта система имеет вид:
ΣУ = na + b*ΣХ,
Σ(У*Х) = а*ΣХ + b*ΣХ2,
где: n - численность (объем) совокупности (в нашем случае n = 25).
Коэффициент регрессии («b») показывает, в какой мере в среднем для всей совокупности растет (или снижается) в абсолютном выражении результативный признак при росте факторного признака на единицу (в нашем случае «b» показывает, на сколько руб. растет (или снижается) себестоимость 1 ц зерна при росте урожайности зерновых культур на 1 ц/га).
3. Оценка результатов - определение показателей корреляционного анализа (коэффициентов регрессии, корреляции и детерминации) и надежности этих показателей. При линейной форме связи коэффициент корреляции определяется по формуле:
|
|
,
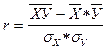где: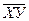 
- средний размер произведения факторного признака на результативный;
, 
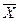- средний размер факторного и результативного признаков;
, 
- средние квадратические отклонения факторного и результативного признаков.
Причем,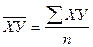 
; 
; 
; 
; 
; 
; 
.
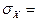
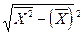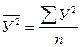Надежность исчисленного коэффициента корреляции определяется отношением его величины к средней ошибке, т.е. по формуле: 
= 
,
где: 
;
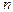- объем совокупности.
Парный коэффициент корреляции может принимать значения от -1 до +1.
Если r - отрицательный, то связь обратная, а если положительный - прямая. Причем если r имеет значение до 0,25 - связь слабая, при r от 0,26 до 0,70 - средняя, при r - более 0,70 - связь сильная.
Возведение в квадрат коэффициента корреляции дает коэффициент детерминации (d = r2), который позволяет сделать вывод, что доля влияния факторного признака на результативный как минимум равна этой величине (d).
Выполнение данного раздела курсовой работы должно осуществляться в следующей последовательности:
1. Составить систему нормальных уравнений и вычислить параметры «b» и «а». Для нахождения параметров уравнения связи и расчета коэффициента корреляции построим вспомогательную таблицу (см. табл. 3).
2. Записать уравнение связи и сделать по нему выводы.
3. Рассчитать по каждой организации ожидаемый (по уравнению регрессии) теоретический уровень результативного признака при фактическом уровне факторного признака и результаты записать в табл. 3.
4. Определить величины для исчисления линейного коэффициента корреляции: - средний размер факторного признака: ;
|
|
- средний размер результативного признака: ;
- среднее произведение размеров признаков: ;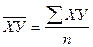
- среднее квадратическое отклонение факторного признака: ;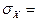
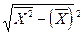- среднее квадратическое отклонение результативного признака: .
Таблица 3
Расчет данных для решения уравнения связи и определения
коэффициента корреляции
| № организации | Урожайность зерновых культур, ц/га (Х) | Себестоимость 1 ц, р. (У) | Х*У | Х2 | У2 | Ух | |
| … | … | … | … | … | … | … | |
| Итого | ∑Х | ∑У | ∑(Х*У) | ∑Х2 | ∑У2 | ∑Ух | |
5. Вычислить линейный коэффициент корреляции (r).
6. Оценить надежность исчисленного коэффициента корреляции.
7. Рассчитать коэффициент детерминации (d).
8. Сделать выводы.