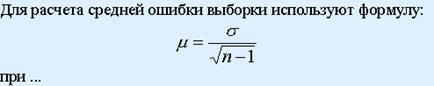
Малой выборке
Cредняя ошибка случайной повторной выборки..., если ее объем увеличить в 4 раза
Уменьшится в 2 раза

t
Средняя ошибка выборки для средней величины характеризует:
Среднюю величину всех возможных расхождений выборочной и генеральной средней
Под выборочным наблюдением понимают:
Несплошное наблюдение части единиц совокупности, отобранных случайным способом
Недостающим элементом в формуле дисперсии доли для генеральной совокупности является 
W
Пропорция отбора в выборочную совокупность при механической выборке определяется:
Соотношением объемов выборочной и генеральной совокупностей
Способ собственно-случайного отбора в выборочную совокупность заключается в отборе из генеральной совокупности:
Без какой либо системности
Необходимая численность серийной выборки при бесповторном отборе определяется по формуле:

Для оценки результатов малой выборки пользуются:
Критерием Стъюдента
Недостающим элементов в формуле предельной ошибки выборки для доли при бесповторном отборе является: 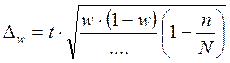
n
Для получения предельной ошибки выборки необходимо умножить среднюю ошибку выборки на:
Коэффициент доверия
По формуле  определяется ошибка выборки:
определяется ошибка выборки:
Средняя бесповторная
При случайном бесповторном отборе средняя ошибка выборки определяется по формуле:

Выборка называется малой, если ее объем составляет менее:
Единиц
Выборка заключающаяся в отборе единиц из общего списка единиц генеральной совокупности через равные интервалы в соответствии с установленным процентом отбора называется:
Механической
Для использования выборочной совокупности для дальнейшего анализа развития социально-экономического явления необходимо, чтобы разница между средним значением генеральной совокупности и средним значением выборочной совокупности была не более ошибки выборки:
Предельной
Между различными явлениями и их признаками выделяют два типа связей:
Функциональная и статистическая
Функциональной называется связь, при которой:
Каждому значению признака-фактора соответствует вполне определенное значение результативного признака
В зависимости от направления действия функциональные и статистические связи могут быть:
Прямые и обратные
По аналитическому выражению функциональные и статистические связи могут быть:
Прямолинейные и криволинейные
Однофакторные и многофакторные
По количеству факторов, действующих на результативный признак статистические связи могут быть:
Однофакторные и многофакторные
Линейный коэффициент корреляции может быть:
Как положительной, так и отрицательной величиной
В линейном уравнении коэффициент регрессии (а) показывает:
На сколько в среднем изменится «у» при изменении «х» на одну единицу
С помощью корреляционного анализа можно:
Измерить тесноту связи между варьирующими признаками
С помощью регрессионного анализа можно: