ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ ОБЬЕКТОВ ПРИ РАЗЛИЧНЫХ ВИДАХ ИСПЫТАНИЙ

 

Вариант №4

 

 

Выполнил: Костин А.А

Группа: АМС-41

Шифр зачетки: 71611

Проверил:

Профессор Новоселов В.Г.

 

Екатеринбург

 

Задача 1. Оценить нижнюю Рн и верхнюю Рв доверительные границы при доверительной вероятности 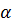, если число испытываемых изделий составляет n и при определительных испытаниях произошло m отказов.

 

Исходные данные по вариантам

 

Вариант
а	0,95	0,94	0,93	0,92	0,91	0,9	0,92	0,94	0,95	0,96
n
m

 

Решение проводится в следующей последовательности.

1. Определяется частость сохранения работоспособности по формуле

 

=

 

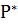Р^*=120-20/120=0,83

2. Проверяются два условия, при которых используется нормальное распределение

 

n 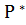>10 и n (1– 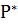) >10

120*0,83=99,6>10 и 120(1-0,83)=20,4>10

 

3. При Р(t) = 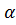по таблице 1 определяют методом экстраполирования результатов на соответствующем интервале Uр = U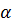

Uр = U 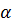=1,4

 

4. Определяют среднее квадратическое отклонение Snx по формуле

 

Snx =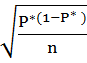

 

S_nx= 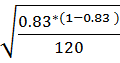= =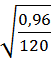0,089

5. Нижнюю и верхнюю доверительные границы определяют по формулам

 

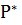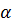Рн = + U Snx=0,83-1,4*0,089=0,705

 

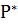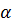Рв = – U Snx=0,83+1,4*0,089=0,954

 

 

Задача 2. Определить требуемый объём выборки n, если частость сохранения работоспособности равна 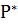, заданы доверительный интервал d и односторонняя доверительная вероятность 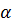. Предполагается применимость нормального распределения.

 

Исходные данные по вариантам

 

Вариант
Р*	0,8	0,75	0,71	0,81	0,83	0,79	0,75	0,86	0,88	0,7
а	0,95	0,94	0,93	0,92	0,91	0,9	0,92	0,94	0,95	0,96
Рв	0,866	0,813	0,766	0,854	0,875	0,834	0,798	0,905	0,923	0,781
Рн	0,733	0,687	0,654	0,766	0,785	0,746	0,702	0,815	0,837	0,619

 

Решение проводится в следующей последовательности.

1. При вероятности безотказной работы Р(t) = 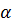=0,91 по таблице 1 методом экстраполирования результатов на соответствующем интервале определяют Uр = U 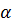=-1,4

2. Определяют доверительный интервал d по формуле

 

d = Р_в – Р_н

 

d=0,875-0,785=0,09

из формулы:

 

n = ;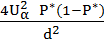

 

n=4(-1,4)²*0,83*(1-0,83)/0,09²=136,5=137

 

 

задача 3. Испытано три изделия, каждое в течение 600 ч. В процессе испытаний получено m отказов. После отказов работоспособность изделий восстанавливали. Требуется определить нижнюю границу средней наработки на отказ Тн с односторонней доверительной вероятностью .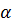

Исходные данные по вариантам.

Вариант
m
a	0,7	0,8	0,9	0,95	0,7	0,8	0,9	0,95	0,9	0,95

 

Решение проводится в следующей последовательности.

 

1. Определяется суммарное время испытаний n изделий, ч:

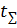= n · t = 3 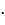600 = 1800 ч.

2. По таблице 2 в зависимости от числа отказов m и доверительной вероятности 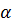находится значение параметра 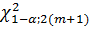=11,8

3. Нижняя граница средней наработки на отказ определяется по формуле

Тн =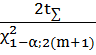

Т_н=2*1800/11,8=305 ч.

 

Задача 4. Определить число n изделий, необходимое для испытаний при условии, что отказов при испытании не возникает, т.е. m = 0, если задано, что нижняя доверительная граница составляет Рн, а доверительная вероятность .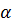

Исходные данные по вариантам.

Вариант
a	0,7	0,8	0,9	0,95	0,7	0,8	0,9	0,95	0,9	0,95
Рн	0,9	0,95	0,99	0,9	0,95	0,9	0,9	0,95	0,95	0,99

 

Для подтверждения значения Рн с доверительной вероятностью 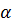необходимо испытать

n =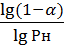

n=lg(1-0.7)/lg0.95=-1,2/-0,051=23,5=24

 

задача5. Определить суммарную длительность испытаний 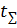для подтверждения нижней границы Тн средней наработки на отказ. Доверительная вероятность составляет 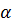, число отказов принимается

m = 0.

Исходные данные по вариантам.

Вариант
Тн, ч
a	0,7	0,8	0,9	0,8	0,7	0,8	0,9	0,7	0,7	0,8

 

Решение производится в следующей последовательности.

1. При заданных значениях m = 0 и доверительной вероятности 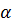по таблице 2 находят значения параметра 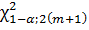=2,41

2. Длительность испытаний определяют по формуле

 

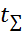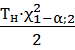= =(200*2,41)/2=241 ч.

 

Задача 6. Требуется оценить по результатам испытаний изделия нижнюю доверительную границу Рн за время t при доверительной вероятности

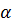= 0,8. Время испытаний составляет t_и = кt, число испытываемых изделий n, число отказов m. Отказы по времени распределены логарифмически нормально с средним квадратическим отклонением .

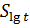Исходные данные по вариантам.

Вариант
к
n
m
Slgt	0,3	0,32	0,34	0,3	0,32	0,3	0,3	0,32	0,3	0,32

 

Решение производится в следующей последовательности.

1. Определяется частость сохранения работоспособности по формуле

 

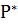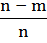= =17-1/17=0,94

2. Определяется нижняя доверительная граница Рни на время tn по формуле

Р_ни = 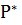+ U 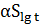=0,94-0,842*0,32=0,671

где U 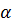- квантиль нормального распределения, соответствующая доверительной вероятности 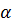(по таблице 1 при 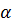= 0,8 квантиль

U 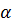= - 0,842).

3. По найденному значению Рни по таблице 1 определяют квантиль Uри=-0.44_.

4. Для пересчёта вероятностных оценок с времени испытаний t_и на заданный ресурс t определяют квантиль Uр по формуле

 

U_p = 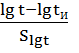+ U_ри= 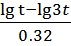+(-0.44)=-1.09-0.44=-1,53 Я же Вам даже посчитал -0,478, что вы чудите?!

5. По найденному значению Up по таблице 1 определяют нижнюю доверительную границу Рн =0.9345

6. Для подтверждения найденного значения Рн следовало бы испытать n_и изделий

 

n_и = 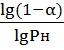=lg(1-0.8)/lg0.9345=-1.609/(-0,06)=26,8

 

 

7. n_к = 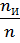=26,8/17=1,5=2

q = 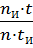=26,8t/17*3t=0,5=1