Федеральное государственное образовательное бюджетное учреждение
Высшего образования
«ФИНАН
«ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ
РОССИЙСКОЙ ФЕДЕРАЦИИ»
Департамент анализа данных, принятия решений и финансовых технологий
О.А.Баюк, С.Я.Криволапов, Т.Л. Мелехина
Нахождение глобальных экстремумов функций (Excel)
Учебно-методические рекомендации для проведения
семинара №11 по компьютерному практикуму
Для бакалавров направления 38.03.01 «Экономика»
Электронное издание
Москва 2017
Нахождение глобальных экстремумов функций (Excel)
Введение
Локальным экстремумом называют точку пространства исследования, в которой функция имеет наибольшее (наименьшее) значение по сравнению с ее значениями во всех других точках ближайшей окрестности. Часть пространства исследования может содержать много локальных экстремумов и следует сохранять осторожность, чтобы не принять первый из них за решение задачи.
Глобальным экстремумом будем называть точку пространства исследования, в которой функция имеет большее (меньшее) значение по сравнению с любой другой точкой пространства исследования. Таким образом, глобальный экстремум – это оптимальное решение для всего пространства исследования.
Задачу для функции одной переменной можно поставить следующим образом. Пусть значения переменной x заключены в интервале [ a; b ]. Интервал значений переменной x, в котором производится поиск оптимума целевой функции, будем называть интервалом неопределенности. В начале процесса оптимизации этот интервал имеет длину b-a. Необходимо определить значения оптимума функции с погрешностью 
, то есть найти в интервале [ a; b ] точку x, такую что
|
|
– при поиске максимума, или
– при поиске минимума.
Таким образом, нам необходимо иметь план действий, неизбежно приводящий к определениюточки x* с точностью , где бы эта точка не лежала в области поиска. Рассматриваемые в дальнейшем методы и являются такими планами действий по поиску оптимумов функций.
Очевидно, наиболее естественным и простым способом сужения интервала неопределенности для одномерной функции является его деление на несколько равных частей с последующим вычислением значений функции в узлах полученной сетки.
Выполнение работы.
Задача.
Поискглобального экстремума функции 
Найти глобальный максимум функции
Решение:
Построим на листе Excel график функции. Для этого в диапазоне В7:В107 располагаем значения независимой переменной, в диапазоне С7:С107 вычисляем соответствующие значения функции
Рис. 2.1.1. Визуальное определение глобального экстремума.
Анализируя график, замечаем, что глобальный максимум расположен в окрестности точки x =1.5. Для более точного определения точки глобального максимума в диапазоне В7:В107 вставляем между 1.5 и 1.6 значения 1.51, 1.52, …, 1.59. В диапазоне С7:С107 вычисляем соответствующие значения функции. Определяем, что производная обращается в ноль между значениями 1.543 и 1.544 (см. Рис. 2.1.2.) Поступая аналогичным образом необходимое количество раз, можно получить значение точки экстремума с заданной точностью. Указанный процесс последовательных приближений отражен на рисунках с 2.1.2. по 2.1.9. В результате получено значение точки глобального экстремума х0=1.54000594190.
|
|
Рис. 2.1.2. Уточнение значения точки глобального экстремума
(
).
Рис. 2.1.3. Уточнение значения точки глобального экстремума
(
).
Рис. 2.1.4. Уточнение значения точки глобального экстремума
(
).
Рис. 2.1.5. Уточнение значения точки глобального экстремума
(
).
Рис. 2.1.6. Уточнение значения точки глобального экстремума
(
).
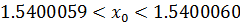Рис. 2.1.7. Уточнение значения точки глобального экстремума (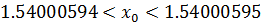
).
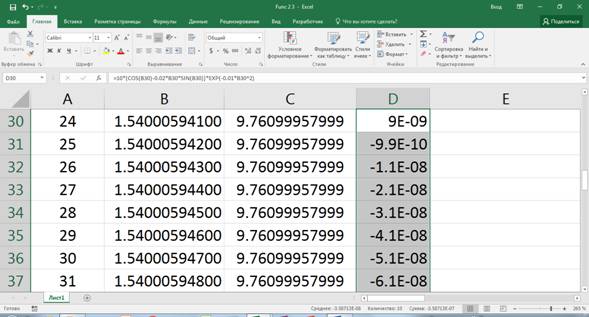
Рис. 2.1.8. Уточнение значения точки глобального экстремума (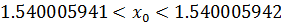
).
Рис. 2.1.9. Значение корня х=1.54000594190.
Причем, при решении данного примера можно использовать как точные значения производной, которые вычисляются по формуле
,
так и приближенные, вычисленные по формуле
где 
.
Еще один способ решения данной задачи основан на использовании решения уравнения методом касательных.
Поскольку ,
Уравнение 
эквивалентно уравнению
В качестве начального приближения корня этого уравнения можно взять
(это значение можно получить из графика, приведенного на рисунке 2.1.1.)
Пусть 
Подробное описание алгоритма решения уравнения методом касательных приведено в пособии для семинара № 8. Результаты работы алгоритма приведены в таблице 2.1.
Таблица 2.1.
| Поиск корня f'(x)=0 | методом касательных | |||
| Xk |  (Xk)
|  (Xk)
| Xk+1 | dXk |
| 1.50000000000 | 0.0408123520696 | -1.019567002 | 1.540029103 | 0.040029103 |
| 1.54002910252 | -0.0000236346008 | -1.02046476 | 1.540005942 | -2.31606E-05 |
| 1.54000594190 | -0.0000000000003 | -1.020464731 | 1.540005942 | -3.193E-13 |
| 1.54000594190 | 0.0000000000001 | 1657.377773 | 1.540005942 |
Из таблицы видно, что значение корня с машинной точностью получено за три итерации.
|
|
Задания для самостоятельной работы.
Задача 1.
Найти глобальный экстремум функции:
Задача 2.
Найти глобальный экстремум функции:
