Решение задач с поразрядными операциями

Для решения этих задач удобно применять метод, предложенный А.В. Здвижковой (г. Армавир) и обоснованный автором[2]. Введём обозначения

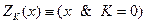
Это означает, что если истинно , то это равносильно тому, что истинно 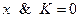. Для сокращения записи вместо будем писать просто .

Пусть в двоичной записи числа K бит с номером i, обозначаемый как k_i, равен 1. Если при этом для некоторого x выполнено условие , то соответствующий i -й бит в двоичной записи числа x равен нулю, так как должно выполняться условие .

Для преобразования выражений полезно следующее свойство:

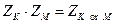
где «or » означает поразрядную дизъюнкцию между двумя натуральными числами. Для доказательства предположим, что в двоичной записи числа K биты с номерами i ₁, i ₂, …, i_q равны 1, а остальные равны 0; а в двоичной записи числа M биты с номерами j ₁, j ₂, …, j_p равны 1, а остальные равны 0. Истинность выражения в левой части означает, что все биты числа x, входящие во множества B_K = { i ₁, i ₂, …, i_q } и B_M = { j ₁, j ₂, …, j_p } одновременно равны нулю. Поэтому любая комбинация битов из этих множеств тоже равна нулю. Это справедливо, в том числе, и для множества, которое представляет собой объединение множеств B_K и B_M, то есть, для множества единичных битов числа K or M.

Самый важный результат можно сформулировать так:

Условие истинно для любых натуральных значений x тогда и только тогда, когда все единичные биты двоичной записи числа M входят во множество единичных битов двоичной записи числа K.

Доказательство. Пусть в двоичной записи числа K биты с номерами i ₁, i ₂, …, i_q равны 1, а остальные равны 0. Пусть также истинно для некоторого x, это значит, что в числе x биты с теми же номерами – нулевые. Если все единичные биты двоичной записи числа M входят во множество B_K = { i ₁, i ₂, …, i_q }, то истинно и высказывание , а следовательно – высказывание (1 ® 1 = 1). Если же хотя бы один бит двоичной записи числа M не входит во множество B_K (пусть это будет бит с номером j), то для тех х, у которых все биты из множества B_K нулевые, а бит j равен 1, выполняется , но не выполняется , так что высказывание ложно.

Для упрощения выражений полезен следующий результат:

Условие при любых натуральных K, M и N ложно для некоторых натуральных значений x.

Идея доказательства состоит в том, чтобы представить импликацию в виде произведения двух импликаций:

.

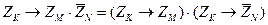Вторая импликация в правой части ложна хотя бы для некоторых x, поскольку из того, что некоторые биты числа x равны нулю (выполняется ) совершенно не следует, что какие-то другие (или те же самые) биты того же числа ненулевые (выполняется ). Строгое доказательство дано в статье, ссылка на которую приведена в сноске на предыдущей странице.

Метод, предложенный А.В. Здвижковой заключается в следующем:

1) упростить заданное выражение, сведя его к импликации, в которой нет инверсий

2) применить полученные выше результаты для нахождения всех подходящих значений неизвестного числа a, включая минимальное и максимальное значения.

Этот же метод можно применить и в том случае, когда результат поразрядной операции «И» сравнивается не с нулём, а с другими числами. Например, рассмотрим выражение R = (x &125= 5). Переведём числа в двоичную систему:

6 5 4 3 2 1 0

125 = 1111101₂

5 = 101₂.

Истинность R означает, что

1) биты числа x с номерами 3, 4, 5 и 6 равны 0;

2) биты числа x с номерами 0 и 2 равны 1.

С учётом введённых выше обозначений можно записать эквивалентное условие:

R = (x &125= 5) Û .

Применяя операцию «НЕ» к этому выражению, получаем

= (x &125¹ 5) Û Û .

В общем виде для чисел b и c, таких, что множество единичных битов числа c входит во множество единичных битов числа b, имеем

R = (x & b = c) Û

= (x & b ¹ c) Û .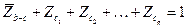

где c­ ₁, c­ ₂, …, c­_q – степени числа 2, которые соответствуют единичным битам числа c. Например, для
c = 5 = 101₂ имеем c­ ₁ = 2² = 4, c­ ₂ = 2⁰ = 1.

Задачи для тренировки:

1) Для какого из указанных значений числа X истинно высказывание

((X < 5)→(X < 3)) Ù ((X < 2)→(X < 1))

1) 1 2) 2 3) 3 4) 4

2) Для какого числа X истинно высказывание ((X > 3)Ú(X < 3)) →(X < 1)

1) 1 2) 2 3) 3 4) 4

3) Для какого числа X истинно высказывание X > 1 Ù ((X < 5)→(X < 3))

1) 1 2) 2 3) 3 4) 4

4) Для какого имени истинно высказывание:

(Первая буква имени гласная → Четвертая буква имени согласная)?

1) ЕЛЕНА 2) ВАДИМ 3) АНТОН 4) ФЕДОР

5) Для какого символьного выражения неверно высказывание:

Первая буква гласная → (Третья буква согласная)?

1)abedc 2)becde 3) babas 4) abcab

6) Для какого числа X истинно высказывание (X > 2)Ú(X > 5)→(X < 3)

1) 5 2) 2 3) 3 4) 4

7) Для какого из значений числа Z высказывание ((Z > 2)Ú(Z > 4)) →(Z > 3) будет ложным?

1) 1 2) 2 3) 3 4) 4

8) Для какого имени истинно высказывание:

(Первая буква имени согласная → Третья буква имени гласная)?

1) ЮЛИЯ 2) ПЕТР 3) АЛЕКСЕЙ 4) КСЕНИЯ

9) Для какого из значений числа Y высказывание (Y < 5) Ù ((Y > 1) → (Y > 5)) будет истинным?

1) 1 2) 2 3) 3 4) 4

10) Для какого символьного выражения верно высказывание:

(Первая буква согласная) Ù (Вторая буква гласная)?

1) abcde 2) bcade 3) babas 4) cabab

11) Для какого имени истинно высказывание:

(Вторая буква гласная → Первая буква гласная) Ù Последняя буква согласная?

1) ИРИНА 2) МАКСИМ 3) МАРИЯ 4) СТЕПАН

12) Для какого имени истинно высказывание:

(Первая буква согласная → Последняя буква гласная) Ù Вторая буква согласная?

1) ИРИНА 2) СТЕПАН 3) МАРИНА 4) ИВАН

13) Для какого имени истинно высказывание:

(Первая буква согласная → Вторая буква согласная) Ù Последняя буква гласная?

1) КСЕНИЯ 2) МАКСИМ 3) МАРИЯ 4) СТЕПАН

14) Для какого имени истинно высказывание:

(Вторая буква гласная → Первая буква гласная) Ù Последняя буква согласная?

1) ИРИНА 2) МАКСИМ 3) МАРИЯ 4) СТЕПАН

15) Для какого имени истинно высказывание:

(Первая буква согласная → Последняя буква согласная) Ù Вторая буква согласная?

1) ИРИНА 2) СТЕПАН 3) МАРИЯ 4) КСЕНИЯ

16) Для какого имени истинно высказывание:

(Первая буква гласная → Вторая буква гласная) Ù Последняя буква гласная?

1) ИРИНА 2) МАКСИМ 3) АРТЕМ 4) МАРИЯ

17) Для какого названия животного ложно высказывание:

Заканчивается на согласную Ù В слове 7 букв→ (Третья буква согласная)?

1) Верблюд 2) Страус 3) Кенгуру 4) Леопард

18) Для какого названия животного ложно высказывание:

В слове 4 гласных буквы Ù (Пятая буква гласная) Ú В слове 5 согласных букв?

1) Шиншилла 2) Кенгуру 3) Антилопа 4) Крокодил

19) Для какого названия животного ложно высказывание:

Четвертая буква гласная → (Вторая буква согласная)?

1) Собака 2) Жираф 3) Верблюд 4) Страус

20) Для какого слова ложно высказывание:

Первая буква слова согласная → (Вторая буква имени гласная Ù Последняя буква слова согласная)?

1) ЖАРА 2) ОРДА 3) ОГОРОД 4) ПАРАД

21) Для какого числа X истинно высказывание (X×(X-16) > -64) →(X > 8 )

1) 5 2) 6 3) 7 4) 8

22) Для какого числа X истинно высказывание (X×(X-8) > -25 + 2×X) →(X > 7 )

1) 4 2) 5 3) 6 4) 7

23) Для какого символьного набора истинно высказывание:

Вторая буква согласная Ù (В слове 3 гласных буквы Ú Первая буква согласная)?

1) УББОШТ 2) ТУИОШШ 3) ШУБВОИ 4) ИТТРАО

24) Для какого имени ложно высказывание:

(Первая буква гласная Ù Последняя буква согласная)→ (Третья буква согласная)?

1) ДМИТРИЙ 2) АНТОН 3) ЕКАТЕРИНА 4) АНАТОЛИЙ

25) Для какого имени истинно высказывание:

Первая буква гласная Ù Четвертая буква согласная Ú В слове четыре буквы?

1) Сергей 2) Вадим 3) Антон 4) Илья

26) Для какого числа X истинно высказывание
((X < 4) →(X < 3)) Ù ((X < 3) →(X < 1))

1) 1 2) 2 3) 3 4) 4

27) Для какого имени истинно высказывание:

(Первая буква согласная → Вторая буква согласная) Ù Последняя буква согласная?

1) ИРИНА 2) МАКСИМ 3) СТЕПАН 4) МАРИЯ

28) Для какого имени истинно высказывание:

(Первая буква согласная → Последняя буква согласная) Ù Вторая буква согласная?

1) ИРИНА 2) СТЕПАН 3) КСЕНИЯ 4) МАРИЯ

29) Для какого имени истинно высказывание:

(Первая буква согласная → Вторая буква согласная) Ù Последняя буква гласная?

1) КСЕНИЯ 2) МАКСИМ 3) СТЕПАН 4) МАРИЯ

30) Для какого имени истинно высказывание:

(Последняя буква гласная → Первая буква согласная) Ù Вторая буква согласная?

1) ИРИНА 2) АРТЁМ 3) СТЕПАН 4) МАРИЯ

31) Для какого слова истинно высказывание:

(Первая буква согласная → (Вторая буква согласная Ú Последняя буква гласная))?

1) ГОРЕ 2) ПРИВЕТ 3) КРЕСЛО 4) ЗАКОН

32) Для какого имени истинно высказывание:

(Первая буква согласная → Вторая буква гласная) Ù Последняя буква согласная?

1) АЛИСА 2) МАКСИМ 3) СТЕПАН 4) ЕЛЕНА

33) Для какого имени истинно высказывание:

(Вторая буква гласная → Первая буква гласная) Ù Последняя буква согласная?

1) АЛИСА 2) МАКСИМ 3) СТЕПАН 4) ЕЛЕНА

34) Для какого названия реки ложно высказывание:

(Вторая буква гласная → Предпоследняя буква согласная) Ù Первая буква стоит в
алфавите раньше третьей?

1) ДУНАЙ 2) МОСКВА 3) ДВИНА 4) ВОЛГА

35) Для каких значений X и Y истинно высказывание:

(Y+1 > X) Ú (Y+X < 0) Ù (X > 1)?

1) X = 0,5; Y = -1,1 2) X = 1,1; Y = -4
3) X = -1; Y = -4 4) X = -1/10; Y = -1,1

36) Для какого слова истинно высказывание:

(Вторая буква согласная Ú Последняя буква гласная) → Первая буква гласная?

1) ГОРЕ 2) ПРИВЕТ 3) КРЕСЛО 4) ЗАКОН

37) Для какого имени истинно высказывание:

Первая буква согласная Ù (Вторая буква согласная → Четвертая буква гласная)?

1) ИВАН 2) ПЕТР 3) ПАВЕЛ 4) ЕЛЕНА

38) Для какого названия станции метро истинно высказывание:

(Первая буква согласная → Вторая буква согласная) ~ Название содержит букву «л»)?

Знаком ~ обозначается операция эквивалентности (результат X ~ Y – истина, если значения X и Y совпадают).

1) Маяковская 2) Отрадное 3) Волжская 4) Комсомольская

39) Для какого названия города истинно высказывание:

(Первая буква гласная Ù Последняя буква гласная) ~ Название содержит букву «м»?

Знаком ~ обозначается операция эквивалентности (результат X ~ Y – истина, если значения X и Y совпадают).

1) Москва 2) Дюссельдорф 3) Амстердам 4) Атланта

40) Для какого имени истинно высказывание:

(Первая буква согласная Ú Вторая буква гласная) → В слове 4 буквы?

1) МИХАИЛ 2) ГРИГОРИЙ 3) ЕВГЕНИЙ 4) ИОЛАНТА

41) Для какого числа X истинно высказывание ((X < 5) → (X < 3))Ù ((X < 2) → (X > 1))

1) 1 2) 2 3) 3 4) 4

42) На числовой прямой даны два отрезка: P = [5, 15] и Q = [12, 18]. Выберите такой отрезок A, что формула

((x Î А) → (x Î P)) \/ (x Î Q)

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) [3, 11] 2) [2, 21] 3) [10, 17] 4)[15, 20]

43) На числовой прямой даны два отрезка: P = [5, 10] и Q = [15, 18]. Выберите такой отрезок A, что формула

((x Î А) → (x Î P)) \/ (x Î Q)

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) [3, 11] 2) [6, 10] 3) [8, 16] 4)[17, 23]

44) На числовой прямой даны два отрезка: P = [25, 30] и Q = [15, 20]. Выберите такой отрезок A, что формула

((x Î А) → (x Î P)) \/ (x Î Q)

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) [10, 15] 2) [12, 30] 3) [20, 25] 4)[26, 28]

45) На числовой прямой даны два отрезка: P = [2, 20] и Q = [15, 30]. Выберите такой отрезок A, что формула

((x Ï А) → (x Ï P)) \/ (x Î Q)

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) [0, 15] 2) [3, 20] 3) [10, 25] 4)[25, 40]

46) На числовой прямой даны два отрезка: P = [10, 25] и Q = [0, 12]. Выберите такой отрезок A, что формула

((x Ï А) → (x Ï P)) \/ (x Î Q)

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) [10, 15] 2) [20, 35] 3) [5, 20] 4)[12, 40]

47) На числовой прямой даны два отрезка: P = [10, 20] и Q = [12, 15]. Выберите такой отрезок A, что формула

((x Ï А) → (x Ï P)) \/ (x Î Q)

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) [10, 15] 2) [20, 35] 3) [5, 20] 4)[12, 40]

48) На числовой прямой даны два отрезка: P = [10, 20] и Q = [5, 15]. Выберите такой отрезок A, что формула

((x Î P) → (x Î Q)) \/ (x Î A)

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) [10, 15] 2) [20, 35] 3) [15, 22] 4)[12, 18]

49) На числовой прямой даны два отрезка: P = [10, 20] и Q = [15, 25]. Выберите такой отрезок A, что формула

((x Î P) → (x Î Q)) \/ (x Î A)

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) [8, 17] 2) [10, 12] 3) [15, 22] 4)[12, 18]

50) На числовой прямой даны три отрезка: P = [10, 40], Q = [5, 15] и R=[35,50]. Выберите такой отрезок A, что формула

((x Î P) → (x Î Q)) \/ ((x Î A) → (x Î R))

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) [10, 20] 2) [15, 25] 3) [20, 30] 4)[120, 130]

51) На числовой прямой даны три отрезка: P = [0,20], Q = [5, 15] и R=[35,50]. Выберите такой отрезок A, что формула

((x Î P) → (x Î Q)) \/ ((x Î A) → (x Î R))

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) [-15,-5] 2) [2, 7] 3) [10,17] 4)[15, 20]

52) На числовой прямой даны три отрезка: P = [15,30], Q = [0, 10] и R=[25,35]. Выберите такой отрезок A, что формула

((x Î P) → (x Î Q)) \/ ((x Î A) → (x Î R))

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) [10,17] 2) [15, 25] 3) [20,30] 4)[35, 40]

53) На числовой прямой даны три отрезка: P = [20,50], Q = [15, 20] и R=[40,80]. Выберите такой отрезок A, что формула

((x Î P) → (x Î Q)) \/ ((x Î A) → (x Î R))

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) [10,25] 2) [20, 30] 3) [40,50] 4)[35, 45]

54) На числовой прямой даны три отрезка: P = [10,50], Q = [15, 20] и R=[30,80]. Выберите такой отрезок A, что формула

((x Î P) → (x Î Q)) \/ ((x Ï A) → (x Ï R))

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) [10,25] 2) [25, 50] 3) [40,60] 4)[50, 80]

55) На числовой прямой даны три отрезка: P = [0,40], Q = [20, 45] и R=[10,50]. Выберите такой отрезок A, что формула

((x Î P) → (x Î Q)) \/ ((x Ï A) → (x Ï R))

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) [5,20] 2) [10, 15] 3) [15,20] 4)[35,50]

56) На числовой прямой даны два отрезка: P = [5, 15] и Q = [10,20]. Выберите такой отрезок A, что формула

(x Î P) /\ (x Ï Q) /\ (x Î A)

тождественно ложна, то есть принимает значение 0 при любом значении переменной х.

1) [0, 7] 2) [8, 15] 3) [15, 20] 4)[7, 20]

57) На числовой прямой даны два отрезка: P = [12, 22] и Q = [7,17]. Выберите такой отрезок A, что формула

(x Ï P) /\ (x Î Q) /\ (x Î A)

тождественно ложна, то есть принимает значение 0 при любом значении переменной х.

1) [0, 5] 2) [7, 12] 3) [10, 20] 4)[5, 22]

58) На числовой прямой даны два отрезка: P = [10, 20] и Q = [5,15]. Выберите такой отрезок A, что формула

((x Î Q) → (x Î P)) /\ (x Î A)

тождественно ложна, то есть принимает значение 0 при любом значении переменной х.

1) [0, 6] 2) [5, 8] 3) [7, 15] 4)[12, 20]

59) На числовой прямой даны три отрезка: P = [15, 30], Q = [5,10] и R=[20,25]. Выберите такой отрезок A, что формула

((x Î P) → (x Î Q)) /\ ((x Ï A) → (x Î R))

тождественно ложна, то есть принимает значение 0 при любом значении переменной х.

1) [0, 20] 2) [0, 10] 3) [10, 15] 4)[25, 30]

60) На числовой прямой даны три отрезка: P = [15, 30], Q = [5,10] и R=[10,20]. Выберите такой отрезок A, что формула

((x Î P) → (x Î Q)) /\ (x Ï A) /\ (x Î R)

тождественно ложна, то есть принимает значение 0 при любом значении переменной х.

1) [0, 12] 2) [10, 17] 3) [15, 20] 4)[15, 30]

61) На числовой прямой даны три отрезка: P = [10,15], Q = [10,20] и R=[5,15]. Выберите такой интервал A, что формулы

(x Î A) → (x Î P) и (x Î Q) → (x Î R)

тождественно равны, то есть принимают равные значения при любом значении переменной х (за исключением, возможно, конечного числа точек).

1) [5, 12] 2) [10, 17] 3) [12, 20] 4)[15, 25]

62) На числовой прямой даны три отрезка: P = [5,10], Q = [15,20] и R=[25,30]. Выберите такой интервал A, что формулы

(x Î A) → (x Î P) и (x Î Q) → (x Ï R)

тождественно равны, то есть принимают равные значения при любом значении переменной х (за исключением, возможно, конечного числа точек).

1) [5, 10] 2) [15, 20] 3) [10, 20] 4)[15, 25]

63) На числовой прямой даны три отрезка: P = [10,25], Q = [15,30] и R=[25,35]. Выберите такой интервал A, что формулы

(x Ï A) → (x Ï P) и (x Î Q) → (x Î R)

тождественно равны, то есть принимают равные значения при любом значении переменной х (за исключением, возможно, конечного числа точек).

1) (10, 12) 2) (0, 10) 3) (5, 15) 4)(15, 25)

64) На числовой прямой даны три отрезка: P = [10,30], Q = [15,30] и R=[20,35]. Выберите такой интервал A, что формулы

(x Ï A) → (x Ï P) и (x Î Q) → (x Ï R)

тождественно равны, то есть принимают равные значения при любом значении переменной х (за исключением, возможно, конечного числа точек).

1) (10, 25) 2) (15, 20) 3) (15, 30) 4)(5, 20)

65) На числовой прямой даны три отрезка: P = [5,15], Q = [10,20] и R=[15,20]. Выберите такой интервал A, что формулы

(x Î A) → (x Î P) и (x Ï Q) → (x Ï R)

тождественно равны, то есть принимают равные значения при любом значении переменной х (за исключением, возможно, конечного числа точек).

1) [3, 10] 2) [7, 12] 3) [12, 17] 4)[22, 25]

66) На числовой прямой даны три отрезка: P = [5,25], Q = [5,15] и R=[10,20]. Выберите такой интервал A, что формулы

(x Ï A) → (x Ï P) и (x Ï Q) → (x Î R)

тождественно различны, то есть принимают разные значения при любом значении переменной х (за исключением, возможно, конечного числа точек).

1) (5, 12) 2) (10, 18) 3) (18, 25) 4)(20, 35)

67) На числовой прямой даны два отрезка: P = [3, 9] и Q = [4, 12]. Выберите такой отрезок A, что формула

((x Î А) → (x Î P)) \/ (x Î Q)

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) [0, 5] 2) [5, 10] 3) [10, 15] 4)[15, 20]

68) На числовой прямой даны два отрезка: P = [4, 16] и Q = [9, 18]. Выберите такой отрезок A, что формула

((x Î А) → (x Î P)) \/ (x Î Q)

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) [1, 11] 2) [3, 10] 3) [5, 15] 4)[15, 25]

69) На числовой прямой даны два отрезка: P = [3, 13] и Q = [7, 17]. Выберите такой отрезок A, что формула

((x Î А) → (x Î P)) \/ Ø(x Î Q)

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) [5, 20] 2) [10, 25] 3) [15, 30] 4)[20, 35]

70) На числовой прямой даны два отрезка: P = [5, 15] и Q = [11, 21]. Выберите такой отрезок A, что формула

((x Î А) → (x Î P)) \/ Ø(x Î Q)

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) [2, 22] 2) [3, 13] 3) [6, 16] 4) [17, 27]

71) На числовой прямой даны два отрезка: Р = [30, 45] и Q = [40, 55]. Выберите такой отрезок А, что обе приведённые ниже формулы истинны при любом значении переменной х:

(Ø (x Î А)) → Ø(x Î P)

(x Î Q) → (x Î A)

 

Если таких отрезков несколько, укажите тот, который имеет большую длину.

1) [25,50] 2) [25,65] 3) [35,50] 4) [35,85]

72) На числовой прямой даны два отрезка: P = [41, 61] и Q = [11, 91]. Выберите такой отрезок A, что формула

((x Î P) → (x Î А)) /\ ((x Î A) → (x Î Q))

тождественно истинна, то есть принимает значение 1 при любом значении

переменной х. Если таких отрезков несколько, укажите тот, который имеет

большую длину.

1) [7, 43] 2) [7, 73] 3) [37, 53] 4) [37, 63]

 

73) На числовой прямой даны два отрезка: P = [32, 52] и Q = [12, 72]. Выберите такой отрезок A, что формула

((x Î P) → (x Î А)) /\ ((x Î A) → (x Î Q))

тождественно истинна, то есть принимает значение 1 при любом значении

переменной х. Если таких отрезков несколько, укажите тот, который имеет

большую длину.

1) [7, 53] 2) [7, 33] 3) [27, 53] 4) [27, 33]

74) (https://ege.yandex.ru) На числовой прямой даны два отрезка: P = [10,30] и Q = [20, 40]. Выберите такой отрезок A, что формула

(x Î A) → ((x Î P) º (x Î Q))

тождественно истинна, то есть принимает значение 1 при любом значении переменной х. Если таких отрезков несколько, укажите тот, который имеет большую длину.

1) [10, 19] 2) [21, 29] 3) [31, 39] 4) [9, 41]

75) (https://ege-go.ru) На числовой прямой даны два отрезка: P = [54,84] и Q = [64, 94]. Выберите такой отрезок A, что формула

(x Î A) → ((x Î P) º (x Î Q))

тождественно истинна, то есть принимает значение 1 при любом значении переменной х. Если таких отрезков несколько, укажите тот, который имеет большую длину.

1) [25, 40] 2) [45, 61] 3) [65, 82] 4) [75, 83]

76) (https://ege-go.ru) На числовой прямой даны два отрезка: P = [34,64] и Q = [74, 94]. Выберите такой отрезок A, что формула

(x Î A) → ((x Î P) º (x Î Q))

тождественно истинна, то есть принимает значение 1 при любом значении переменной х. Если таких отрезков несколько, укажите тот, который имеет большую длину.

1) [5, 33] 2) [25, 42] 3) [45, 71] 4) [65, 90]

77) (https://ege-go.ru) На числовой прямой даны два отрезка: P = [34,84] и Q = [44, 94]. Выберите такой отрезок A, что формула

(x Î A) → ((x Î P) → (x Î Q))

тождественно истинна, то есть принимает значение 1 при любом значении переменной х. Если таких отрезков несколько, укажите тот, который имеет большую длину.

1) [45, 60] 2) [65, 81] 3) [85, 102] 4) [105, 123]

78) (https://ege-go.ru) На числовой прямой даны два отрезка: P = [6, 16] и Q = [30, 50]. Отрезок A таков, что формула

((x Î А) → (x Î Q)) \/ (x Î P)

тождественно истинна, то есть принимает значение 1 при любом значении переменной х. Какова наибольшая возможная длина отрезка A?

1) 10 2) 20 3) 21 4)30

79) (https://ege-go.ru) На числовой прямой даны два отрезка: P = [10, 40] и Q = [30, 50]. Отрезок A таков, что формула

((x Î А) → (x Î Q)) \/ (x Î P)

тождественно истинна, то есть принимает значение 1 при любом значении переменной х. Какова наибольшая возможная длина отрезка A?

1) 10 2) 20 3) 30 4)40

80) На числовой прямой даны два отрезка: P = [2, 42] и Q = [22, 62]. Выберите такой отрезок A, что формула

(x Ï A) → ((x Î P) → (x Ï Q))

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) [3, 14] 2) [23, 32] 3) [43, 54] 4) [15, 45]

81) На числовой прямой даны два отрезка: P = [2, 42] и Q = [22, 62]. Выберите такой отрезок A, что формула

((x Î P) → (x Ï Q)) → (x Ï A)

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) [3, 14] 2) [23, 32] 3) [43, 54] 4) [15, 45]

82) На числовой прямой даны два отрезка: P = [3,33] и Q = [22, 44]. Выберите такой отрезок A, что формула

(x Î Q) → ((x Î P) → (x Î A))

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) [2, 20] 2) [10, 25] 3) [20, 40] 4) [25, 30]

83) На числовой прямой даны два отрезка: P = [3,33] и Q = [22, 44]. Выберите такой отрезок A, что формула

(x Î P) → ((x Î Q) → (x Î A))

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) [31, 45] 2) [21, 35] 3) [11, 25] 4) [1, 15]

84) На числовой прямой даны два отрезка: P = [23,58] и Q = [10,39]. Выберите из предложенных вариантов такой отрезок A, что логическое выражение

((x Î P) Ù (x Î A)) → ((x Î Q) Ù (x Î A))

тождественно истинно, то есть принимает значение 1 при любом значении переменной х.

1) [5, 20] 2) [20, 40] 3) [40, 55] 4) [5, 55]

85) На числовой прямой даны два отрезка: P = [20,70] и Q = [5,32]. Выберите из предложенных вариантов такой отрезок A, что логическое выражение

((x Î P) Ù (x Î A)) → ((x Î Q) Ù (x Î A))

тождественно истинно, то есть принимает значение 1 при любом значении переменной х.

1) [15, 35] 2) [20, 40] 3) [40, 65] 4) [75, 88]

86) На числовой прямой даны два отрезка: P = [23,58] и Q = [1,39]. Выберите из предложенных вариантов такой отрезок A, что логическое выражение

((x Î P) Ù (x Î A)) → ((x Î Q) Ù (x Î A))

тождественно истинно, то есть принимает значение 1 при любом значении переменной х.

1) [5, 30] 2) [15, 40] 3) [25, 50] 4) [35, 60]

87) На числовой прямой даны два отрезка: P = [8,39] и Q = [23,58]. Выберите из предложенных вариантов такой отрезок A, что логическое выражение

((x Î P) Ù (x Î A)) → ((x Î Q) Ù (x Î A))

тождественно истинно, то есть принимает значение 1 при любом значении переменной х.

1) [5, 30] 2) [15, 40] 3) [20, 50] 4) [35, 60]

88) Элементами множества А являются натуральные числа. Известно, что выражение

(x Î {2, 4, 6, 8, 10, 12}) → (((x Î {3, 6, 9, 12, 15}) Ù (x Î A)) → (x Î {2, 4, 6, 8, 10, 12}))

истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наименьшее возможное значение суммы элементов множества A.

89) Элементами множества А являются натуральные числа. Известно, что выражение

(x Î {2, 4, 6, 8, 10, 12}) Ú ((x Î {3, 6, 9, 12, 15}) → (x Î A))

истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наименьшее возможное значение произведения элементов множества A.

90) Элементами множества А являются натуральные числа. Известно, что выражение

(x Î {1, 2, 3, 4, 5, 6}) Ú ((x Î {3, 6, 9, 12, 15}) → (x Î A))

истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наименьшее возможное значение суммы элементов множества A.

91) Элементами множества А являются натуральные числа. Известно, что выражение

((x Î {3, 5, 7, 11, 12, 15}) → (x Î {5, 6, 12, 15})) Ú (x Î A)

истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наименьшее возможное значение произведения элементов множества A.

92) Элементами множества А являются натуральные числа. Известно, что выражение

((x Î {1, 3, 5, 7, 9, 12}) → (x Î {3, 6, 9, 12})) Ú (x Î A)

истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наименьшее возможное значение суммы элементов множества A.

93) Элементами множества А являются натуральные числа. Известно, что выражение

(x Î {2, 4, 8, 12, 15}) → ((x Î {3, 6, 8, 15}) Ú (x Î A))

истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наименьшее возможное значение произведения элементов множества A.

94) Элементами множества А являются натуральные числа. Известно, что выражение

((x Î {3, 5, 7, 11, 12}) → (x Î {5, 6, 12, 15})) Ú (x Î A)

истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наименьшее возможное значение суммы элементов множества A.

95) Элементами множества А являются натуральные числа. Известно, что выражение

((x Î {1, 3, 5, 7, 9, 11}) → (x Î {3, 6, 9, 12})) Ú (x Î A)

истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наименьшее возможное значение суммы элементов множества A.

96) Элементами множества А являются натуральные числа. Известно, что выражение

(x Î {2, 4, 8, 12, 15}) → ((x Î {3, 6, 8, 15}) Ú (x Î A))

истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наименьшее возможное значение произведения элементов множества A.

97) Элементами множества А являются натуральные числа. Известно, что выражение

(x Î {1, 2, 4, 8, 16}) Ù (x Î {3, 4, 9, 16}) Ú (x Î A)

истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наименьшее возможное количество элементов множества A.

98) Элементами множества А являются натуральные числа. Известно, что выражение

(x Î {2, 4, 8, 12, 16}) Ù (x Î {3, 6, 7, 15}) Ú (x Î {3, 6, 7, 15}) Ú (x Î A)

истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наименьшее возможное количество элементов множества A.

99) Элементами множества А являются натуральные числа. Известно, что выражение

(x Î A) → ((x Î {1, 2, 3, 4, 5, 6}) Ù (x Î {3, 5, 15})) Ú (x Î {3, 5, 15})

истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наименьшее возможное количество элементов множества A.

100) Элементами множества А являются натуральные числа. Известно, что выражение

(x Î A) →(x Î {1, 3, 7}) Ú ((x Î {1, 2, 4, 5, 6}) Ù (x Î {1, 3, 7}))

истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наименьшее возможное количество элементов множества A.

101) Элементами множества А являются натуральные числа. Известно, что выражение

(x Î A) →((x Î {1, 2, 3, 4}) Ú (x Î {1, 2, 3, 4, 5, 6}))

истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наименьшее возможное количество элементов множества A.

102) Элементами множества А являются натуральные числа. Известно, что выражение

(x Î A) → ((x Î {1, 12}) Ù (x Î {12, 13, 14, 15, 16}))

истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наименьшее возможное количество элементов множества A.

103) Элементами множества А являются натуральные числа. Известно, что выражение

(x Î A) →((x Î {1, 2, 4, 8}) Ú (x Î {1, 2, 3, 4, 5, 6}))

истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наименьшее возможное количество элементов множества A.

104) Элементами множества А являются натуральные числа. Известно, что выражение

((x Î A) Ù (x Î {3, 6, 9, 12})) Ú (x Î {1, 2, 3, 4, 5, 6})

истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наименьшее возможное количество элементов множества A.

105) На числовой прямой даны два отрезка: P = [44; 49] и Q = [28; 53]. Укажите наибольшую возможную длину такого отрезка A, что формула

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

106) На числовой прямой даны два отрезка: P = [43; 49] и Q = [44; 53]. Укажите наибольшую возможную длину такого отрезка A, что формула

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

107) На числовой прямой даны два отрезка: P = [12; 26] и Q = [30; 53]. Укажите наибольшую возможную длину такого отрезка A, что формула

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

108) На числовой прямой даны два отрезка: P = [15; 39] и Q = [44; 57]. Укажите наибольшую возможную длину такого отрезка A, что формула

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

109) На числовой прямой даны два отрезка: P = [5; 30] и Q = [14; 23]. Укажите наибольшую возможную длину такого отрезка A, что формула

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

110) Элементами множеств А, P и Q являются натуральные числа, причём P = { 2, 4, 6, 8, 10, 12, 14, 16, 18, 20} и Q = { 5, 10, 15, 20, 25, 30, 35, 40, 45, 50}. Известно, что выражение

((x Î A) → (x Î P)) Ù ((x Î Q) → (x Î A))

истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наибольшее возможное количество элементов множества A.

111) Элементами множеств А, P и Q являются натуральные числа, причём P = { 2, 4, 6, 8, 10, 12, 14, 16, 18, 20} и Q = { 3, 6, 9, 12, 15, 18, 21, 24, 27, 30 }. Известно, что выражение

((x Î A) → (x Î P)) Ù ((x Î Q) → (x Î A))

истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наибольшее возможное количество элементов множества A.

112) На числовой прямой даны два отрезка: P = [25, 50] и Q = [32, 47]. Отрезок A таков, что формула

((x Î A) → (x Î P)) → ((x Î A) → (x Î Q))

тождественно истинна, то есть принимает значение 1 при любом значении переменной х. Какова наибольшая возможная длина отрезка A?

113) На числовой прямой даны два отрезка: P = [25, 37] и Q = [32, 47]. Отрезок A таков, что формула

((x Î A) Ù (x Î P)) → ((x Î P) Ù (x Î Q))