В прямоугольных декартовых координатах

Двойные и криволинейные интегралы

 

Двойной интеграл и его свойства

Пусть функция определена в некоторой замкнутой области плоскости . Разобьем область произвольным образом на частей с площадями . Внутри каждой элементарной области 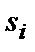выберем произвольную точку и найдем значение функции в этой точке. Составим сумму:

Эта сумма называется 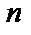-й интегральной суммой для функции по области .

Диаметром области 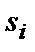назовем наибольшее из расстояний между точками границы этой области и обозначим .

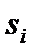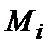Если существует конечный предел последовательности интегральных сумм при стремлении к нулю наибольшего из диаметров частичных областей , не зависящий ни от способа разбиения области , ни от выбора точек , то он называется двойным интегралом от функции по области и обозначается . Таким образом,

Если функция непрерывна в замкнутой области , то она интегрируема по этой области.

 

Свойства двойного интеграла

1.

2. .

3. Если область интегрирования разбить на две области и без общих внутренних точек, то

.

Вычисление двойного интеграла

в прямоугольных декартовых координатах

В прямоугольной системе координат элемент площади можно записать в виде произведения . Тогда

= .

Область называется правильной в направлении оси (или ), если любая прямая, проходящая параллельно этой оси, пересекает границу области не более, чем в двух точках.

Например, область на рис. 1 является неправильной в направлении оси и правильной в направлении оси (прямая пересекает границу области в четырех точках).

D

y

x

M

N

 

Рис. 1

 

Вычисление двойного интеграла сводится к вычислению повторного интеграла следующим образом.

1) Пусть область является правильной в направлении оси и ограничена линиями: , причем , (рис. 2).

a

b

A

B

x

y

y

Рис. 2

При выборе внешнего интегрирования по переменной x (из рис. 2 видно ) для определения внутренних пределов интегри­рования по переменной y по области интегрирования проводим прямую, параллельную оси снизу вверх. Прямая сначала пресекает кривую , которую назовем линией входа. При выходе из области интегрирования прямая пересечет кривую , которую назовем линией выхода. То есть значение переменной в области меняется в пределах .

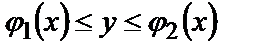Тогда = .

Правая часть формулы называется повторным интегралом.

Таким образом, вычисление двойного интеграла свелось к вычислению повторного (двух определенных интегралов) интеграла вида

.

При вычислении «внутреннего интеграла» (записанного в квадратных скобках) x считается постоянным.

2) Аналогичная формула вычисления двойного интеграла справедлива в случае, когда является правильной в направлении оси и ограничена линиями: 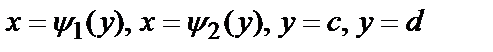, причем , (рис. 3).

x

y

C

D

c

d

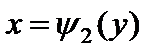
x

Рис. 3

Тогда = .

При вычислении «внутреннего интеграла» y считается постоянным.

Формулы перехода от двойного интеграла к повторному показывают, что в двойном интеграле можно изменять порядок интегрирования

.

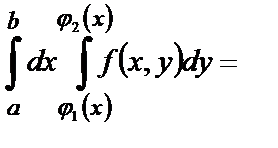
Если область интегрирования является неправильной, то ее можно представить как объединение правильных областей. Тогда двойной интеграл равен сумме двойных интегралов по этим областям.

Пример 1. В двойном интеграле расставить пре­делы интегрирования двумя способами, если область ограничена линиями , , .

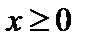Решение. Построим область (рис. 4). Найдем точки пересечения линий , , решая систему уравнений,

, , ,

, .

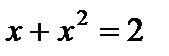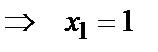Например, из первого уравнения системы находим: , . Таким образом парабола и прямая пересекаются в двух точках с координатам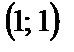и и , одна из которых принадлежит границе области (рис. 14).

A (2,0)

O (0,0)

y

x

B (1,1)

Рис. 4

Внешнее интегрирование по переменной .

Область интегрирования расположена между прямыми , , а переменная изменяется в данной области при каждом фик­сированном значении от точек параболы до точек прямой (рис. 11.4). Следовательно,

.

Внешнее интегрирование по переменной .

Так как верхний участок границы OBA области задан двумя ли­ниями OB и BA, то прямая разбивает область на области , и , . В результате получаем сумму двух повторных интегралов:

.

Пример 2. Вычислить двойной интеграл , если область ограничена линиями , , .

Решение. Построим область (рис. 5).

Найдем точки пересечения линий из системы уравнений , , ,

, .

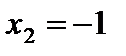Таким образом, 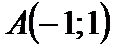– точка пересечения линий в рассматри-ваемой области.

Область интегрирования расположена между прямыми , , снизу ограничена прямой , сверху – параболой (рис. 5).

>

-1

x

y

A

Рис. 5

Следовательно,

.

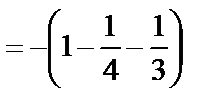
Если проводить внешнее интегрирование по переменной , то об­ласть необходимо разбивать на две области прямой и считать не один, а сумму двух повторных интегралов.