Тест – задание на внимательность.

Тема урока: Решение задач на тему «Пирамида»

Цели урока:

Обучающие: обобщить изученный материал. Вспомнить понятие правильной пирамиды. Рассмотреть задачи, связанные с пирамидой и с правильной пирамидой.
Развивающая: развивать познавательный интерес через творческую активность, исследовательскую деятельность на основе умения делать обобщения по данным, полученным в результате исследования.
Воспитательная: развивать эмоционально-положительное отношение к изучению геометрии, геометрическую зоркость, пространственное воображение.

Технология: проблемная.

Форма работы: групповая, индивидуальная.

Тип урока: обобщение изученного материала

Структура 1-го урока:

1. Организационный момент.

2. Актуализация знаний..

3. Решение задач.

4. Итог урока.

Оборудование: учебник геометрии 10-11-й класс, авторы Л.С.Атанасян, на столе модели геометрических тел.

Ход урока:

Организационный момент.

Актуализация знаний.

Как называются эти тела (модели демонстрирует учитель (тема “ многогранники” карточка ресурса № 34042)?

Что это за многогранник? (модель тетраэдра)

А кто помнит его определение? (поверхность, состоящая из четырех правильных треугольников или многогранник, состоящий их четырех треугольников)

Опишите эти фигуры (на столе модели различных пирамид)

Что объединяет эти тела? (в основании n-угольник, боковые грани – треугольники).

Как называются эти тела? (пирамиды)

Групп, 5 моделей (каждая группа сама выбирает себе модель). У каждого члена группы записи исследований в тетради.

Задание: п.п. 28,29- время работы 20 мин. (слайд 9)

Описать по алгоритму и определить сходство и различие между пирамидами в каждой группе:

1.Определение.
2.Основание.
3.Боковая грань.
4. Вершины.
5. Ребра.
6. Площадь боковой поверхности.
7. Площадь полной поверхности.

Далее идут презентации от каждой группы (каждая группа описывает свою модель пирамиды и показывает вычисления площади боковой поверхности и полной поверхности своей модели).

Затем устанавливаем сходство и различие между пирамидами в каждой группе, и даем определение пирамиды и правильной пирамиды.

Итак: мы рассмотрели определение пирамиды, элементы, построение пирамиды.

 

Применим эти знания при решении простейших задач.

Задача № 1

 

 

В правильной треугольной пирамиде SABC точка L − середина ребра AC, S − вершина. Известно, что BC=6, а SL=5. Найдите площадь боковой поверхности пирамиды.

 

В пра­виль­ной тре­уголь­ной пи­ра­ми­де SABC точка L — се­ре­ди­на ребра AC, S — вер­ши­на. Из­вест­но, что BC = 6, а SL = 5. Най­ди­те пло­щадь бо­ко­вой по­верх­но­сти пи­ра­ми­ды.

Ре­ше­ние.

От­ре­зок SL яв­ля­ет­ся ме­ди­а­ной пра­виль­но­го тре­уголь­ни­ка SAC, а зна­чит, и его вы­со­той. Бо­ко­вые грани пи­ра­ми­ды равны, по­это­му

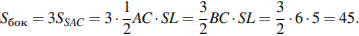
Ответ: 45.

 

 

Задача № 2

В пра­виль­ной че­ты­рех­уголь­ной пи­ра­ми­де точка – центр ос­но­ва­ния, – вер­ши­на, =12, =18. Най­ди­те бо­ко­вое ребро

Ре­ше­ние.

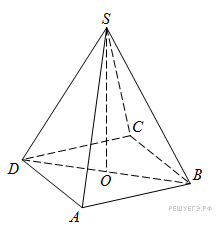
в пра­виль­ной пи­ра­ми­де вер­ши­на про­еци­ру­ет­ся в центр ос­но­ва­ния, сле­до­ва­тель­но 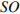яв­ля­ет­ся вы­со­той пи­ра­ми­ды. тогда по тео­ре­ме Пи­фа­го­ра

 

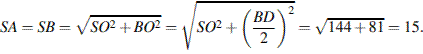
Ответ: 15.

 

 

Задача № 3

 

 

В пра­виль­ной тре­уголь­ной пи­ра­ми­де — се­ре­ди­на ребра , — вер­ши­на. Из­вест­но, что 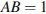, а 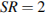. Най­ди­те пло­щадь бо­ко­вой по­верх­но­сти.

Ре­ше­ние.

 

Пло­щадь бо­ко­вой по­верх­но­сти пра­виль­ной тре­уголь­ной пи­ра­ми­ды равна по­ло­ви­не про­из­ве­де­ния пе­ри­мет­ра ос­но­ва­ния на апо­фе­му:

 

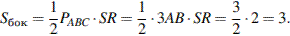
Ответ:3.

 

Задача № 4

 

В пра­виль­ной че­ты­рех­уголь­ной пи­ра­ми­де точка − центр ос­но­ва­ния, − вер­ши­на, 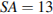, 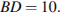Най­ди­те длину от­рез­ка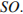

 

Ре­ше­ние.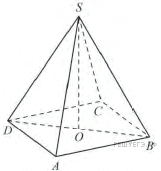

 

В пра­виль­ной пи­ра­ми­де вер­ши­на про­еци­ру­ет­ся в центр ос­но­ва­ния, сле­до­ва­тель­но, 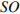яв­ля­ет­ся вы­со­той пи­ра­ми­ды. Тогда по тео­ре­ме Пи­фа­го­ра

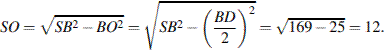
Ответ: 12.

 

Задача № 5

 

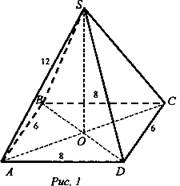
Дано: SABCD - пирамида; ABCD — прямоугольник; SO = 12 (см); АВ = 6 (см); ВС = 8 (см) (рис. 1).

Найти: SD.

Решение:

Пусть SABCD - данная пирамида, SO ⊥ ABCD. ΔABD - прямоугольный. По теореме Пифагора получим: 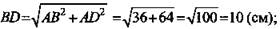ВО = OD = 5 (см); ΔSOD – прямоугольный треугольник.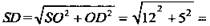

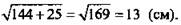
(Ответ: SD = 13 см.)

Задача № 6

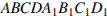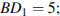
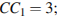
B 9 № 916. В пря­мо­уголь­ном па­рал­ле­ле­пи­пе­де из­вест­но, что 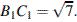Най­ди­те длину ребра .

 

 

 

Ре­ше­ние.

По тео­ре­ме Пи­фа­го­ра

 

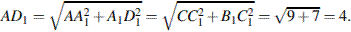
Тогда длина ребра равна

 

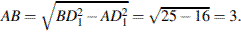
Ответ: 3.

Тест – задание на внимательность.

1.Сколько граней, боковых ребер у n-угольной пирамиды?

2. Какое наименьшее число граней может иметь пирамида?

3. Высота пирамиды равна 3см. Чему равно расстояние от вершины пирамиды до плоскости основания?

4. Боковые ребра треугольной пирамиды равны 7см, 12см, 5см. Одно из них перпендикулярно к плоскости основания. Чему равна высота пирамиды?

Рефлексия.

Подведем итоги нашей совместной работы.
Что нового узнали на сегодняшних уроках?
Какие знания пригодились?
Что было сложного?
Что понравилось на уроках?