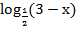Логарифмические уравнения.
Простейшее логарифмическое уравнение 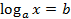 .
.
Логарифмическая функция возрастает (или убывает) на промежутке (0; 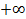 ) и принимает на этом промежутке все действительные значения.
) и принимает на этом промежутке все действительные значения.
По теореме о корне отсюда следует, что для любого b данное уравнение имеет, и причем только одно, решение. Из определения логарифма числа сразу следует, что 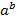 является таким решением, то есть х =
является таким решением, то есть х = 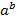 .
.
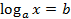
х = 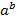 .
.
Пример1: Решить уравнение 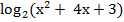 = 3.
= 3.
По определению логарифма: 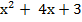 = 23
= 23
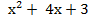 = 8
= 8
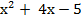 = 0
= 0
Решаем квадратное уравнение: D= 42 – 4· 1 · (–5) =36
х1 = 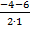 =
=  = – 5 и х2 =
= – 5 и х2 = 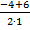 =
= 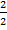 = 1.
= 1.
Следовательно, числа 1 и –5 являются решениями данного уравнения.
Ответ: –5; 1.
Пример2: Решить уравнение 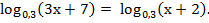
Это уравнение определено для тех значений х, при которых выполнены неравенства (под знаком логарифма может стоять только положительное число):
ОДЗ: 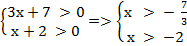
Значит, х ꞓ (−2; +∞).
Для этих х уравнение 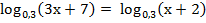 равносильно уравнению
равносильно уравнению
3х + 7 = х + 2
3х – х = 2 – 7
2х = –5
х = –2,5.
Число х = –2,5 не удовлетворяет ОДЗ (области допустимых значений х ꞓ (−2; +∞)). Следовательно, данное уравнение не имеет корней.
Ответ: Ø.
Пример3: Решить уравнение 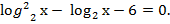
Сделаем замену переменной у = 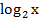 . Поэтому данное уравнение принимает вид:
. Поэтому данное уравнение принимает вид:
у2 – у – 6 = 0.
Решаем квадратное уравнение: D = (−1)2 – 4· 1 · (–6) = 25
у1 = 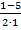 =
= 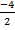 = – 2 и у2 =
= – 2 и у2 = 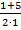 =
=  = 3.
= 3.
Получаем уравнения 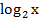 = –2
= –2 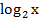 = 3
= 3
х = 2-2 х = 23
х = 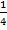 х = 8.
х = 8.
Ответ: 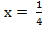 ; 8.
; 8.
Пример 4: Решить уравнение: 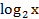 +
+ 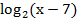 = 3.
= 3.
Это уравнение определено для тех значений х, при которых выполнены неравенства (под знаком логарифма могут стоять только положительные числа):
ОДЗ: 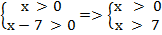
Значит, ОДЗ = (7; +∞).
Решаем непосредственно уравнение 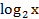 +
+ 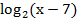 = 3.
= 3.
По свойству логарифмов loga(b·c) = logab + logac:
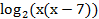 = 3.
= 3.
По определению логарифмов:
х(х – 7) = 23
Раскрываем скобки:
х2 − 7х = 8.
Переносим число 8 влево, поменяв знак, и решаем квадратное уравнение:
х2 − 7х − 8 = 0
D= (−7)2 – 4· 1 · (–8) = 81
х1 =  =
= 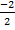 = – 1 и х2 =
= – 1 и х2 = 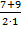 =
= 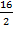 = 8.
= 8.
Число х = –1 не удовлетворяет ОДЗ (области допустимых значений х ꞓ (7; +∞)).
Следовательно, х = −1 – посторонний корень.
Число х = 8 удовлетворяет ОДЗ (области допустимых значений х ꞓ (7; +∞)).
Следовательно, х = 8 – корень уравнения.
Ответ: х = 8.
Логарифмические неравенства
1. Решение простейших логарифмических неравенств основано на известном свойстве функции
y = 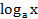 : эта функция возрастает при a > 1 и убывает при 0 < a < 1.
: эта функция возрастает при a > 1 и убывает при 0 < a < 1.
Пример 1: Решить неравенство 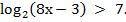
Представим число 7 в виде логарифма: 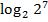 =
= 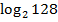 .
.
Поэтому данное неравенство можно переписать в виде 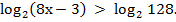
Логарифмическая функция с основанием 2 определена и возрастает на множестве действительных положительных чисел, так как 2 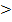 1.
1.
Убираем знаки логарифмов и знак неравенства не меняем 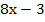
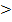 128.
128.
Выражение, стоящее под знаком логарифма должно быть больше 0, а у нас уже больше 128. Значит все х будут удовлетворять ОДЗ.
Решаем неравенство:
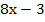
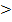 128
128
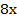
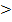 128 + 3
128 + 3
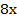
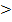 131
131
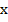
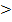 131: 8
131: 8
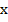
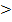 16,375
16,375
Ответ: х  (16,375; +∞).
(16,375; +∞).
Пример 2: Решить неравенство 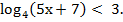
Представим число 3 в виде логарифма: 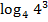 =
= 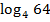 . Поэтому данное неравенство можно переписать в виде
. Поэтому данное неравенство можно переписать в виде 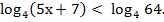
Логарифмическая функция с основанием 4 определена и возрастает на множестве действительных положительных чисел, так как 4 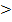 1. Убираем знаки логарифмов и знак неравенства не меняем 5х + 7
1. Убираем знаки логарифмов и знак неравенства не меняем 5х + 7 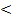 64.
64.
Так как выражение, стоящее под знаком логарифма должно быть больше 0, добавляем второе неравенство 5х + 7 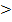 0.
0.
Получаем систему неравенств: 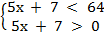
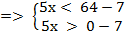
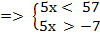
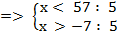
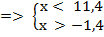
Ответ: х  (–
(– 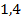 ; 11,4).
; 11,4).
Пример3: Решить неравенство 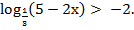
Представим число –2 в виде логарифма: 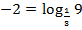 . Поэтому данное неравенство можно переписать в виде
. Поэтому данное неравенство можно переписать в виде 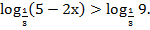
Логарифмическая функция с основанием  определена и убывает на множестве действительных положительных чисел, так как 0 ˂
определена и убывает на множестве действительных положительных чисел, так как 0 ˂ 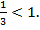 Следовательно, второму неравенству удовлетворяют такие числа х, (1. убираем знаки логарифмов, а знак неравенства меняется на противоположный, 2. выражение, стоящее под знаком логарифма должно быть больше 0), для которых выполнено условие:
Следовательно, второму неравенству удовлетворяют такие числа х, (1. убираем знаки логарифмов, а знак неравенства меняется на противоположный, 2. выражение, стоящее под знаком логарифма должно быть больше 0), для которых выполнено условие:
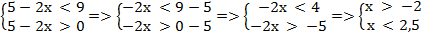
Ответ: х  (–
(– 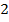 ; 2,5).
; 2,5).
Задание:
1. Решите уравнения:
1. 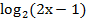 = 3
= 3
2. 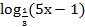 = −4
= −4
3. 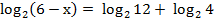
4. 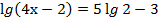
5. 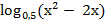 = −3
= −3
2. Решить неравенства:
1) 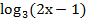 < 3
< 3
2) 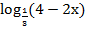 > −1
> −1
3) 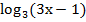 <
< 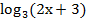
4) 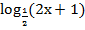 ≥
≥