Геометрические векторы
Геометрическим вектором называется направленный отрезок или, что то же самое, упорядоченная пара точек.
Направление на отрезке указывают стрелкой.

Обозначения: 
Расстояние между началом и концом вектора называется длиной вектора,обозначения: 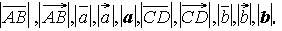
Векторы называются коллинеарными, если они расположены на одной прямой или на параллельных прямых.
Векторы называются компланарными, если они расположены в в одной плоскости или в праллельных плоскостях.
Два вектора называются равными, если они коллинеарны, одинаково направлены и равны по длине.
Вектор, у которого начало и коней совпадают, называют нулевым вектором: a = 0.
Противоположно направленные коллинеарные векторы равной длины называются противоположными.Обозначаются a и −a.
Вектор, длина которого равна 1, называется единичным.
Единичный вектор, направление которого совпадает с направлением вектора AB, называется ортом вектора AB и обозначается 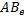 .
.
Углом между векторами называется угол образованный векторами, равными данным и имеющими общее начало.
Векторы, угол между которыми равен π/2, называются ортогональными.
Линейные операции с геометрическими векторами
Линейными операциями над векторам называются операции сложения векторов и умножения вектора на число.
Суммой векторов AB и BC называется вектор AC = AB + BC с началом в точке A и концом в точке C (правило треугольника).
Произведением вектора a и действительного числа α называется вектор α·a, длина которого равна |α|· |a|, направление совпадает с направлением вектора a при α > 0 и противоположно направлению вектора a при α < 0. Если α = 0, то α·a = 0.
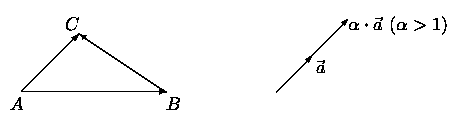
Свойства линейных операций с векторами
Для любых векторов a, b и c и любых чисел α, β саправедливо:
1. b + a = a + b;
2. a + (b + c) = (a + b) + c;
3. a + 0 = a (0 — нулевой вектор);
4. a + (−a) = 0 (− a — противоположный вектор);
5. 1·a = a;
6. α·(β·a) = (αβ)·a;
7. (α + β)·a = α·a + β·a;
8. α·(a + b) = α·a + α·b.
Условие коллинеарности векторов: два ненулевых вектора a и b коллинеарны тогда и только тогда, когда они пропорциональны, т.е. существует число α ≠ 0 такое, что a = α·b.
Нулевой вектор считается коллинеарным любому вектору.
Разложение вектора по базису
Любые два упорядоченные неколлинеарные вектора e1 и e2 образуют базис на плоскости.
Выражение a = α1·e1 + α2·e2 называется разложением вектора a по базису e1, e2.
Разложение вектора в базисе единственно.Числа α1, α2 называются координатами вектора в базисе e1, e2. Обозначаем: a = (α1, α2).

Любые три упорядоченные некомпланарные вектора e1, e2 и e3 образуют базис в пространстве.
Выражение a = α1·e1 + α2·e2 + α3·e3 называется разложением вектора a по базису e1, e2, e3
Разложение вектора в базисе единственно. Числа α1, α2, α3 называются координатами вектора в базисе e1, e2, e3. Обозначаем: a = (α1, α2, α3).

Линейные операции над векторам в координатной форме:
a = α1·e1 + α2·e2, b = β1·e1 + β2·e2,
c·a = (c·α1)·e1 + (c·α2)·e2,
a + b = (α1+β1)·e1 + (α2+β2)·e2;
a = α1·e1 + α2·e2+ α3·e3, b = β1·e1 + β2·e2+ β3·e3,
c·a = (c·α1)·e1 + (c·α2)·e2+ (c·α3)·e3,
a + b = (α1+β1)·e1 + (α2+β2)·e2+ (α3+β3)·e3.
Для того чтобы векторы были коллинеарны, необходимо и достаточно, чтобы их координаты были пропорциональны.
Если вектры, образующие базис, попарно ортогональны и имеют единичную длину, то базис называется ортонормированным.
Векторы ортонормированного базиса на плоскости обычно обозначают i и j.
Векторы ортонормированного базиса в пространстве обычно обозначают i, j и k.
Два вектора образуют упорядоченную пару векторов, если указано, какой из них первый, а какой — второй.
Три вектора образуют упорядоченную тройку векторов, если указано, какой из них является первым, а какой — вторым и какой — третьим.
Упорядоченная тройка векторов образует правую тройку, если, после приведения к общему началу, из конца третьего вектора кратчайший поворот от первого вектора ко второму виден против часовой стрелки.
В противном случае векторы образуют левую тройку.
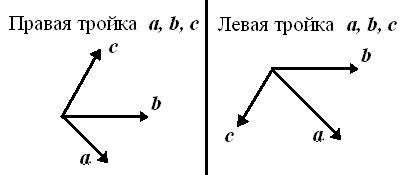
Векторы ортонормированного базиса i, j и k, направленные соответственно по осям абсцисс, ординат и аппликат, образуют правую тройку.