Скалярным произведением геометрических векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
Обозначается (a, b): (a, b) = |a|·|b|·cosφ.
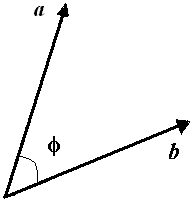
Если векторы a и b заданы своими координатами в ортонормированном базисе, то:
на плоскости — a = (α1, α2), b = (β1, β2), (a, b) = α1·β1 + α2·β2;
в пространстве — a = (α1, α2, α3), b = (β1, β2, β3), то (a, b) = α1·β1 + α2·β2 + α3·β3.
Свойства скалярного произведения геометрических векторов
Для любых векторов a, b и c и любых чисел α, β справедливо:
• (a, b) = (b, a);
• (a + b, c) = (a,c) + (b,c);
• (α·a, b) = α·(a, b);
• (a,a) = |a|2 ≥ 0; (a,a) = 0 тогда и только тогда, когда a = 0;
• скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда векторы ортогональны;
• если вектор и задан своими координатами в ортонормированном базисе, то:
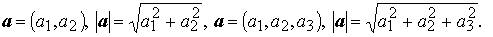
Векторное произведение геометрических векторов
Векторным произведением геометрических векторов a и b называется вектор c = [a, b], который определяются следующим образом:
1) |c| = |[a, b]|;= |a|·|b|·sinφ;
2) вектор c ортогонален вектору a и вектору b;
3) векторы a, b и c образуют правую тройку векторов.
Легко видеть, что длина векторного произведения равна площади параллелограмма, построенного на векторах-сомножителях как на сторонах.

Если векторы a и b заданы своими координатами в ортонормированном базисе e1, e2, e3:
a = (α1, α2, α3), b = (β1, β2, β3), то координаты вектороного произведения вычисляются по формуле:[a, b] = (α2·β3 − α3·β2, α3·β1 − α1·β3,α1·β2 − α2·β1). То есть, если a = α1·e1 + α2·e2 + α3·e3 и b = β1·e1 + β2·e2 +β3·e3, то[a, b] = (α2·β3 − α3·β2)·e1 + (α3·β1 − α1·β3)·e2 + (α1·β2 − α2·β1)·e3.
Свойства векторного произведения геометрических векторов
Для любых векторов a, b и c и любых чисел α, β саправедливо:
• [a, b] = −[b, a];
• [a + b, c] = [ a,c] + [b,c];
• [α·a, b] = α·[a, b];
• [a, b] = 0 тогда и только тогда, когда векторы a и b коллинеарны, (векторное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда векторы коллинеарны);
•площадь параллелограмма, построенного на векторах a и b как на сторонах, равна длине векторного произведения векторов a и b.
Смешанное произведение геометрических векторов
Число ([a, b], c) называется смешанным произведением векторов a, b и c, т.е. число, равное скалярному произведению векторного произведения [a, b] векторов a и b на вектор c.
Обозначается (a, b,c): (a, b,c) = ([a, b], c).
Если векторы a, b и c заданы своими координатами в ортонормированном базисе e1, e2, e3: a = (α1, α2, α3), b = (β1, β2, β3), c = (γ1,γ2, γ3), то
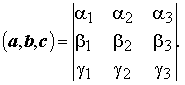
Смешанное произведение трёх некомпланарных векторов по абсолютной величине равно объёму параллелепипеда, построенного на сомножителях как на рёбрах.
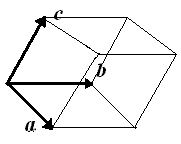
Смешанное произведение положительно, если сомножители образуют правую тройку и отрицательно — если левую.Смешанное произведение трёх векторов равно нулю тогда и только тогда, когда векторы компланарны.
Свойства смешанного произведения геометрических векторов
Для любых векторов a, b, c и d и любых чисел α, β саправедливо:
• (a, b, c) = (c, a, b) = (b, c, a) = −(b, a, c) = −(c, b, a) = −(a, c, b);
• (a + b, c, d) = (a, c, d) + (b, c, d);
• (α·a, b, c) = α·(a, b, c);
• (a, b, c) = 0, a ≠ 0, b≠ 0, c≠ 0, тогда и только тогда, когда векторы a, b и c компланарны (смешанное произведение трёх ненулевых векторов равно нулю тогда и только тогда, когда векторы компланарны)
• смешанное произведение положительно, если его сомножители образуют правую тройку и отрицательно, если они образуют левую тройку.