Тема 5: Средние показатели.
Сущность и значение средних показателей
Средняя величина (the mean) представляет собой обобщенную количественную характеристику признака статистической совокупности в конкретных условиях места и времени.
Показатель в форме средней величины отражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из варьирующих признаков. Сущность средней величины заключается в том, что в ней взаимопогашаются отклонения индивидуальных значений признака единиц совокупности, обусловленные действием случайных факторов, и, учитываются изменения, вызванные действием основных.
На практике определить среднюю во многих случаях можно, используя ее логическую формулу:
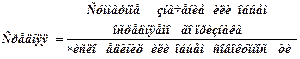
В зависимости от того, в каком виде представлены исходные данные для расчета средней, зависит, каким именно образом будет реализовано ее исходное соотношение.
Различают следующие виды средней, каждая из которых может быть простой и взвешенной:
· Средняя арифметическая;
· Средняя гармоническая;
· Средняя геометрическая;
· Средняя квадратическая, кубическая и т.д.
· Структурные средние: мода и медиана.
Средняя арифметическая и ее свойства.
Средняя арифметическая простая (the simple arithmetic mean). Эта форма средней используется в тех случаях, когда расчет осуществляется по не сгруппированным данным.
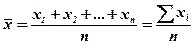
Средняя арифметическая взвешенная (the weighted arithmetic mean). При расчете средних величин отдельные значения признака могут повторяться, встречаться по нескольку раз. В данном случае расчет проводится по
сгруппированным данным или вариационным рядам, которые могут быть дискретными или интервальными.

Средняя арифметическая величина имеет следующие свойства, использование которых упрощает ее расчет.
1. Произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие им частоты.
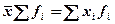
2. Сумма отклонений индивидуального значения признака от средней арифметической равна нулю:
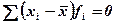
3. Если все осредняемые варианты уменьшить или увеличить на постоянное число А, то средняя арифметическая соответственно уменьшится или увеличится на туже величину.
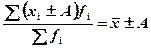
4. Если все варианты значений признака уменьшить или увеличить в А раз, то средняя соответственно уменьшится или увеличится в А раз:

5. Если все частоты уменьшить или увеличить в А раз, то средняя останется неизменной:

6. Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем сумма квадратов их отклонений от любой другой произвольной величины С:
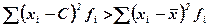
Другие виды средних величин.
Средняя гармоническая – это величина, обратная средней арифметической из обратных значений признака. Различают среднюю гармоническую простую и взвешенную.
Средняя гармоническая простая (the simple harmonic mean).

Средняя гармоническая взвешенная (the weighted harmonic mean) применяется тогда, когда статистическая информация не содержит частот по отдельным вариантам совокупности, а представлена как их произведение.

Средняя арифметическая и средняя гармоническая величины могут применятся в одних и тех же ситуациях, но по разным данным. Если в логической формуле неизвестен числитель, то в расчетах применяется средняя арифметическая величина. Если в логической формуле неизвестен знаменатель, то в расчетах используется средняя гармоническая величина.
Средняя квадратическая величина (the quadratic mean) применяется тогда, когда вместо индивидуальных значений признака представлены квадраты исходных величин.
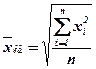
Средняя геометрическая (the geometric mean) применяется в случаях определения средней по значениям, имеющим большой разброс, либо в случаях определения средней величины по относительным показателям.
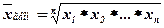
Средняя степенная. В математической статистике различные средние выводятся из формул степенной средней:
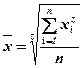
При z = 1 – средняя арифметическая;
z = –1 – средняя гармоническая;
z = 2 – средняя квадратическая.
Чем выше z, тем больше значения средней величины.