Задача 2.
Условия задачи и исходные данные: имеется установка «А», состоящая из четырех последовательно соединенных узлов. Схема расчета надежности установки изображена на рисунке.
Все элементы установки равнонадежны и для них справедлив экспоненциальный закон распределения наработки до отказа. Интенсивность отказов элементов равна 11 
(1/ч).
Требуется:
1. Вычислить и построить график изменения функции надежности узлов «а», «б», «в» и «г» установки «А» в течение 10000 ч с интервалом 2000 ч.
2. По результатам расчета вероятности безотказной работы узлов «а», «б» и «в» сделать вывод об эффективности различных видов резервирования.
3. Вычислить и построить график изменения функции надежности установки «А» в течение 10000 часов с интервалом 2000 ч.
4. Определить вероятность безотказной работы для системы из двух параллельно включенных установок «А» и «Б» по истечению года эксплуатации, если вероятность безотказной работы установки «Б» за год эксплуатации равна 0,92.
5. Определить годовую потребность запасных элементов для 3 установок «С » при заданной вероятности обеспечения запасными частями
Р z = 0,9.
Схема расчета надежности:
1. Провожу вычисления и строю график изменения надежности всех узлов в течение 10000 ч с интервалом 2000 ч:
В узле «а» применено общее резервирование с постоянным включением резерва и целой кратностью.
Вероятность безотказной работы в этом случае вычисляется по формуле:
Р а(t)=1-[1-ехр (-li t)]m+1,
где m – число резервных цепей (кратность резервирования);
n – число элементов основной и резервной цепи.
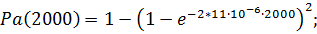
| Ра (2000) | = | 0,998 |
| Ра (4000) | = | 0,993 |
| Ра (6000) | = | 0,985 |
| Ра (8000) | = | 0,974 |
| Ра (10000) | = | 0,961 |
В узле «б» применено раздельное резервирование с постоянно включенным резервом и с целой кратностью. Вероятность безотказной работы в этом случае вычисляется по формуле
Р б(t)={1-[1-ехр (-lэ t)]m+1}n,
где n- число последовательно соединенных групп элементов.
;
| Рб (2000) | = | 0,999 |
| Рб (4000) | = | 0,996 |
| Рб (6000) | = | 0,992 |
| Рб (8000) | = | 0,986 |
| Рб (10000) | = | 0,978 |
В узле «в» применено общее резервирование замещением с целой кратностью и ненагруженном состоянии резерва. Вероятность безотказной работы в этом случае вычисляется по формуле:
Рв(t)=ехр (-li t) 
,
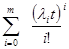где m – число резервных цепей (кратность резервирования);
n - число элементов основной цепи.
| Рв (2000) | = | 0,999 |
| Рв (4000) | = | 0,996 |
| Рв (6000) | = | 0,992 |
| Рв (8000) | = | 0,986 |
| Рв (10000) | = | 0,979 |
В узле «г» применено общее резервирование с дробной кратностью и постоянно включенным резервом. Число элементов, необходимых для нормальной работы в этом узле равно k= 2. Вероятность безотказной работы в этом случае вычисляется по формуле:
Р г(t) = 
,
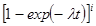где n – число элементов, l - интенсивность отказа одной цепи.
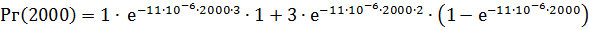
| Рг (2000) | = | 0,999 |
| Рг (4000) | = | 0,995 |
| Рг (6000) | = | 0,988 |
| Рг (8000) | = | 0,980 |
| Рг (10000) | = | 0,970 |
График изменения надежности всех узлов:
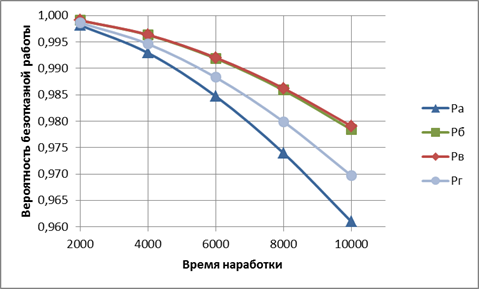
2. По результатам расчета вероятности безотказной работы узлов «а», «б» и «в» можно сделать вывод об эффективности различных видов резервирования:
При раздельном резервировании с постоянно включенным резервом и с целой кратностью, и при общем резервировании замещением с целой кратностью и ненагруженным состоянием резерва достигаются лучшие показатели надежности. Общее резервирование с дробной кратностью и постоянно включенным резервом дает относительно низкий показатель безотказной работы, а применение общего резервирования с постоянным включением резерва и целой кратностью приводит к наименьшим результатам.
3. Вычисляю и строю график изменения функции надежности установки «А» в течение 10000 часов с интервалом 2000 ч:
Вероятность безотказной работы установки «А» равна произведению вероятностей безотказной работы всех узлов:
РА (t) = Ра(t)·Рб(t)·Рв(t)·Рг(t)
| РА (2000) | = | 0,998 | * | 0,999 | * | 0,999 | * | 0,999 | = | 0,995 |
| РА (4000) | = | 0,993 | * | 0,996 | * | 0,996 | * | 0,995 | = | 0,980 |
| РА (6000) | = | 0,985 | * | 0,992 | * | 0,992 | * | 0,988 | = | 0,958 |
| РА (8000) | = | 0,974 | * | 0,986 | * | 0,986 | * | 0,980 | = | 0,928 |
| РА (10000) | = | 0,961 | * | 0,978 | * | 0,979 | * | 0,970 | = | 0,893 |
График изменения функции надежности установки «А»:
4. Определяю вероятность безотказной работы для системы из двух параллельно включенных установок «А» и «Б» по истечению года эксплуатации:
Часов в году принимаю значение 8760;
РА (8760) = 0,915
Вероятность безотказной работы для системы из двух параллельно включенных установок «А» и «Б» вычисляется по основной формуле для общего резервирования с постоянно включенным резервом и с целой кратностью для неравнонадежных установок:
Р АБ = 1-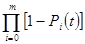 
=1-(1- Р А)(1- Р Б)
| PАБ= | ( | - | 0,915 | ) | (1 | - | 0,92 | ) | = | 0,99321 |
5. Определяю годовую потребность запасных элементов для 6 установок «С » при заданной вероятности обеспечения запасными частями Р z = 0,99.
Потребность в запасных частях определяется средним расходом элементов за определенный промежуток времени и заданной вероятностью Р z обеспечения запасными элементами, т.е. с какой вероятностью не будет простоев вследствие отсутствия запасных элементов для замены вышедших из строя.
При экспоненциальном распределении наработки до отказа среднее число отказавших элементов Z ср за период t определяю по формуле:
Z ср= N lэ t,
где N – число элементов, находящихся в эксплуатации;
lэ - интенсивность отказов одного элемента, 1/ч;
t – период работы, ч.
В соответствии с условиями задачи количество элементов всех установок, находящихся в эксплуатации в течение года, равно:
N= с · С,
где с - количество элементов одной установки, принимаю равным 20 шт.;
С - общее количество установок, находящихся в эксплуатации.
Z ср= с · С lэ t
| Z ср | = | * | * | * | -6 | = | 5,7816 | (шт). |
При Р z=0,9 число запасных элементов Z вычисляю по приближенной формуле:
Z =35+1,47zср при 20< z ср£60..70;
| Z | = | + | 1,47 | * | = | 14,82 | (шт). | |||
Ответ: При Р z=0,9 число запасных элементов Z=15