Лабораторная работа № 130
ОПРЕДЕЛЕНИЕ СКОРОСТИ ПУЛИ ПРИ ПОМОЩИ
БАЛЛИСТИЧЕСКОГО МАЯТНИКА
Аудитория Г-225
Лабораторная работа № 130
ОПРЕДЕЛЕНИЕ СКОРОСТИ ПУЛИ ПРИ ПОМОЩИ
БАЛЛИСТИЧЕСКОГО МАЯТНИКА
Цель работы. Определить скорость пули и потери механической энергии при неупругом взаимодействии «пули» и «ловушки», используя закон сохранения момента импульса, закон сохранения и превращения энергии.
Приборы и принадлежности: 1. Установка лабораторная.
2. Набор пуль.
Теоретическое введение.
В данной работе для определения скорости полета пули используется баллистический маятник. Баллистический маятник (Рис. 1) представляет собой физический маятник, состоящий из «ловушки» массой  , закрепленной на нижнем конце стержня массой
, закрепленной на нижнем конце стержня массой 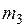 . Верхний конец стержня насажен на вал, закрепленный в подшипнике, так что вся система может свободно вращаться вокруг горизонтальной оси Z, проходящей через центр вала. После выстрела из пружинного пистолета пуля массой
. Верхний конец стержня насажен на вал, закрепленный в подшипнике, так что вся система может свободно вращаться вокруг горизонтальной оси Z, проходящей через центр вала. После выстрела из пружинного пистолета пуля массой 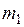 попадает в неподвижную ловушку и остается в ней. В результате абсолютно неупругого удара пули об ловушку маятник отклоняется от положения равновесия. Законы сохранения момента импульса и энергии позволяют найти скорость пули
попадает в неподвижную ловушку и остается в ней. В результате абсолютно неупругого удара пули об ловушку маятник отклоняется от положения равновесия. Законы сохранения момента импульса и энергии позволяют найти скорость пули 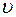 по величине угла отклонения
по величине угла отклонения  маятника от положения равновесия. На рис. 1 изображена система "пуля - маятник" в трех важных состояниях:
маятника от положения равновесия. На рис. 1 изображена система "пуля - маятник" в трех важных состояниях:
Состояние 1 - пуля вылетела из пистолета, но еще не долетела до ловушки. Ловушка неподвижна.
Состояние 2 - пуля попала в ловушку, которая вместе с пулей начала отклоняться от положения равновесия.
Состояние 3 - маятник отклонился на максимальный угол 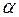 , и ловушка с пулей сместилась вдоль измерительной шкалы на расстояние S, которое измеряем в работе. При этом центр инерции ловушки с пулей поднимается на высоту Н относительно положения равновесия.
, и ловушка с пулей сместилась вдоль измерительной шкалы на расстояние S, которое измеряем в работе. При этом центр инерции ловушки с пулей поднимается на высоту Н относительно положения равновесия.
|
|
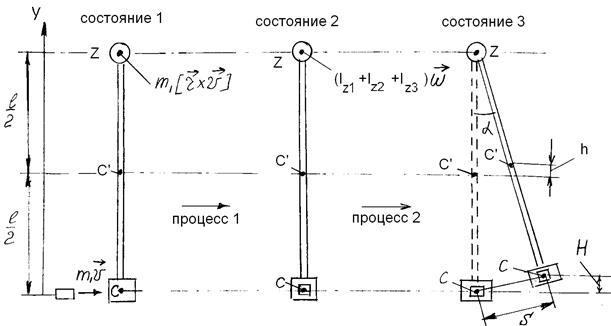
Рис. 1
Условно движение системы тел маятника можно представить двумя процессами.
В процессе 1 движущаяся пуля взаимодействует с ловушкой, и система переходит из состояния 1 в состояние 2. В этом процессе механическая энергия не сохраняется из-за ее частичного преобразования во внутреннюю энергию. При этом, однако, сохраняется момент импульса системы относительно оси вращения Z:
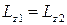 , (1)
, (1)
где LZ1 – проекция момент импульса системы на ось Z до взаимодействия:
 , (2)
, (2)
LZ2 - проекция момент импульса системы на ось Z после взаимодействия:

 (3)
(3)
В соотношении (3)  -полный момент инерции системы относительно оси Z,
-полный момент инерции системы относительно оси Z,  ,
, 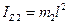 ,
, 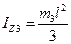 - соответственно моменты инерции пули, ловушки и стержня маятника относительно оси Z.
- соответственно моменты инерции пули, ловушки и стержня маятника относительно оси Z.
После абсолютно неупругого захвата пули в ловушку маятник начинает вращаться вокруг оси Z с угловой скоростью 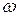 . Из выражений (2) и (3) следует, что начальная угловая скорость системы определяется соотношением
. Из выражений (2) и (3) следует, что начальная угловая скорость системы определяется соотношением
 (4)
(4)
Полная механическая энергия системы (равная энергии пружины или кинетической энергии пули) в процессе 1 не сохраняется, так как при движении пули в ловушке происходят многократные неупругие соударения пули со стенкой. В результате большая часть механической энергии системы 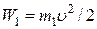 теряется на совершение работы неконсервативных сил, возникающих при деформациях пули и стенок ловушки. Величина потери энергии равна работе неконсервативных сил и равна разности первоначальной энергии системы и начальной энергии вращения маятника
теряется на совершение работы неконсервативных сил, возникающих при деформациях пули и стенок ловушки. Величина потери энергии равна работе неконсервативных сил и равна разности первоначальной энергии системы и начальной энергии вращения маятника
|
|
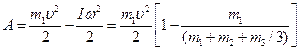 (5)
(5)
В процессе 2 (переход из второго состояния в третье) работу совершает лишь консервативная сила тяжести, поэтому к процессу 2 можно применить закон сохранения полной механической энергии:
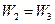 , (6)
, (6)
где
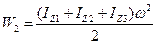 (7)
(7)
- кинетическая энергия вращательного движения системы в состоянии 2,
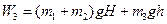 (8)
(8)
- потенциальная энергия системы в состоянии 3.
Из Рис. 1 следует, что изменение высоты центра масс С ловушки с пулей при переходе из состояния 2 в состояние 3 равно:
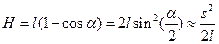 . (9)
. (9)
При этом изменение высоты центра масс стержня  в 2 раза меньше:
в 2 раза меньше:
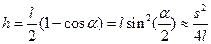 . (10)
. (10)
Здесь 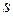 - перемещение центра ловушки из равновесного положения в его положение при максимальном отклонении, определяемое по шкале линейки 7.
- перемещение центра ловушки из равновесного положения в его положение при максимальном отклонении, определяемое по шкале линейки 7.
Из соотношений (6)-(10) найдем скорость пули
 (11)
(11)
Описание схемы установки.
Схема лабораторной установки представлена на Рис.2. На платформе 10 размещены пружинный пистолет 1, стойка 5 на которой закреплён вал с подшипником 4. На вал подшипника насажен верхний конец стержня 3 маятника, на нижнем конце которого закреплена ловушка 2.

|
| Рис. 2 |
Стержень ствола пистолета 1 находится на одном уровне с входным отверстием ловушки 2. Расстояние s, пройденное ловушкой, измеряется с помощью металлической линейки 7, которая фиксирует подвесную пластинку 6 ловушки 2 с помощью зубчатой поверхности линейки. Для сжатия пружины 8 необходимо пулю - полый металлический цилиндр надеть на стержень ствола пистолета, сжать пружину пулей, закрепив ее специальным фиксатором 9. Выстрел производится нажатием на фиксатор 9 вниз, в результате чего пуля влетит в ловушку. Маятник с пулей отклонится на угол 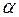 и останется в этом положении за счёт подвесной планки 6, зафиксированной зубцами линейки 7.
и останется в этом положении за счёт подвесной планки 6, зафиксированной зубцами линейки 7.
|
|
Выполнение работы.
Из таблицы (на платформе 10) занести в протокол расстояние от оси вращения до центра инерции ловушки l, массы пуль 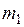 и
и  , а также массы ловушки
, а также массы ловушки  и стержня маятника
и стержня маятника 
1. Привести установку в исходное положение, для чего: установить стержень маятника так, чтобы он висел параллельно стойки 5; определить соответствующее положение  планки 6 по шкале линейки 7. Ловушку отцентрировать так, чтобы ось стержня ствола проходила через центр отверстия ловушки (т.е. так, чтобы пуля после выстрела попала в ловушку). Пули должны находиться на платформе 10. Значение
планки 6 по шкале линейки 7. Ловушку отцентрировать так, чтобы ось стержня ствола проходила через центр отверстия ловушки (т.е. так, чтобы пуля после выстрела попала в ловушку). Пули должны находиться на платформе 10. Значение 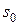 занести в табл. 1.
занести в табл. 1.
2. Надеть пулю массой 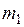 на стержень ствола пистолета и сжать пружину пулей влево и закрепить её фиксатором 9 за третий виток пружины от ее конца. При последующих повторных измерениях производить фиксацию пружины за тот же виток.
на стержень ствола пистолета и сжать пружину пулей влево и закрепить её фиксатором 9 за третий виток пружины от ее конца. При последующих повторных измерениях производить фиксацию пружины за тот же виток.
3. Нажать на фиксатор пружины вниз и произвести выстрел из пистолета по маятнику. Пуля влетит в ловушку и отклонит маятник от исходного положения. Планка 6 зафиксирует крайнее положение 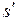 отклоненного маятника по шкале линейки 7. Найти разницу между начальным и конечным положением планки 6 по шкале линейки 7:
отклоненного маятника по шкале линейки 7. Найти разницу между начальным и конечным положением планки 6 по шкале линейки 7: 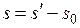 . Результаты занести в таблицу 1.
. Результаты занести в таблицу 1.
4. Вынуть пулю из ловушки, отклонив маятник вправо. Возвратить систему в исходное положение.
5. Опыт повторить два раза по пп. 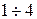 . Результаты занести в таблицу 1.
. Результаты занести в таблицу 1.
6. Заменить пулю массой 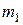 на пулю массой
на пулю массой 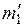 и провести три раза выполнение пунктов
и провести три раза выполнение пунктов 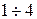 . Результаты измерений занести в табл. 1.
. Результаты измерений занести в табл. 1.
4. Обработка результатов наблюдений.
1. Для каждого значения перемещения, найденного в двух сериях опытов с разными значениями массы пули 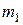 и
и 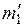 , рассчитать по формуле (11) значения скорости пули до удара и по формуле (5) работы А неконсервативных сил при ударе пули и ловушки. Результаты занести в таблицу 1.
, рассчитать по формуле (11) значения скорости пули до удара и по формуле (5) работы А неконсервативных сил при ударе пули и ловушки. Результаты занести в таблицу 1.
2. Для каждой массы пули рассчитать средние значения скорости пули 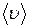 и работы
и работы 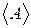 . Результаты занести в таблицу 1.
. Результаты занести в таблицу 1.
3. Вычислить относительные погрешности измерений 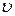 и A как для косвенных измерений, приравняв их приближенно относительной погрешности определения длины перемещения
и A как для косвенных измерений, приравняв их приближенно относительной погрешности определения длины перемещения 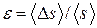 . (для нахождения случайной ошибки
. (для нахождения случайной ошибки  определить стандартной процедурой среднеквадратичную ошибку и умножить ее на соответствующий числу измерений коэффициент Стьюдента). Результаты занести в таблицу 1.
определить стандартной процедурой среднеквадратичную ошибку и умножить ее на соответствующий числу измерений коэффициент Стьюдента). Результаты занести в таблицу 1.
4. Записать окончательные результаты для двух значений массы пули в виде:
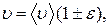

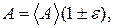

5. Сравнить результаты определения скорости и работы для двух значений массы пули и проанализировать их на основе формул (5), (11).
 Данные измерений и вычислений занести в табл. 1
Данные измерений и вычислений занести в табл. 1
Таблица 1
| № п/п |  , кг , кг
|  , м , м
| 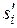 ,м ,м
| 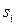 м м
| 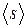 м м
|  , м , м
|  , м , м
| 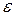
| 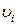 , м/c , м/c
| 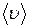 , м/c , м/c
|  ,
Дж ,
Дж
| 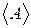 ,
Дж ,
Дж
|
 = =
| ||||||||||||
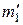 = =
| ||||||||||||
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Вывести расчетные формулы для 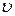 и А.
и А.
2. Как определить относительную погрешность измерений 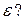
3. Почему при расчете относительной погрешности учитывалась только ошибка измерения длины перемещения?
4. Поясните преобразование одного вида энергии в другой после выстрела.
5. Какие силы называются неконсервативным и что они вызывают?
6. Почему при захвате пули в ловушку не сохраняется механическая энергия системы, но сохраняется ее момент импульса?
7. При каком ударе (упругом или неупругом) маятник отклонится на больший угол и почему?
8. Почему при проведении повторных наблюдений натяжение пружины устанавливается всегда одинаковым?