Билет № 9
1) Разность квадратов. Сумма и разность кубов. Разложение многочлена на множители с помощью этих формул.
I. Произведение суммы и разности двух выражений
 (a+b)(a-b)=a2-ab+ab – b2=a2-b2
(a+b)(a-b)=a2-ab+ab – b2=a2-b2
Произведение суммы и разности двух выражений равно разности квадратов этих выражений.
Примеры:
1. (2x-3)(2x+3)=4x2-9
2. (2y3-5y)(2y3+5y)=4y6 - 25y2
3. (12x2 – 17y3)(17y3+12x2)=144x4 – 289y6
4. (5a7+2a9)(2a9 – 5a7)=4a18-25a14
Разложение многочлена на множители с помощью формул сокращённого умножения
 | |||
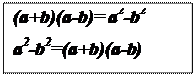 | |||
Примеры:
1. 64x2 - 9=(8x)2 - 32=(8x-3)(8x+3)
2. x6-4a4=(x3)2 – (2a2)2=(x3 – 2a2)(x3+2a2)
3. 225m4 - 169n6= (15m2)2 – (13n3)2=(15m2 – 13n3)(15m2+13n2)
II. Сумма кубов двух выражений

 (a+b)(a2–ab+b2)= a3- a2b+ ab2+a2b-ab2+b3=a3+b3
(a+b)(a2–ab+b2)= a3- a2b+ ab2+a2b-ab2+b3=a3+b3
|

 |
Примеры:
1. 27y3+8x3=(3y)3+(2x)3=(3y+2x)(9y2 -6xy+4x2)
2. 125m6+64n12=(5m2)3+(4n4)3=(5m2+4n4)(25m4-20m2n4+16n8)
3. (2x+y)(4x2-2xy+y2)=8x3+y3
4. (3m+2n)(9m2-6mn+4n2)=27m3+8n3
III. Разность кубов двух выражений

 (a-b)(a2 +ab+b2)= a3+a2b + ab2-a2b- ab2 - b3=a3 - b3
(a-b)(a2 +ab+b2)= a3+a2b + ab2-a2b- ab2 - b3=a3 - b3
|
Пример: 27y12 - 125x15=(3y4)3 – (5x5)3=(3y4-5x5)(9y8+15x5y4+25x10)
 | |||
 | |||
Пример: (2y-x)(4y2+2xy+x2)=8y3+4xy2+2x2y -4xy2 – 2x2y –x3
Теоремы об углах, образованных двумя параллельными прямыми и секущей (Доказательство теоремы 1)
Теоремы об углах, образованных двумя параллельными прямыми и секущей
(теоремы, обратные признакам параллельности прямых)
Теорема I
Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
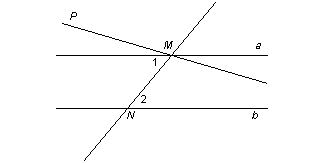 Дано: а || b, MN – секущая.
Дано: а || b, MN – секущая.
Доказать: 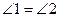 .
.
Доказательство:
Будем доказывать методом от противного.
I) Допустим, что 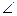 1 и
1 и 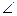 2 не равны, тогда построим
2 не равны, тогда построим 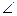 PMN =
PMN = 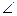 2.
2.
2) 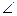 PMN и
PMN и 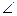 2 – накрест лежащие углы при прямых РМ и b,
2 – накрест лежащие углы при прямых РМ и b, 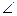 PMN =
PMN = 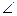 2, тогда по первому признаку параллельности прямых получим, что РМ || b.
2, тогда по первому признаку параллельности прямых получим, что РМ || b.
3) а || b (по условию).
РМ || b (по доказанному во 2).
Тогда получим, что через точку М проходит две прямые PM и a, параллельные прямой b, а это противоречит аксиоме параллельных.
Значит, наше предположение неверно, тогда 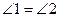 .
.
Что и требовалось доказать.
Теорема II
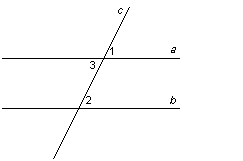 Если две параллельные прямые пересечены секущей, то соответственные углы равны.
Если две параллельные прямые пересечены секущей, то соответственные углы равны.
Дано: а || b, с – секущая.
Доказать: 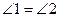 .
.
Доказательство:
1) 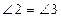 (по теореме I, т.к. а || b, с – секущая)
(по теореме I, т.к. а || b, с – секущая)
2) 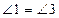 (т.к. вертикальные углы).
(т.к. вертикальные углы).
3) Из условий 1) и 2) получим, что 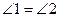 (если правые части равенств равны, то равны и левые).
(если правые части равенств равны, то равны и левые).
Что и требовалось доказать.
Теорема III
Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.
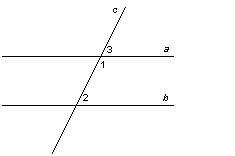 Дано: а || b, с – секущая.
Дано: а || b, с – секущая.
Доказать: 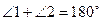 .
.
Доказательство:
1) 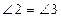 (по теореме II, т.к. а || b).
(по теореме II, т.к. а || b).
2) 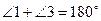 (т.к.
(т.к. 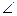 1 и
1 и 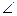 3 – смежные углы).
3 – смежные углы).
3) Подставим значение равенства (1) в равенство (2), получим: 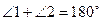 .
.
Что и требовалось доказать.
Следствия
Опр. Следствием называется утверждение, которое доказывается непосредственно из аксиом или теорем.
Следствие1 (из аксиомы параллельных прямых).
Если прямая пересекает одну из параллельных прямых, то она пересекает и другую прямую.
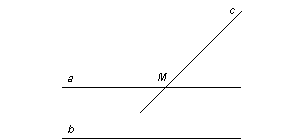 Дано: а || b, с
Дано: а || b, с  а = М.
а = М.
Доказать: с  b.
b.
Доказательство:
Будем доказывать методом от противного.
Предположим, что с и b не пересекаются, тогда с || b. Получим, что через точку М проходит две прямые а и с, параллельные прямой b. А это противоречит аксиоме параллельных прямых. Значит, наше предположение неверно. Тогда с  b.
b.
Что и требовалось доказать.
Следствие 2 (из теоремы I).
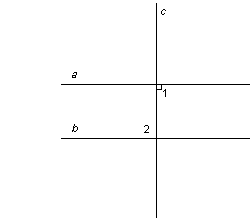 Если прямая перпендикулярна к одной из параллельных прямых, то она перпендикулярна и к другой прямой.
Если прямая перпендикулярна к одной из параллельных прямых, то она перпендикулярна и к другой прямой.
Дано: а || b, с 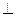 а.
а.
Доказать: с 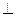 b.
b.
Доказательство:
1) 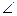 1 и
1 и 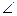 2 – накрест лежащие углыпри параллельных прямых а и b, секущей с, тогда по теореме 1
2 – накрест лежащие углыпри параллельных прямых а и b, секущей с, тогда по теореме 1 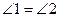 .
.
2) 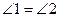 (по доказанному в 1).
(по доказанному в 1).
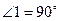 (по условию).
(по условию).
Отсюда 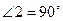 .
.
3) 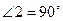 , тогда с
, тогда с  b.
b.
Что и требовалось доказать.
P.S.
1) Если две параллельные прямые пересечены секущей, то биссектрисы накрест лежащих углов параллельны.
2) Если две параллельные прямые пересечены секущей, то биссектрисы соответственных углов параллельны.
3) Если две параллельные прямые пересечены секущей, то биссектрисы односторонних углов перпендикулярны.
4) Если стороны одного угла соответственно параллельны сторонам другого угла, то такие углы или равны, или в сумме составляют 180°.