Вещества, которые намагничиваются в магнитном поле, называются магнетиками.

Занятие №34

Взаимодействие токов. Магнитный поток. Работа по перемещению проводника с током в магнитном поле.

 

Силы взаимодействия параллельных токов. Магнитная проницаемость среды.

Силы взаимодействия токов и магнитов в дальнейшем будем называть магнитными. Выясним, чем определяется сила взаимодействия двух параллельных токов (рис.1).

Если токи в проводниках I₁ и I₂ имеют одинаковые направления, то проводники притягиваются с равными по величине силами F₁ и F₂.

Наличие этих сил объясняется тем, что второй проводник находится в магнитном поле первого проводника, которое и создает силу F_2.

Очевидно, что сила F₁ в свою очередь создается магнитным полем второго проводника.

Изменяя силу тока в проводниках и расстояние а между ними, можно показать на опыте, что сила F действующая на отрезок l длинного провода, прямо пропорциональна произведению сил токов, длине l и обратно пропорциональна расстоянию a.

-сила взаимодействия проводников с током

Изменяя среду, в которой находятся проводники, можно установить, что сила зависит от окружающей среды. Следовательно, коэффициент пропорциональности K зависит как от выбора единиц измерения, так и от среды. Для упрощения ряда формул этот коэффициент

K= μ_с / 2π - в СИ

1)

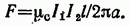
Здесь μ_с по-прежнему определяется выбором единиц измерения и свойствами среды.

Величину μ_с выражающую зависимость силы взаимодействия электрических токов от среды, называют магнитной проницаемостью среды.

Для силы взаимодействия токов в вакууме формулу можно записать в виде

2)

Здесь μ_о называется магнитной постоянной.

Если под F и F₀ подразумевать силы взаимодействия одних и тех же токов в какой-либо среде и в вакууме, то, разделив почленно (2) на (3), получим

3)

где μ относительная магнитная проницаемость среды — отвлеченное число. Относительная магнитная проницаемость показывает, во сколько раз сила взаимодействия токов в данной среде больше, чем в вакууме.

Опыты показали, что среда может как усиливать взаимодействие токов, так и ослаблять его по сравнению с вакуумом. Поэтому величина μ может быть как больше, так и меньше единицы. Числовое значение μ определяют опытным путем и при расчетах берут из таблиц.

Из (4) следует, что

 

Работа по перемещению проводника в магнитном поле. Магнитный поток.

Магнитным потоком называется часть магнитного поля, ограниченная замкнутым контуром.

f_(фи)= B∙S∙cosa - магнитный поток

A- угол между вектором

N (нормаль к площади контура) и В

S-площадь контура

Единица измерения в CИ:

f=1Тл∙1м²=1Тл∙м²=1Вб(Вебер)

Физический смысл: магнитный поток –есть общее число линий индукции магнитнго поля, пронизывающих площадь перпендикулярно поверхности и индукция В во всех точках поверхности одинакова.

 

 

 

А=F_A ∙b= В∙I∙l∙b = B 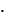I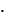∙ΔS B ΔS=B 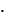S₂ – B S₁= Ф₂-Ф₁= ΔФ

A=I ΔФ -работа магнитного поля Δf=f₂-f₁-изменение магнитного поля.

Магнитные свойства вещества. Ферромагнетики и их применение

Вещества, которые намагничиваются в магнитном поле, называются магнетиками.

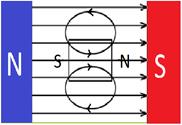
парамагнетики Молекулы имеют собственное магнитное поле     Внутри вещества происходит незначительное усиление магнитного поля µс ˃µo µ ˃1 Марганец, алюминий, азот

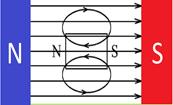
диамагнетики Молекулы не имеют собственного магнитного поля и намагничиваются во внешнем поле   Происходит незначительное ослабление магнитного поля внутри вещества µс ˂ µo µ ˂ 1 Вода, водород, висмут

ферромагнетики Вещества у которых магнитная проницаемость в 1000 раз больше µс, а µ намного больше 1 называется ферромагнетиками. Они могут усиливать внешние магнитные поля в 1000 раз Железо, сталь, чугун, кобальт и некоторые сплавы ферромагнитных металлов. Ферромагнетик состоит из множества самопроизвольно намагниченных областей размерами около 0.001мм, которые стали называть доменами. Стержень, который вставляют в соленоид, называют сердечником. Он служит для усиления магнитного поля. Применение: в электромагнитах, в амперметрах,вольтметрах, в трансформаторах,генераторах, электродвигателях.