Тема: Приложения дифференциального исчисления ФОП
К графику функции  в его точке с абсциссой
в его точке с абсциссой  проведена касательная. Тогда площадь треугольника, образованного касательной и отрезками, отсекаемыми ею на осях координат, равна …
проведена касательная. Тогда площадь треугольника, образованного касательной и отрезками, отсекаемыми ею на осях координат, равна …

| 
| ||
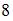
| |||

| |||
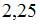
|
Решение:
Уравнение касательной к графику функции  в его точке с абсциссой
в его точке с абсциссой  имеет вид
имеет вид  . Вычислим последовательно
. Вычислим последовательно
 ,
, 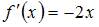 и
и 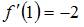 .
.
Тогда уравнение касательной примет вид
 .
.
Эта прямая пересекает оси координат в точках  и
и  , то есть отсекает на осях координат отрезки, длины которых равны 2 и 4. Следовательно, площадь соответствующего прямоугольного треугольника равна:
, то есть отсекает на осях координат отрезки, длины которых равны 2 и 4. Следовательно, площадь соответствующего прямоугольного треугольника равна:  .
.
Тема: Решение дифференциальных уравнений с помощью рядов
Три первых отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения  , удовлетворяющего начальным условиям
, удовлетворяющего начальным условиям  и
и  , имеют вид …
, имеют вид …

| 
| ||

| |||

| |||
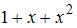
|
Тема: Типы дифференциальных уравнений
Уравнение  является …
является …

| уравнением с разделяющимися переменными | ||
однородным относительно  и и  дифференциальным уравнением первого порядка дифференциальным уравнением первого порядка
| |||
| линейным дифференциальным уравнением 1-го порядка | |||
| уравнением Бернулли |
Решение:
Данное уравнение можно представить в виде 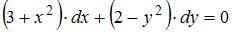 . Откуда
. Откуда 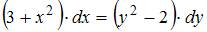 .
.
Следовательно, это уравнение является уравнением с разделяющимися переменными
Тема: Дифференциальные уравнения с разделяющимися переменными
Дифференциальное уравнение 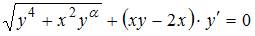 будет уравнением с разделяющимися переменными при значении
будет уравнением с разделяющимися переменными при значении 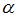 , равном …
, равном …

| |||
|
|
Решение:
Данное уравнение можно представить в виде  . Это уравнение будет уравнением с разделяющимися переменными при
. Это уравнение будет уравнением с разделяющимися переменными при  , то есть при
, то есть при  . Откуда
. Откуда  .
.
Тема: Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
Общее решение линейного однородного дифференциального уравнения второго порядка  имеет вид …
имеет вид …

| 
| ||

| |||

| |||

|
Тема: Типы дифференциальных уравнений
Уравнение  является …
является …

| однородным относительно  и и  дифференциальным уравнением первого порядка дифференциальным уравнением первого порядка
| ||
| линейным неоднородным дифференциальным уравнением первого порядка | |||
| уравнением Бернулли | |||
| дифференциальным уравнением с разделяющимися переменными |
Решение:
В уравнении  функция
функция  является однородной относительно
является однородной относительно  и
и  функцией нулевого порядка.
функцией нулевого порядка.
Действительно,  .
.
Поэтому данное уравнение является однородным относительно  и
и  дифференциальным уравнением первого порядка.
дифференциальным уравнением первого порядка.
Тема: Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
Частное решение 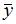 линейного неоднородного дифференциального уравнения второго порядка
линейного неоднородного дифференциального уравнения второго порядка  имеет вид …
имеет вид …

| 
| ||

| |||
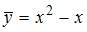
| |||

|
Тема: Дифференциальные уравнения с разделяющимися переменными
Дифференциальное уравнение  будет уравнением с разделяющимися переменными при значении
будет уравнением с разделяющимися переменными при значении 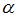 , равном …
, равном …

| |||
Решение:
Данное уравнение можно представить в виде  .
.
Это уравнение будет уравнением с разделяющимися переменными при 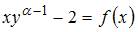 , то есть при
, то есть при  . Откуда
. Откуда  .
.
|
|
Тема: Приложения дифференциального исчисления ФОП
Максимум функции  равен …
равен …

| 
| ||

| |||
Решение:
Определим критические точки функции, для чего вычислим производную первого порядка  и решим уравнение
и решим уравнение  , а именно
, а именно  . Тогда
. Тогда  .
.
Определим производную второго порядка  и вычислим ее значения в критических точках:
и вычислим ее значения в критических точках:

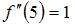 .
.
Так как 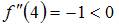 , то
, то  будет точкой максимума. Следовательно,
будет точкой максимума. Следовательно,  .
.
Тема: Решение дифференциальных уравнений с помощью рядов
Второй отличный от нуля член разложения в степенной ряд решения дифференциального уравнения  , удовлетворяющего начальному условию
, удовлетворяющего начальному условию  , будет равен …
, будет равен …

| 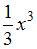
| ||

| |||

| |||

|
Решение:
Частное решение исходного уравнения, удовлетворяющее указанным начальным условиям, будем искать в виде ряда Маклорена: 
Из исходного уравнения находим, что  . Продифференцировав исходное уравнение, получим:
. Продифференцировав исходное уравнение, получим:  .
.
Тогда  .
.
Продифференцировав уравнение еще раз, получим 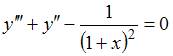 .
.
Следовательно,  .
.
Поэтому с учетом начальных условий имеем: 
Тема: Типы дифференциальных уравнений
Уравнение  является …
является …

| уравнением с разделяющимися переменными | ||
однородным относительно  и и  дифференциальным уравнением первого порядка дифференциальным уравнением первого порядка
| |||
| линейным дифференциальным уравнением 1-го порядка | |||
| уравнением Бернулли |
Решение:
Данное уравнение можно представить в виде 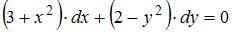 . Откуда
. Откуда 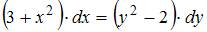 .
.
Следовательно, это уравнение является уравнением с разделяющимися переменными.
|
|
Тема: Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
Частное решение 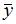 линейного неоднородного дифференциального уравнения второго порядка
линейного неоднородного дифференциального уравнения второго порядка  имеет вид …
имеет вид …

| 
| ||

| |||

| |||

|
Решение:
Общее решение этого уравнения можно записать в виде  , где функция
, где функция  – общее решение однородного уравнения
– общее решение однородного уравнения  , а функция
, а функция  – некоторое частное решение исходного неоднородного уравнения.
– некоторое частное решение исходного неоднородного уравнения.
Для однородного уравнения составим характеристическое уравнение 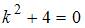 и найдем его корни:
и найдем его корни:  . Тогда общее решение однородного уравнения будет иметь вид
. Тогда общее решение однородного уравнения будет иметь вид  .
.
Поскольку правая часть исходного уравнения  , то имеем уравнение со специальной правой частью. Так как
, то имеем уравнение со специальной правой частью. Так как  не является корнем характеристического уравнения, то частное решение
не является корнем характеристического уравнения, то частное решение 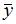 неоднородного уравнения будем искать в виде
неоднородного уравнения будем искать в виде  .
.
Подставим 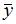 в исходное уравнение и найдем значения
в исходное уравнение и найдем значения 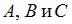 :
:  .
.
Следовательно, частное решение неоднородного уравнения  .
.
Тема: Дифференциальные уравнения с разделяющимися переменными
Общее решение дифференциального уравнения  имеет вид …
имеет вид …

| 
| ||
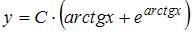
| |||
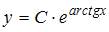
| |||

|
Тема: Приложения дифференциального исчисления ФОП
Промежуток возрастания функции 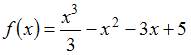 имеет вид …
имеет вид …

| 
| ||
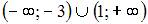
| |||

| |||
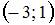
|
Решение:
Применим достаточное условие возрастания функции, которое можно сформулировать следующим образом: если в некотором промежутке  , то функция
, то функция  в этом промежутке возрастает. Поэтому вычислим производную первого порядка
в этом промежутке возрастает. Поэтому вычислим производную первого порядка  и решим неравенство
и решим неравенство  . Предварительно найдем корни уравнения
. Предварительно найдем корни уравнения  , а именно
, а именно  . Тогда
. Тогда  .
.
Следовательно,  при
при  .
.
Тема: Решение дифференциальных уравнений с помощью рядов
Три первых отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения  , удовлетворяющего начальным условиям
, удовлетворяющего начальным условиям  и
и  , имеют вид …
, имеют вид …

| 
| ||
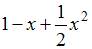
| |||

| |||

|
Решение:
Частное решение исходного уравнения, удовлетворяющее указанным начальным условиям, будем искать в виде ряда Маклорена: 
Из исходного уравнения находим, что  . Поэтому с учетом начальных условий имеем:
. Поэтому с учетом начальных условий имеем: 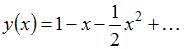
Тема: Приложения дифференциального исчисления ФОП
Уравнение касательной к графику функции  в его точке с абсциссой
в его точке с абсциссой  имеет вид …
имеет вид …

| 
| ||

| |||
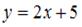
| |||

|
Решение:
Уравнение касательной к графику функции  в его точке с абсциссой
в его точке с абсциссой  имеет вид
имеет вид 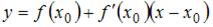 . Вычислим последовательно
. Вычислим последовательно
 ,
,  и
и  . Тогда уравнение касательной примет вид
. Тогда уравнение касательной примет вид
 , или
, или  .
.
Тема: Решение дифференциальных уравнений с помощью рядов
Три первых отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения  , удовлетворяющего начальным условиям
, удовлетворяющего начальным условиям  и
и  , имеют вид …
, имеют вид …

| 
| ||
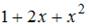
| |||

| |||

|
Решение:
Частное решение исходного уравнения, удовлетворяющее указанным начальным условиям, будем искать в виде ряда Маклорена: 
Из исходного уравнения  находим, что
находим, что  .
.
Поэтому с учетом начальных условий имеем: 
Тема: Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
Общий вид частного решения 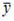 линейного неоднородного дифференциального уравнения второго порядка
линейного неоднородного дифференциального уравнения второго порядка 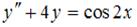 будет выглядеть как …
будет выглядеть как …

| 
| ||

| |||

| |||

|
Решение:
Общее решение этого уравнения можно записать в виде  , где функция
, где функция  – общее решение однородного уравнения
– общее решение однородного уравнения  , а функция
, а функция  – некоторое частное решение исходного неоднородного уравнения.
– некоторое частное решение исходного неоднородного уравнения.
Для однородного уравнения составим характеристическое уравнение  и найдем его корни:
и найдем его корни: 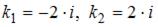 . Тогда общее решение однородного уравнения будет иметь вид
. Тогда общее решение однородного уравнения будет иметь вид  .
.
Поскольку правая часть исходного уравнения 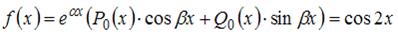 , то имеем уравнение со специальной правой частью. Так как
, то имеем уравнение со специальной правой частью. Так как  является корнем характеристического уравнения, то частное решение
является корнем характеристического уравнения, то частное решение  неоднородного уравнения будем искать в виде
неоднородного уравнения будем искать в виде  .
.
Тема: Дифференциальные уравнения с разделяющимися переменными
Если подкасательная в любой точке кривой равна удвоенной абсциссе точки касания, то уравнение этой кривой будет иметь вид …

| 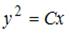 , , 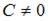
| ||
 , , 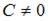
| |||

| |||
 , , 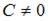
|
Тема: Типы дифференциальных уравнений
Уравнение  является …
является …

| линейным неоднородным дифференциальным уравнением первого порядка | ||
однородным относительно 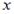 и и 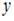 дифференциальным уравнением первого порядка дифференциальным уравнением первого порядка
| |||
| уравнением Бернулли | |||
| дифференциальным уравнением с разделяющимися переменными |
Тема: Решение дифференциальных уравнений с помощью рядов
Коэффициент при 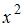 в разложении в степенной ряд решения дифференциального уравнения
в разложении в степенной ряд решения дифференциального уравнения 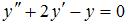 , удовлетворяющего начальным условиям
, удовлетворяющего начальным условиям 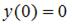 и
и  , будет равен …
, будет равен …

| – 1 | ||
| – 2 | |||
Решение:
Частное решение исходного уравнения, удовлетворяющее указанным начальным условиям, будем искать в виде ряда Маклорена: 
Из исходного уравнения находим, что  . Поэтому коэффициент при
. Поэтому коэффициент при  будет равен
будет равен 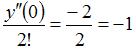 .
.
Тема: Типы дифференциальных уравнений
Уравнение  является …
является …

| уравнением Бернулли | ||
| линейным дифференциальным уравнением первого порядка | |||
| дифференциальным уравнением с разделяющимися переменными | |||
однородным относительно  и и  дифференциальным уравнением первого порядка дифференциальным уравнением первого порядка
|
Решение:
Уравнение  можно представить в виде
можно представить в виде  , где
, где  .
.
Действительно,  . Поэтому данное уравнение является уравнением Бернулли.
. Поэтому данное уравнение является уравнением Бернулли.
Тема: Дифференциальные уравнения с разделяющимися переменными
Если угловой коэффициент касательной к кривой в любой ее точке вдвое больше углового коэффициента радиуса-вектора точки касания, то уравнение этой кривой будет иметь вид …

|  , , 
| ||
 , , 
| |||

| |||
 , , 
|
Тема: Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
Общий вид частного решения  линейного неоднородного дифференциального уравнения второго порядка
линейного неоднородного дифференциального уравнения второго порядка  будет выглядеть как …
будет выглядеть как …

| 
| ||

| |||
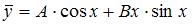
| |||

|
Решение:
Общее решение этого уравнения можно записать в виде  , где функция
, где функция  – общее решение однородного уравнения
– общее решение однородного уравнения  , а функция
, а функция  – некоторое частное решение исходного неоднородного уравнения.
– некоторое частное решение исходного неоднородного уравнения.
Для однородного уравнения составим характеристическое уравнение  и найдем его корни:
и найдем его корни:  . Тогда общее решение однородного уравнения будет иметь вид
. Тогда общее решение однородного уравнения будет иметь вид 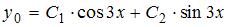 . Поскольку правая часть исходного уравнения
. Поскольку правая часть исходного уравнения 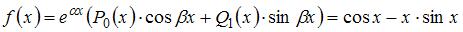 , то имеем уравнение со специальной правой частью. Так как
, то имеем уравнение со специальной правой частью. Так как  не является корнем характеристического уравнения, то частное решение
не является корнем характеристического уравнения, то частное решение  неоднородного уравнения будем искать в виде
неоднородного уравнения будем искать в виде  .
.
Тема: Приложения дифференциального исчисления ФОП
Наименьшее значение функции 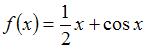 на отрезке
на отрезке 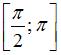 равно …
равно …

| 
| ||

| |||

| |||

|
Решение:
Вычислим производную первого порядка 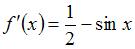 и решим уравнение
и решим уравнение 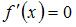 , а именно
, а именно  . Тогда
. Тогда 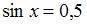 ,
, 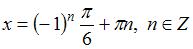 . Так как
. Так как  , то вычислим
, то вычислим
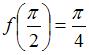 ,
,  ,
,  .
.
Тогда наименьшее значение данной функции равно  .
.
Тема: Решение дифференциальных уравнений с помощью рядов
Коэффициент при 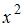 в разложении в степенной ряд решения дифференциального уравнения
в разложении в степенной ряд решения дифференциального уравнения 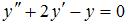 , удовлетворяющего начальным условиям
, удовлетворяющего начальным условиям 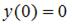 и
и  , будет равен …
, будет равен …

| – 1 | ||
| – 2 | |||
Решение:
Частное решение исходного уравнения, удовлетворяющее указанным начальным условиям, будем искать в виде ряда Маклорена: 
Из исходного уравнения находим, что  . Поэтому коэффициент при
. Поэтому коэффициент при  будет равен
будет равен 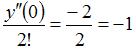 .
.
Тема: Приложения дифференциального исчисления ФОП
Промежуток возрастания функции  имеет вид …
имеет вид …

| 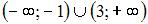
| ||

| |||

| |||

|
Решение:
Применим достаточное условие возрастания функции, которое можно сформулировать следующим образом: если в некотором промежутке  , то функция
, то функция 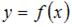 в этом промежутке возрастает. Поэтому вычислим производную первого порядка
в этом промежутке возрастает. Поэтому вычислим производную первого порядка 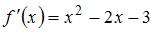 и решим неравенство
и решим неравенство  . Предварительно найдем корни уравнения
. Предварительно найдем корни уравнения 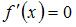 , а именно
, а именно 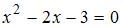 . Тогда
. Тогда  .
.
Следовательно,  при
при  .
.
Тема: Дифференциальные уравнения с разделяющимися переменными
Общее решение дифференциального уравнения 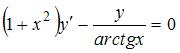 имеет вид …
имеет вид …

| 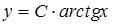
| ||

| |||

| |||

|
Решение:
Разделим переменные: 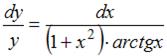 . Проинтегрируем обе части уравнения:
. Проинтегрируем обе части уравнения:  . Тогда
. Тогда  . Откуда
. Откуда 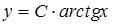 .
.
Тема: Типы дифференциальных уравнений
Уравнение 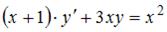 является …
является …

| линейным неоднородным дифференциальным уравнением первого порядка | ||
однородным относительно  и и  дифференциальным уравнением первого порядка дифференциальным уравнением первого порядка
| |||
| уравнением Бернулли | |||
| дифференциальным уравнением с разделяющимися переменными |
Решение:
Уравнение 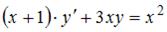 может быть сведено к уравнению вида
может быть сведено к уравнению вида  . Действительно,
. Действительно,  , поэтому данное уравнение является дифференциальным линейным уравнением первого порядка.
, поэтому данное уравнение является дифференциальным линейным уравнением первого порядка.
Тема: Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
Общий вид частного решения  линейного неоднородного дифференциального уравнения второго порядка
линейного неоднородного дифференциального уравнения второго порядка  будет выглядеть как …
будет выглядеть как …

| 
| ||

| |||

| |||

|
Тема: Приложения дифференциального исчисления ФОП
Промежуток убывания функции 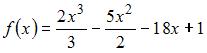 имеет вид …
имеет вид …

| 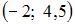
| ||
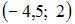
| |||
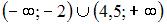
| |||
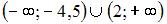
|
Решение:
Применим достаточное условие убывания функции, которое можно сформулировать следующим образом: если в некотором промежутке  , то функция
, то функция 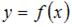 в этом промежутке убывает. Поэтому вычислим производную первого порядка
в этом промежутке убывает. Поэтому вычислим производную первого порядка  и решим неравенство
и решим неравенство  . Предварительно найдем корни уравнения
. Предварительно найдем корни уравнения 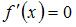 , а именно
, а именно  . Тогда
. Тогда  .
.
Следовательно,  при
при  .
.
Тема: Решение дифференциальных уравнений с помощью рядов
Два первых отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения  , удовлетворяющего начальным условиям
, удовлетворяющего начальным условиям  и
и  , имеют вид …
, имеют вид …