Задание
1. Хранящуюся в файле базу данных (БД) «Жизнь замечательных людей» загрузить в оперативную память компьютера, выполнить сортировку записей методом прямого слияния с использованием очередей. Построить индексный массив, провести поиск в упорядоченной базе по фамилии замечательных людей, используя в качестве ключа 3 первые буквы фамилии, из записей с одинаковым ключом сформировать очередь. Вывести содержимое очереди. Из записей очереди построить дерево оптимального поиска (приближенный алгоритм) по другому ключу (год издания книги) и произвести поиск по запросу.
2. При выполнении задания главное внимание следует уделить эффективности применяемых алгоритмов, исключению всех лишних операций.
3. Операции, выражающие логически завершенные действия, рекомендуется оформлять в виде подпрограмм, грамотно выбирая между процедурами и функциями. Имена переменных и подпрограмм, параметры подпрограмм, используемые языковые конструкции должны способствовать удобочитаемости программы.
4. Для сравнения символьных строк КАТЕГОРИЧЕСКИ НЕ РЕКОМЕНДУЕТСЯ пользоваться встроенными языковыми средствами и библиотечными функциями.
При работе с базой данных (БД) учесть следующие замечания:
1. Все текстовые поля следует pассматpивать как символьные массивы (array of char), а не стpоки (string). Это сделано для совместимости между языками Паскаль и Си, а также из-за того, что в базах данных не принято хранить лишнюю информацию, такую как длина строки. Если длина поля пpевышает pазмеp хpанимой в нем инфоpмации, то оно дополняется пpобелами спpава. Каждое текстовое поле имеет свой фоpмат, котоpый опpеделяет смысл записанных в него данных. Пpи описании фоpмата в угловых скобках < и > указываются отдельные его элементы (сами угловые скобки в состав текста не входят); пpобелы обозначаются с помощью символа подчеpкивания. Если поле включает только один текстовый элемент, то фоpмат не указывается.
2. Целочисленные поля пpедставляются 16-pазpядными положительными числами (типа word в Паскале).
3. Пpи описании стpуктуpы записей в пpогpаммах необходимо точно соблюдать поpядок и pазмеp полей.
Библиографическая БД «Жизнь замечательных людей» хранит записи следующей стpуктуpы:
Автоp: текстовое поле 12 символов
фоpмат <Фамилия>_<буква>_<буква>
Заглавие: текстовое поле 32 символа
фоpмат <Имя>_<Отчество>_<Фамилия>
Издательство: текстовое поле 16 символов
Год издания: целое число
Кол-во стpаниц: целое число
Пpимеp записи из БД:
Кловский_В_Б
Лев_Hиколаевич_Толстой_________
Молодая_гваpдия_
Постановка задачи
Согласно заданию программа должна последовательно выполнить следующие действия:
· загрузить в память все записи БД;
· выполнить сортировку записей методом прямого слияния с использованием очередей;
· построить индексный массив;
· выполнить поиск записей по ключу, введенному пользователем, с использованием массива и формированием очереди из найденных записей;
· вывести на экран результаты поиска, если это согласовано пользователем;
· построить массив, упорядоченный по году издания книг, необходимый для построения ДОП;
· построить ДОП по приближенному алгоритму А2;
· выполнить поиск в ДОП по ключу, введенному пользователем с выводом информации о количестве найденных изданий;
Кроме того, программа должна протоколировать результаты работы в файле журнала программы KR.LOG, создаваемого в каталоге с исполняемым файлом программы.
После выполнения перечисленных действий программа должна завершать работу.
Требования к подпрограммам, реализующим действия программы:
| Действие | Загрузка записей БД в оперативную память |
| Тип подпрограммы | Функция |
| Описание | Размещает в динамически создаваемых структурах, организованных в очередь, записи, последовательно считываемые из БД. |
| Входные параметры | нет |
| Выходные параметры | нет |
| Результат | указатель на созданную очередь |
| Действие | Сортировка очереди |
| Тип подпрограммы | Процедура |
| Описание | Сортирует очередь методом прямого слияния |
| Вх./вых. параметры | указатель на сортируемую очередь |
| Действие | Построение индексного массива |
| Тип подпрограммы | Функция |
| Описание | Распределяет динамическую память для размещения элементов массива в количестве, равном числу записей БД. Сохраняет в элементах массива адреса записей. |
| Входные параметры | указатель на отсортированную очередь |
| Выходные параметры | нет |
| Результат | указатель на созданный индексный массив |
| Действие | Поиск по ключу в упорядоченной БД |
| Тип подпрограммы | Функция |
| Описание | Последовательно перебирает элементы массива, сравнивает первые 3 символа названия книги с ключом, в случае совпадения сохраняет указатель на запись в динамически создаваемом элементе очереди результатов поиска. |
| Входные параметры | указатель на индексный массив |
| Выходные параметры | нет |
| Результат | указатель на созданную очередь или пустой |
| Действие | Вывод на экран очереди результатов поиска |
| Тип подпрограммы | Процедура |
| Описание | Последовательно перебирает элементы очереди, выводит на экран запись, адресуемую элементом очереди. При заполнении экрана запрашивает продолжение вывода, в случае подтверждения выводит следующий экран или остаток записей, в случае отказа – прекращает вывод. |
| Входные параметры | указатель на очередь результатов поиска |
| Выходные параметры | нет |
| Действие | Построение массива, упорядоченного по году издания книг |
| Тип подпрограммы | Функция |
| Описание | Обойти АВЛ-дерево слева направо, сохраняя в элементах массива указатели на вершины АВЛ-дерева. |
| Входные параметры | указатель на вершину АВЛ-дерева количество элементов массива |
| Выходные параметры | нет |
| Результат | указатель на созданный массив, упорядоченный по году издания книг, содержащий указатели на вершины АВЛ-дерева с рассчитанными весами |
| Действие | Построение АВЛ-дерева |
| Тип подпрограммы | Функция (вспомогательная) |
| Описание | Последовательно перебирая элементы очереди результатов поиска, добавить в АВЛ-дерево вершину, если год издания не найден в АВЛ-дереве, увеличить вес вершины, если год ее год совпадает с годом элемента очереди. |
| Входные параметры | указатель на вершину АВЛ-дерева, количество элементов массива |
| Выходные параметры | нет |
| Результат | указатель на корень АВЛ-дерева |
| Действие | Построение ДОП (алгоритм А2) |
| Тип подпрограммы | Функция |
| Описание | Добавлять вершины, адресуемые элементами массива, в соответствии с приближенным алгоритмом А2. |
| Входные параметры | указатель на массив вершин, упорядоченный по году издания книг, с рассчитанными весами |
| Выходные параметры | нет |
| Результат | указатель на корень ДОП |
| Действие | Поиск по ключу в ДОП с выводом информации о количестве найденных изданий |
| Тип подпрограммы | Функция |
| Описание | Спускаясь по ветвям ДОП, найти вершину с годом равным ключу. Вывести на экран вес вершины. |
| Входные параметры | указатель на корень ДОП, ключ поиска |
| Выходные параметры | нет |
| Результат | указатель на найденную вершину или пустой |
Основные алгоритмы
Сортировка последовательностей методом прямого слияния
В основе метода прямого слияния лежит операция слияния серий. р-серией называется упорядоченная последовательность из р элементов.
Пусть имеются две упорядоченные серии a и b длины q и r соответственно. Необходимо получить упорядоченную последовательность с, которая состоит из элементов серий a и b. Сначала сравниваем первые элементы последовательностей a и b. Минимальный элемент перемещаем в последовательность с. Повторяем действия до тех пор, пока одна из последовательностей a и b не станет пустой, оставшиеся элементы из другой последовательности переносим в последовательность с. В результате получим (q+r)-серию.
Пусть длина списка S равна степени двойки, т.е. 2k, для некоторого натурального k. Разобьем последовательность S на два списка a и b, записывая поочередно элементы S в списки а и b. Сливаем списки a и b с образованием двойных серий, то есть одиночные элементы сливаются в упорядоченные пары, которые записываются попеременно в очереди c0 и c1. Переписываем очередь c0 в список a, очередь c1 – в список b. Вновь сливаем a и b с образованием серий длины 4 и т. д. На каждом итерации размер серий увеличивается вдвое. Сортировка заканчивается, когда длина серии превысит общее количество элементов в обоих списках. Если длина списка S не является степенью двойки, то некоторые серии в процессе сортировки могут быть короче.
Трудоёмкость метода прямого слияния определяется сложностью операции слияния серий. На каждой итерации происходит ровно n перемещений элементов списка и не более n сравнений. Количество итераций равно 
. Тогда
C < n , M=n +n.
Дополнительные n перемещений происходят во время начального расщепления исходного списка. Асимптотические оценки для М и С имеют следующий вид
С=О(n log n), М=О(n log n) при n → ∞.
Метод обеспечивает устойчивую сортировку. При реализации для массивов, метод требует наличия второго вспомогательного массива, равного по размеру исходному массиву. При реализации со списками дополнительной памяти не требуется.
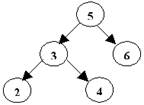
Обход дерева слева направо
При обходе дерева слева направо выполняется обход левого поддерева, корня, правого поддерева.
Результат обхода: 4 2 5 1 3 6.
Алгоритм на псевдокоде
Обход слева направо(p: pVertex)
IF(p 
NIL)
Обход слева направо (p 
Left)
Печать(p Data)
Обход слева направо (p Right)
FI
Приближенный алгоритм А2 построения ДОП
Дерево поиска, имеющее минимальную средневзвешенную высоту, называется деревом оптимального поиска (ДОП). Средневзвешенная высота дерева с n вершинами:
hср=(w1h1+w2h2+...+wnhn)/W, где
wn – вес вершины Vn,пропорциональный частоте ее поиска
hn – высота, на к-рой расположена вершина Vn
W – вес дерева (сумма весов всех вершин)
Алгоритм (А2) использует предварительно упорядоченный набор вершин. В качестве корня выбирается такая вершина, что разность весов левого и правого поддеревьев была минимальна. Для этого путем последовательного суммирования весов определяем вершину Vk, для которой справедливы неравенства:
, 
.
Тогда в качестве "центра тяжести" может быть выбрана вершина Vk, Vk-1 или Vk+1, т. е. вершина, для которой разность весов левого и правого поддерева минимальна. Далее действия повторяются для каждого поддерева.
Сложность алгоритма как функция от n (количество элементов) зависит следующим образом: время Т = О(n log n), память М = О(n) при n 
. (Время определяется трудоемкостью сортировки элементов, а память - размером массива для хранения элементов). Дерево, построенное приближенным алгоритмом А2, асимптотически приближается к оптимальному (с точки зрения средней высоты) при n .
Поиск вершины в дереве поиска
Двоичное дерево называется деревом поиска, если ключ в каждой его вершине больше ключа любой вершины в левом поддереве и меньше ключа любой вершины в правом поддереве, в дереве нет вершин с одинаковыми данными.
В основном деревья поиска используются для организации быстрого и удобного поиска элемента с заданным ключом во множестве данных, которое динамически изменяется. Приведенная ниже процедура поиска элемента в дереве поиска возвращает указатель на вершину с заданным ключом, в противном случае возвращаемое значение равно пустому указателю.
Алгоритм на псевдокоде
Поиск вершины с ключом Х
p: = Root
DO (p NIL)
IF(p Data < x) p:= p Right
ELSEIF (p Data >x) p: = p Left
ELSE
OD { p Data = x }
OD
IF (p NIL) <вершина найдена>
ELSE <вершина не найдена>
OD
Максимальное количество сравнений при поиске равно Сmax = 2h, где h высота дерева.
Построение АВЛ-дерева
Дерево поиска называется сбалансированным по высоте, или АВЛ-деревом, если для каждой его вершины высоты левого и правого поддеревьев отличаются не более чем на 1.
Добавление новой вершины в АВЛ-дерево происходит следующим образом. Вначале добавляем новую вершину в дерево так же как в случайное дерево поиска (проход по пути поиска до нужного места). Затем, двигаясь назад по пути поиска от новой вершины к корню дерева, ищем вершину, в которой нарушился баланс (т. е. высоты левого и правого поддеревьев стали отличаться более чем на 1). Если такая вершина найдена, то изменяем структуру дерева для восстановления баланса с помощью процедур поворотов:
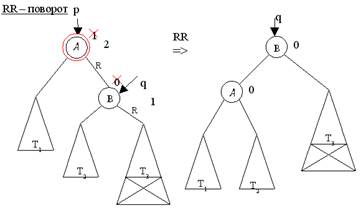
Адельсон - Вельский и Ландис доказали теорему, гарантирующую, что АВЛ-дерево никогда не будет в среднем по высоте превышать ИСДП более, чем на 45% независимо от количества вершин: log(n+1) 
hАВЛ(n) < 1,44 log(n+2) - 0,328 при n .
Поиск элемента с заданным ключом, включение нового элемента, удаление элемента - каждое из этих действий в АВЛ-дереве можно произвести в худшем случае за О(log n) операций.
Основные структуры данных
Запись БД tRow
Структура хранит информацию о книге, считанную из БД (автор, название, издатель, год издания, количество страниц).
tAuthor = array [1.. 12] of char;
tTitle = array [1.. 32] of char;
tPublisher = array [1.. 16] of char;
pRow = ^tRow;
tRow = record
Author: tAuthor;
Title: tTitle;
Publisher: tPublisher;
Year: Word;
PageCount: Word;
end;
Элемент очереди tQueueItem
Структура хранит указатели на следующую структуру tQueueItem и на структуру tRow.
pQueueItem = ^tQueueItem;
tQueueItem = record
Next: pQueueItem;
Data: pRow;
end;
Очередь tQueue
Структура хранит указатели на первую и последние структуры списка tQueueItem. Используется при загрузке БД в память, поиске в БД.
pQueue = ^tQueue;
tQueue = record
Head,
Tail: pQueueItem;
end;
Вершина дерева tVertex
Структура хранит указатели на левую и правую дочерние вернины, данные, вес и баланс. Используется при работе с ДОП и АВЛ-деревом.
pVertex = ^tVertex;
tVertex = record
Data: Word;
Weight: Word;
Balance: Integer;
Left,
Right: pVertex;
end;
Динамический массив tArrayOfpRow
Массив хранит указатели на структуры tRow. Используется при поиске в упорядоченной БД.
pArrayOfpRow = ^tArrayOfpRow;
tArrayOfpRow = array [1.. cMaxCount] of pRow;
Динамический массив tArrayOfpVertex
Массив хранит указатели на структуры tVertex. Используется при построении ДОП.
pArrayOfpVertex = ^tArrayOfpVertex;
tArrayOfpVertex = array [1.. cMaxCount] of pVertex;