Пример выполнения РГР №3

Исходные данные:

Рис. 3.1.

Решение.

1. Определить классическим методом переходное напряжение на емкости (для четных последних цифр шифра) или переходный ток в индуктивности (для нечетных последних цифр шифра). Характеристическое уравнение составить методом входного комплексного сопротивления.

Расчет проводим согласно следующему алгоритму.

1). Составление математической модели.

Рис. 3.2. Схема после коммутации для составления матмодели

Запишем три уравнения по законам Кирхгофа для мгновенных значений, учитывая компонентное уравнение ёмкости :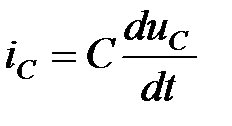

Выкладки становятся проще, если составить ДУ относительно напряжения на емкости. С этой целью в записанной системе уравнений нужно избавиться от тока до разветвления и тока в индуктивности.

Выражение для тока i ₁ из первого уравнения подставим во второе и преобразуем это уравнение:

где

Из преобразованного уравнения найдем выражение для тока в индуктивности, а затем – для его производной, учитывая, что E₀ = const:

Эти выражения подставим в третье уравнение исходной системы:

После преобразования этого уравнение получим окончательно неоднородное ДУ второго порядка:

или

Перейдем к приведенному ДУ:

Подсчитаем значения коэффициентов ДУ:

Итак, получена математическая модель в виде неоднородного ДУ второго порядка с постоянными коэффициентами:

Из этого уравнения можно получить два уравнения первого порядка (уравнения состояния). С этой целью напряжение на емкости назовем первой переменной состояния и обозначим через x₁, а ее первую производную назовем второй переменной состояния и обозначим через x₂, т.е.

Сразу же получено первое уравнение состояния:

Записав исходное ДУ в виде

получим второе уравнение состояния:

Запишем уравнения состояния в виде системы уравнений:

Для получения матриц уравнений состояния запишем первое уравнение со всеми переменными состояния и входным воздействием, т.е. ЭДС источника:

Матрицы уравнений состояния:

2). Нахождение начальных условий..

Начальными условиями (НУ) называются значения искомой переменной y(t) и ее n – 1 производных в момент коммутации, где n – порядок дифференциального уравнения, т.е. .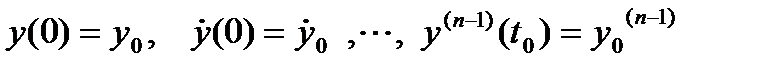

Схемы с незаряженными конденсаторами, которые включаются под напряжение, называются схемами включения. Такие схемы имеют нулевые независимые начальные условия, т.е. напряжения на емкостях и токи в индуктивностях таких схем равны нулю.

Таким образом, для схемы примера имеем:

Значения первых производных этих величин в момент коммутации, т.е. зависимые НУ, определяются в схеме после коммутации по законам Кирхгофа для мгновенных значений с использованием независимых начальных условий. Т.к. ток в ветви с индуктивностью в момент коммутации равен нулю, то индуктивность можно удалить из ветви. Т.к. напряжение на емкости в момент коммутации равно нулю, то ее можно закоротить. В результате получим схему для момента времени t = 0, в которой можно определить зависимые НУ:

Рис. 3.3. Схема для момента коммутации

Ток в емкости в момент коммутации:

Напряжение на индуктивности – это напряжение на выделенных зажимах удаленного элемента. Следовательно:

Отсюда получаем значение производной тока в индуктивности в момент коммутации:

Компонентное уравнение емкости позволяет определить значение производной напряжения на емкости в момент коммутации:

Выпишем начальные условия для искомых величин.

3). Составление характеристического уравнения, определение его корней и запись свободных составляющих переходных величин.

Решение неоднородного дифференциального уравнения состоит из суммы двух решений – общего решения однородного уравнения (свободная составляющая переходной величины) и частного решения неоднородного уравнения (принужденная составляющая). Например, для напряжения на емкости можно записать:

Для записи свободной составляющей нужно составить характеристическое уравнение. Его можно составить по дифференциальному уравнению n -го порядка. Для этого старшая производная переходной величины меняется на pⁿ, следующая производная – на p ⁿ^-1 и т.д., сама искомая величина заменяется единицей, коэффициенты остаются на своих местах, правая часть уравнения равна нулю. Так, для уравнения 2-го порядка получим характеристическое уравнение 2-ой степени:

Подставив значения коэффициентов, получим уравнение:

Характеристическое уравнение можно получить с помощью матрицы коэффициентов уравнений состояния по формуле

det (p E – A) = 0,

где E – единичная матрица.

Найдем матрицу p E – A:

Определитель этой матрицы:

Приравнивая этот определитель нулю, получаем то же характеристическое уравнение:

Итак, характеристическое уравнение составляется по дифференциальному уравнению или с помощью матрицы коэффициентов уравнений состояния. В тоже время есть еще один способ составления характеристического уравнения без математической модели. С этой целью используется комплексная схема замещения, для которой записывается выражение комплексного входного сопротивления. При этом комплексное сопротивление индуктивности записывается в виде Z _L = jωL, а комплексное сопротивление емкости – в виде . Затем вместо jω подставляется p, все выражение приводится к отношению двух полиномов и полином числителя приравнивается к нулю. Это и будет характеристическое уравнение. Рассмотрим применение этого способа к схеме данного примера. Комплексная схема замещения имеет вид:

Рис. 3.4. Схема для получения характеристического уравнения

Записываем выражение для входного комплексного сопротивления схемы

Производим замену j ω на p и преобразуем получение выражение к отношению двух полиномов относительно p:

= .

Приравнивая к нулю числитель, получим характеристическое уравнение:

=0.

Разделив слагаемые левой части на R₁, получим такое же выражение для характеристического уравнения, как и по ДУ второго порядка.

Корни характеристического уравнения :

; .

Т.к. корни – комплексно-сопряженные, то свободные составляющие переходных величин записываются в виде:

4). Определение принужденных составляющих переходных величин.

Принужденные составляющие – это напряжения и токи (числа или функции времени) в схеме после коммутации в установившемся режиме, т.е. после того, как свободная составляющая прекратит свое действие. Если ЭДС источника постоянна, то в установившемся режиме емкость не пропускает постоянный ток, а индуктивность не оказывает ему сопротивления. Поэтому для получения схемы с принужденными составляющими необходимо в схеме после коммутации разомкнуть емкости и закоротить индуктивности. Схема для этого случая приведена на рис.3.5:

Рис. 3.5. Схема для принужденных составляющих

Из схемы следует:

5). Нахождение постоянных интегрирования и запись переходных величин.

Решение линейного неоднородного ДУ любого порядка можно представить в виде суммы общего решения однородного ДУ (уравнения без правой части) и частного решения исходного неоднородного уравнения. В теоретической электротехнике общее решение называется свободной, а частное – принужденной составляющими. Запишем для каждой переходной величины соответствующие выражения.

а). Напряжение на емкости.

Обще решение неоднородного ДУ:

После подстановки начального условия получим одно алгебраическое уравнение. Этого уравнения недостаточно для нахождения двух постоянных интегрирования. Поэтому для получения второго уравнения продифференцируем выражение для учитывая, что const:

;

Теперь в два последних выражения подставим начальные условия, т.е. в правых частях вместо t подставляем ноль, а в левых – значения напряжения и его первой производной в момент коммутации.

Выведем формулы для постоянных интегрирования в общем виде:

Найдем значения постоянных интегрирования для напряжения на емкости:

Теперь можно окончательно записать выражение для переходного напряжения на емкости:

или

б). Ток в индуктивности.

Постоянные интегрирования найдем по выведенным выше формулам:

Следовательно:

2). Построить временную диаграмму переходной величины с момента коммутации и до момента практического затухания переходного процесса

Построение выполняем в программе MathAD.

Постоянная времени огибающей затухающей синусоиды:

Построим также график свободной составляющей напряжения на емкости с двумя огибающими:

3. Закоротить емкость или индуктивность и определить переходный ток на входе схемы операторным методом, используя закон Ома в операторной форме. Оригинал искомого тока определить двумя способами: а) по теореме разложения; б) путем разложения изображения тока на простые дроби.

1). Закорочена емкость.

Т.к. ток в индуктивности в момент коммутации равен нулю (согласно первому закону коммутации), то операторная схема замещения не содержит источника внутренней ЭДС и имеет вид:

Рис. 3.6.

Операторное входное сопротивление схемы:

Ток на входе операторной схемы (изображение переходного тока):

Знаменатель операторного тока имеет два корня, один из которых нулевой:

Разложим изображение тока на сумму простых дробей:

Для нахождения коэффициентов K₁ и K₂ приведем правую часть к общему знаменателю и отбросим знаменатели обеих частей:

Приравняем коэффициенты при p и свободные члены:

В результате решения этих уравнений получим:

Следовательно, изображение тока можно представить в виде:

Применяя к каждому слагаемому формулы обратного преобразования Лапласа, получим оригинал:

Воспользуемся также теоремой разложения, которая для изображения, записанного в виде

записывается следующим образом:

В этом выражении p_k – корни уравнения , а – производная функции 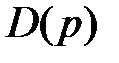по оператору p.

В данном примере уравнение имеет один корень:

p₁ = –39,4 c ^-1.

Т.к. то Кроме того: N (0) = 25,8; D (0) = 39,4;

Поэтому выражение для оригинала принимает вид:

2). Закорочена индуктивность.

Т.к. напряжение на емкости в момент коммутации равна нулю (согласно второму закону коммутации), то операторная схема замещения не содержит источника внутренней ЭДС и имеет вид: